PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN ỨNG HÒA
(Đề thi gồm 01 trang)
KIỂM TRA RÀ SOÁT CHẤT LƯỢNG
HỌC SINH LỚP 9 CHUẨN BỊ THI VÀO LỚP 10
THPT NĂM HỌC 2024-2025 ĐỢT 2
ĐỀ THI MÔN TOÁN
(Thời gian làm bài 120 phút, không kể thời gian giao đề)
Câu I. (2,0 điểm). Cho hai biểu thức:
A =
7
8
x
x
+
+
và B =
8 24
9
3
xx
x
x
+
−−
−
(với x
0; x
9)
1/ Tính giá trị biểu thức A khi x = 4.
2/ Rút gọn biểu thức B.
3/ Cho P = A.B. Tìm giá trị nhỏ nhất của
P
.
Câu II. (2,0 điểm).
1/ Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một ca nô xuôi dòng trên một khúc sông dài 90 km rồi ngược dòng về 63 km. Biết
thời gian xuôi dòng ít hơn thời gian ngược dòng là 1 giờ và vận tốc khi xuôi dòng hơn
vận tốc ngược dòng là 6km/h. Tính vận tốc ca nô lúc xuôi dòng và lúc ngược dòng.
2/ Một hình nón có bán kính đáy bằng 5cm và diện tích xung quanh là 65
π
cm2.
Tính thể tích của khối nón đó (làm tròn kết quả đến chữ số thập phân thứ hai).
Câu III. (2,5 điểm).
1/ Giải hệ phương trình:
2/ Trong hệ tọa độ Oxy, cho parabol (P): y = x2 và đường thẳng (d): y = 2mx + 3.
a. Tìm các điểm nằm trên parabol (P) có tung độ bằng 4.
b. Tìm m để (d) cắt (P) tại hai điểm phân biệt A và B sao cho SAOB = 6 (đvdt).
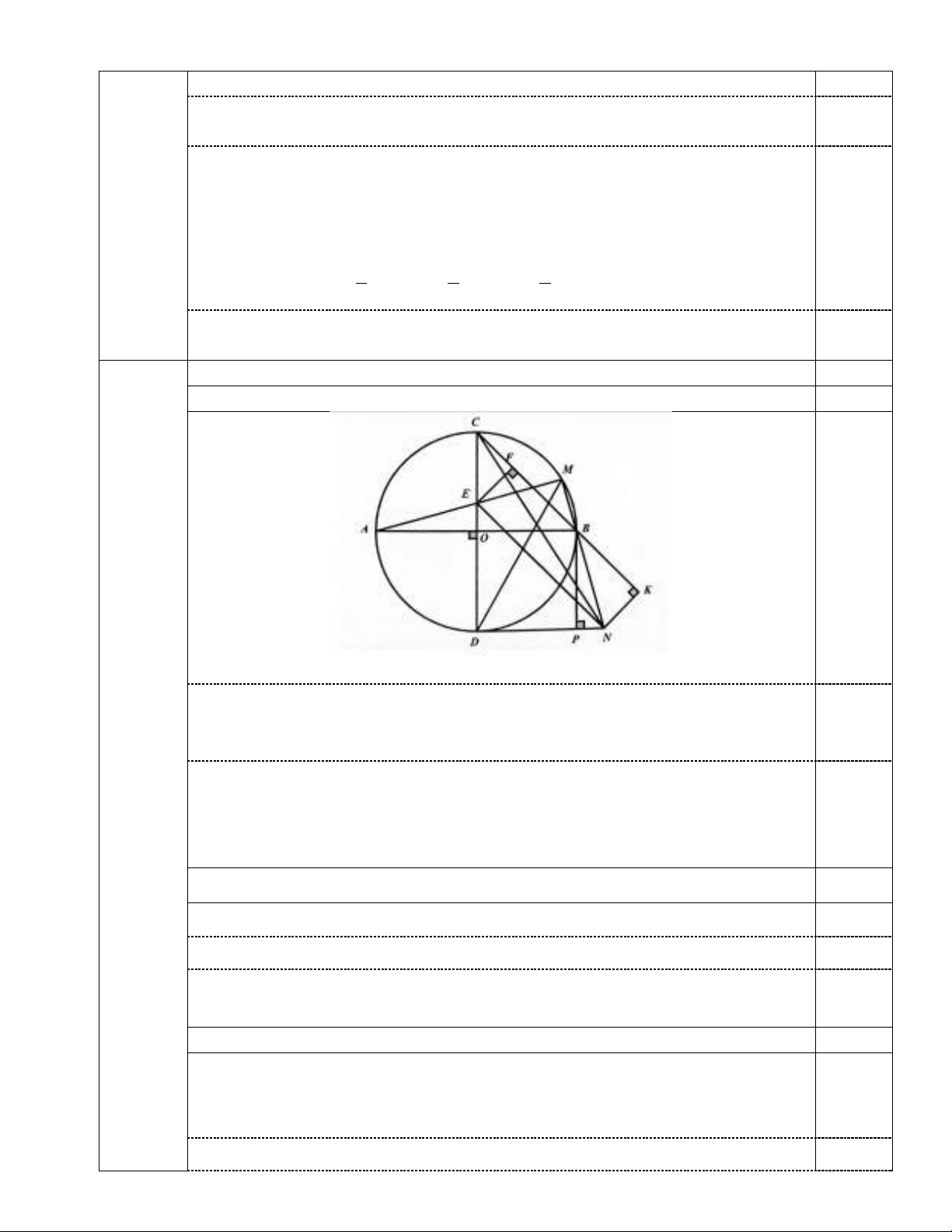
Câu IV. (3,0 điểm). Cho đường tròn (O; R) hai đường kính AB và CD vuông góc với
nhau. Lấy điểm M thuộc cung nhỏ BC, AM cắt CD tại E. Qua D kẻ tiếp tuyến với đường
tròn (O) cắt đường thẳng BM tại N. Gọi P là hình chiếu vuông góc của B trên DN.
1/ Chứng minh bốn điểm M, N, D, E cùng nằm trên một đường tròn.
2/ Chứng minh: EN// CB.
3/ Chứng minh AM.BN = 2R2 và tìm vị trí M trên cung nhỏ BC để diện tích
BNC
đạt giá trị lớn nhất.
Câu V. (0,5 điểm). Cho các số a; b; c không âm thỏa mãn a + b + c = 1. Chứng minh
rằng: T =
2025 2024 2023 1a b c ab bc ca+ + − − −
.
Họ và tên thí sinh:……………………………......…SBD:……………
ĐỀ CHÍNH THỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN ỨNG HÒA
KIỂM TRA RÀ SOÁT CHẤT LƯỢNG
HỌC SINH LỚP 9 CHUẨN BỊ THI VÀO LỚP
10 THPT NĂM HỌC 2024-2025 ĐỢT 2
HƯỚNG DẪN CHẤM MÔN TOÁN
Câu
ĐÁP ÁN
ĐIỂM
Câu I
(2 điểm)
1) Tính giá trị biểu thức
0,5
Thay x = 4 (tmđk) vào biểu thức A =
7
8
x
x
+
+
4 7 11 11
2 8 10
48
A+
= = =
+
+
0,25
Vậy khi x = 4 thì giá trị biểu thức A =
11
10
0,25
2) Chứng minh B
1,0
B =
8 24
9
3
xx
x
x
+
−−
−
(với x
0; x
9)
=
8 24
3 ( 3)( 3)
xx
x x x
+
+
− − +
0,25
=
( 3) 8 24
( 3)( 3)
x x x
xx
+ + +
−+
0,25
=
11 24
( 3)( 3)
xx
xx
++
−+
0,25
=
( 3)( 8) 8
( 3)( 3) 3
x x x
x x x
+ + +
=
− + −
0,25
3) Tìm giá trị nhỏ nhất của
P
0,5
+ Ta có P =
7 8 7 7
.
8 3 3 3
x x x x
P
x x x x
+ + + +
= =
+ − − −
P
có nghĩa khi
70 3 0 9
3
xxx
x
+ −
−
(vì x + 7 > 0 )
0,25
+ Xét
7 16 16
3 3 6
3 3 3
x
P x x
x x x
+
= = + + = − + +
− − −
(với
30x−
16
2 ( 3). 6 2.4 6 14 14
3
xP
x
− + = + = =
−
Dấu “=” xảy ra khi
2
16
( 3) ( 3) 16 3 4 49
3
x x x x
x
− = − = − = =
−
Vậy giá trị nhỏ nhất
14P=
khi x = 49
0,25
Câu II
(2,0
điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
1,5
+ Gọi vận tốc ca nô khi xuôi dòng là: x (km/h) ( Điều kiện: x > 6)
0,25
+ Thì vận tốc của ca nô khi ngược dòng là x – 6 (km/h)
0,25
+ Thời gian ca nô đi xuôi dòng và đi ngược dòng lần lượt là:
0,25
90
x
( giờ) và
63
6x−
(giờ)
Vì thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng 2 giờ nên ta có phương
trình:
63 90 1
6xx
−=
−
0,25
+ Đưa pt về: x2 +21x - 540 = 0; giải được x1 = 15 (tm); x2=-36(L)
0,25
Vậy vận tốc của ca nô khi xuôi dòng là 15 km/h; ngược dòng là 9 km/h
0,25
2) Tính thể tích khối nón:
0,5
+ Cho biết: r = 5cm; Sxq = 65
cm2;
Tính V = ?
+ Áp dụng công thức tính diện tích xung quanh hình nón:
Sxq =
65
.r.l 13
.r 5.
xq
S
l

= = =
(cm)
Theo định lý Pitago:
2 2 2 2
13 5 12h l r= − = − =
(cm)
+ Thể tích khối nón là:
22
11
. . . . .5 .12 100 314,16
33
V r h
= = =
(cm3)
Vậy thể tích của khối nón xấp xỉ 314,16 (cm3)
0,25
0,25
Câu III
(2,5
điểm)
1) Giải hệ phương trình…
Giải hệ phương trình:
23 1 7
1
52 3 1 4
1
y
x
y
x
+ − =
+
− − =
+
1,0
Đk:
1
1; 3
xy −
Đặt
1
1
31
a
x
yb
=
+
−=
0,25
Ta có hệ phương trình
2 7 2
...
5 2 4 3
a b a
a b b
+ = =



− = =

0,25
Thế vào ta được
1
11
212
1210
3 1 9
3 1 3 3
x
x
x
yy
y
=−
=+=
+
−= =
−=
(tmđk)
0,25
Vậy hệ phương trình có nghiệm (x; y) =
1 10
;
23

−


0,25
2) Cho parabol (P) và đường thẳng (d)…
1,5
a) Tìm các điểm nằm trên (P) có tung độ bằng 4.
0,5
+ Điểm M(xM; 4) thuộc (P)
22
42
M
M
M
x
xx
=
=
=−
0,25
+ Vậy hai điểm cần tìm là (2; 4) và (-2; 4)
0,25
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt A và B sao cho SAOB = 6 (đvdt).
1,0
+ Ta có phương trình hoành độ giao điểm (d) và (P) là:
0,25
x2 = 2mx + 3 x2 – 2mx – 3 = 0 (*)
+ Vì a.c = 1.(-3) < 0 => phương trình (*) có hai nghiệm phân biệt với mọi m.
Vậy (d) luôn cắt (P) tại hai điểm phân biệt cố hoành độ x1, x2 với mọi m
0,25
+ Theo hệ thức Vi-et
12
12
2
. 3 0
x x m
xx
+=
= −
Ta có tích x1.x2 trái dấu => A(x1; y1) và B(x2; y2) nằm về hai phía trục tung
Giao điểm của (d) và Oy là E(0;3). Gọi H, K là hình chiếu của A,B lên Oy
12
1 1 1
. . . . .3.(| x | | x |) 6
2 2 2
AOB AOE EOB
S S S OE AH OE BK= + = + = + =
0,25
+ Ta có: |x1| + |x2| = 4 (x1 + x2)2 – 2x1x2 + 2|x1x2| = 16
4m2 – 2.(–3) + 2.|–3| = 16 m2 = 1 m =
1
0,25
Câu IV
(3,0 điểm)
Hình học
3,0
1) Chứng minh bốn điểm M, N, D, E cùng thuộc một đường tròn.
1,0
Vẽ hình đúng đến ý 1
0,25
Lập luận được
0
90AMB =
( góc nội tiếp chắn nửa đường tròn)
0
90EMN=
0
90 ODN =
(vì DN là tiếp tuyến của đường tròn)
0
90EDN
=
0,25
0,25
Xét tứ giác MNDE ta có:
0
180EMN EDN
+=
Mà hai góc ở vị trí đối nhau .
Suy ra tứ giác MNDE là tứ giác nội tiếp đường tròn đường kính EN.
Hay bốn điểm M, N, D, E cùng thuộc một đường tròn đường kính EN.
0,25
2) Chứng minh EN// CB
0,75
Xét tứ giác nội tiếp MNDE có
DEN DMN=
(cùng chắn cung DN)
0,25
Xét đường tròn (O; R) có
DMN DCB=
(góc nội tiếp cùng chắn cung DB)
0,25
=>
OCB DEN=
mà hai góc này ở vị trí đồng vị
=> EN // CB
0,25
3) Chứng minh AM.BN = R2. Tìm vị trí điểm M để SBNC đạt GTLN
1,25
* Chứng minh: AM.BN = R2
//
AB CD AB DN
DN CD
⊥
⊥
ABM DNM=
(đồng vị) hay
ABM PNB=
0,25
Xét
ABM và
BNP có
0
90AMB BPN==
;
ABM PNB=
(cmt)
0,25

ABM và
BNP đồng dạng
..
AM AB AM BN AB BP
BP BN
= =
Nhận thấy tứ giác BPDO là hình vuông nên BP = OD = R
Do đó AM.BN = AB.BP = 2.2R = 2R2
0,25
* Tìm vị trí điểm M…
Kẻ NK
⊥
BC tại K; EF
⊥
BC tại F. Ta có
1..
2
NBC
S NK BC
=
Do BC không đổi nên
max NKmax
NBC
S
0,25
Mà ENKF là hình chữ nhật NKmax EFmax
E O M B
0,25
Bài V
(0,5 điểm)
Cho các số a; b; c không âm thỏa mãn a + b + c = 1. Chứng minh rằng:
T =
2025 2024 2023 1a b c ab bc ca+ + − − −
0,5
Ta có:
, , 0
1
abc
abc
+ + =
nên
0 , , 1 ( 1)( 1)( 1) 0a b c a b c − − −
( ) 1 1
11
abc ab bc ca a b c
a b c ab bc ca abc
− + + + + + −
+ + − − − −
0,25
Vì
0 , , 1abc
nên
2025 2024 2023
;;a a b b c c
1T a b c ab bc ca + + − − −
Dấu “=” xảy ra khi (a; b; c) = (1; 0; 0) hoặc (0; 1; 0) hoặc (0; 0; 1)
0,25
Khi chấm thi lưu ý:
- Điểm toàn bài để lẻ đến 0,25.
- Các câu hoặc các ý có cách làm khác hướng dẫn ở trên nếu đúng vẫn được điểm tối đa của câu hay ý đó.
- Bài IV: Thí sinh vẽ sai hình trong phạm vi câu nào thì không có điểm câu đó.