SỞ GD & ĐT QUẢNG TRỊ KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2018
TRƯỜNG THPT TX QUẢNG TRỊ Bài thi: TOÁN
ĐỀ THI THỬ LẦN 1 Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Họ, tên thí sinh:………………………………………………………
Số báo danh:………………………………………………………….
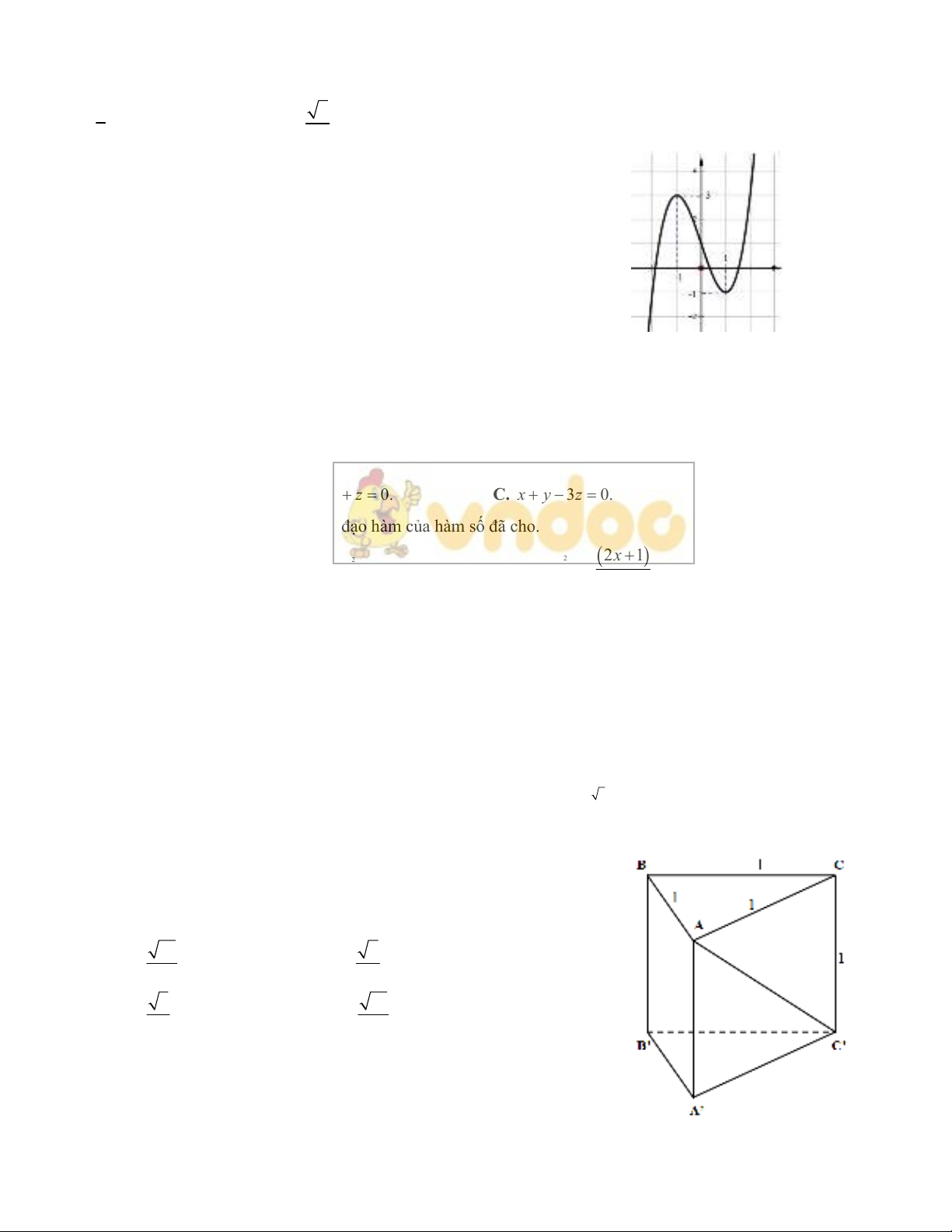
Câu 1. Cho hàm số
yfx liên tục trên có bảng biến
thiên như hình vẽ. Giá trị cực đại của hàm số là
A. 1.x B. 1.x
C. 4.y D. 0.y
Câu 2. Trong không gian với hệ toạ độ ,Oxyz cho đường thẳng d có phương trình tham số:
32
.
1
x
t
yt
zt


Đường
thẳng d có một vec-tơ chỉ phương là
A.
2;1; 1 .u
B.
3; 0;1 .u
C.
2;0; 1 .u
D.
3;1; 1 .u
Câu 3. Cho khối hộp chữ nhật .'' ' '
A
BCD A B C D có độ dài ,,'.
A
BaADbAA c
Thể tích của khối hộp chữ
nhật đã cho bằng
A. .
6
abc B. .abc C. .
3
abc D. .
4
abc
Câu 4. Cho hình phẳng
H giới hạn bởi đồ thị các hàm số
,yfxygx và các đường thẳng ,
x
ax b
,ab trong đó
yfx và

ygx là các hàm số liên tục trên đoạn

;.ab Diện tích của hình phẳng
H
được tính theo công thức
A.
 
.
b
a
Sfxgxdx

B.
 
22
.
b
a
Sfxgxdx

C.
 
.
b
a
Sfxgxdx
D.
 
22
.
b
a
Sfxgxdx
Câu 5. Phương trình đường tiệm cận ngang của đồ thị hàm số 21
1
x
yx
là
A. 2.y B. 1.
2
x C. 1.x D. 1.y
Câu 6. Cho số phức z có điểm biểu diễn trong mặt phẳng toạ độ là điểm
2; 1 .M Mô-đun của số phức z bằng
A. 3. B. 3. C. 5. D. 5.
Câu 7. Phương trình cos 1
x
có tập nghiệm là
A.
;.Skk
 B. 2; .
2
Skk




C.
2; .Sk k
 D. ;.
2
Skk




Câu 8. Có bao nhiêu cách xếp 3 bạn ,,
A
BC
vào một dãy ghế hàng ngang có 4 chỗ ngồi?
A. 4 cách. B. 24 cách. C. 6 cách. D. 64 cách.
Câu 9. Nghiệm của phương trình

4
log 1 3x là
A. 66.x B. 63.x C. 68.x D. 65.x
Trang 1/6 – Mã đề thi 234
Mã đề thi 234
Câu 10. Trong không gian với hệ toạ độ ,Oxyz cho điểm
2;1;0M và mặt phẳng
:2230.Px y z
Khoảng cách từ điểm
M
đến mặt phẳng

P
bằng
A. 1.
3 B.
3.
3 C. 3. D. 1.
Câu 11. Hình bên là đồ thị của hàm số nào trong các hàm số sau?
A. 331.yx x
B. 331.yx x
C. 32
31.yx x
D. 32
31.yx x
Câu 12. Cho hình nón
N có chiều cao 4,h bán kính đường tròn đáy 3.r Diện tích xung quay của hình nón
N bằng
A. 12 .
B. 20 .
C. 15 .
D. 30 .
Câu 13. Trong không gian với hệ toạ độ ,Oxyz cho hai điểm
1;1; 2A và
0; 2;3 .B Mặt phẳng

P
đi qua
gốc toạ độ và vuông góc với đường thẳng đi qua hai điểm ,AB
có phương trình là
A. 20.xyz
B. 0.xyz C. 30.xy z D. 350.xyz
Câu 14. Cho hàm số 22
7.
xx
y
Tính đạo hàm của hàm số đã cho.
A.

22
'7 2 1ln7.
xx
yx


B.

22
'7 2 1.
xx
yx


C.
2221
'7 .
ln 7
xx x
y
D. 22
'7 ln7.
xx
y
Câu 15. Trong không gian với hệ toạ độ ,Oxyz cho ba điểm
1; 2; 1 , 2; 1; 3AB và

3; 5;1 .C Gọi điểm
;;D abc thoả mãn tứ giác
A
BCD là hình bình hành. Tính tổng .Tabc
A. 1.T B. 5.T C. 3.T D. 1.T
Câu 16. Cho hàm số 32
22yx x
có đồ thị

C và điểm
1;1M thuộc

.C Gọi là tiếp tuyến của

C tại
.
M
Đường thẳng đi qua điểm nào sau đây?
A.
0; 2 .P C.
3; 0 .Q C.
3; 0 .R D.

0; 2 .S
Câu 17. Cho các số thực ,ab
đồng thời thoả mãn 3 2 1152
ab và
5
log 2.ab
Tính giá trị của biểu thức
.Pab
A. 9.P B. 3.P C. 8.P D. 6.P
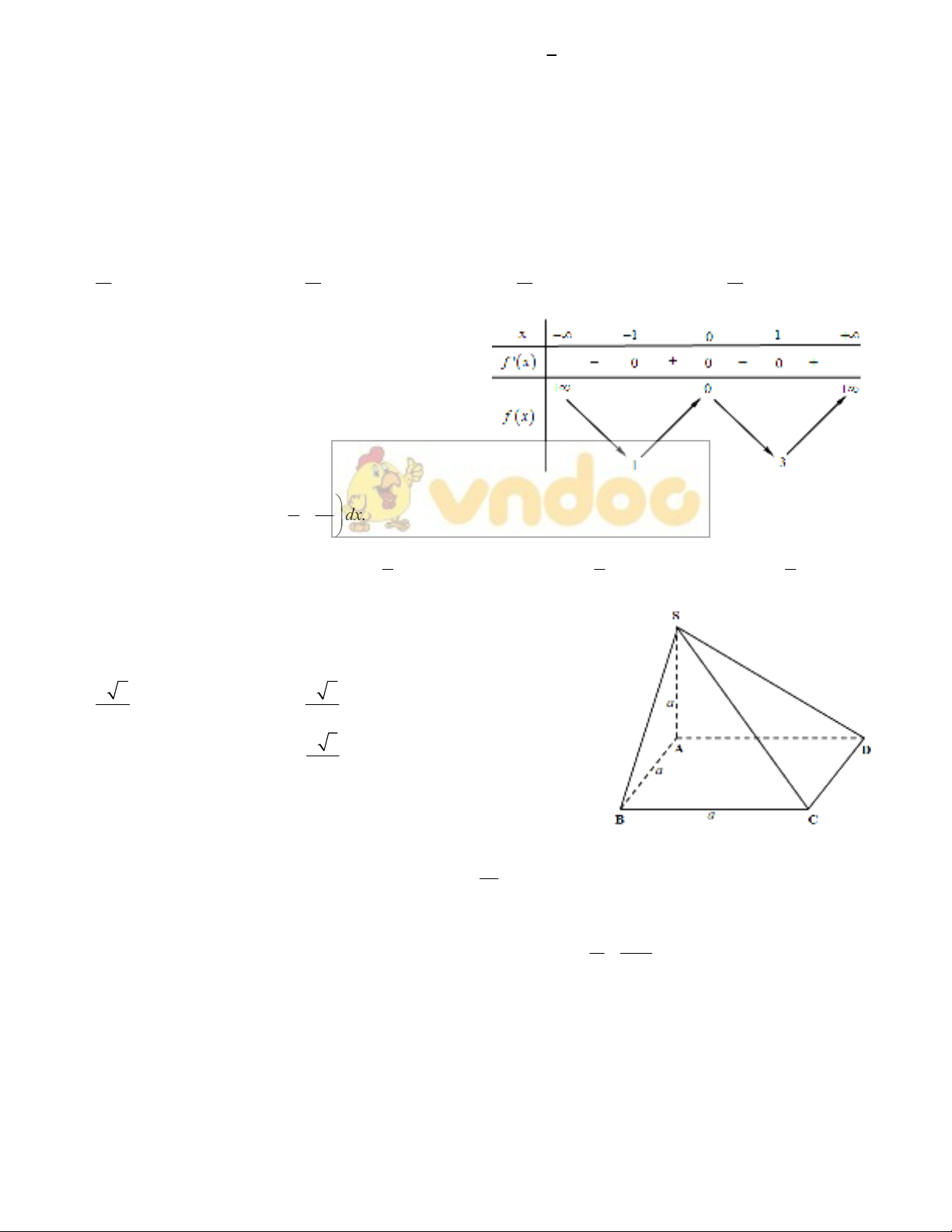
Câu 18. Cho hình lăng trụ đều .'' '
A
BC A B C có tất cả các cạnh đều bằng 1
(tham khảo hình vẽ). Gọi
là góc hợp bởi đường thẳng '
A
C với mặt phẳng
''.
B
CC B Tính sin .
A. 10
sin .
4
B. 6
sin .
4
C. 3
sin .
4
D. 13
sin .
4
Trang 2/6 – Mã đề thi 234
Câu 19. Tìm tất cả các giá trị thực của tham số m để hàm số

32
123
3
y
xmx m x
có đúng hai điểm cực
trị.
A.
;2 1; .m B.
1; 2 .m C.

;1 2; .m D.
2;1 .m
Câu 20. Kí hiệu 12
,zz
là các nghiệm phức của phương trình 2
2370.zz
Tính giá trị của 1212
zz.Sz z
A. 2.S B. 2.S C. 5.S D. 5.S
Câu 21. Để kiểm tra chất lượng sản phẩm của một công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp sữa
cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp sữa để đem đi phân tích mẫu.
Xác suất để 3 hộp được chọn có đủ cả 3 loại sữa bằng
A. 3.
11 B.
8.
11 C.
1.
11 D.
6.
11
Câu 22. Cho hàm số
yfx liên tục trên và có
bảng biến thiên như hình vẽ. Phương trình
1fx có
tất cả bao nhiêu nghiệm thực?
A. 4. B. 3.
C. 1. D. 2.
Câu 23. Tính tích phân
2
2
1
21 .Idx
xx

A. 1.I B. 1
2ln2 .
2
I
C. 1
2ln2 .
2
I
D. 1
2.
2
Ie
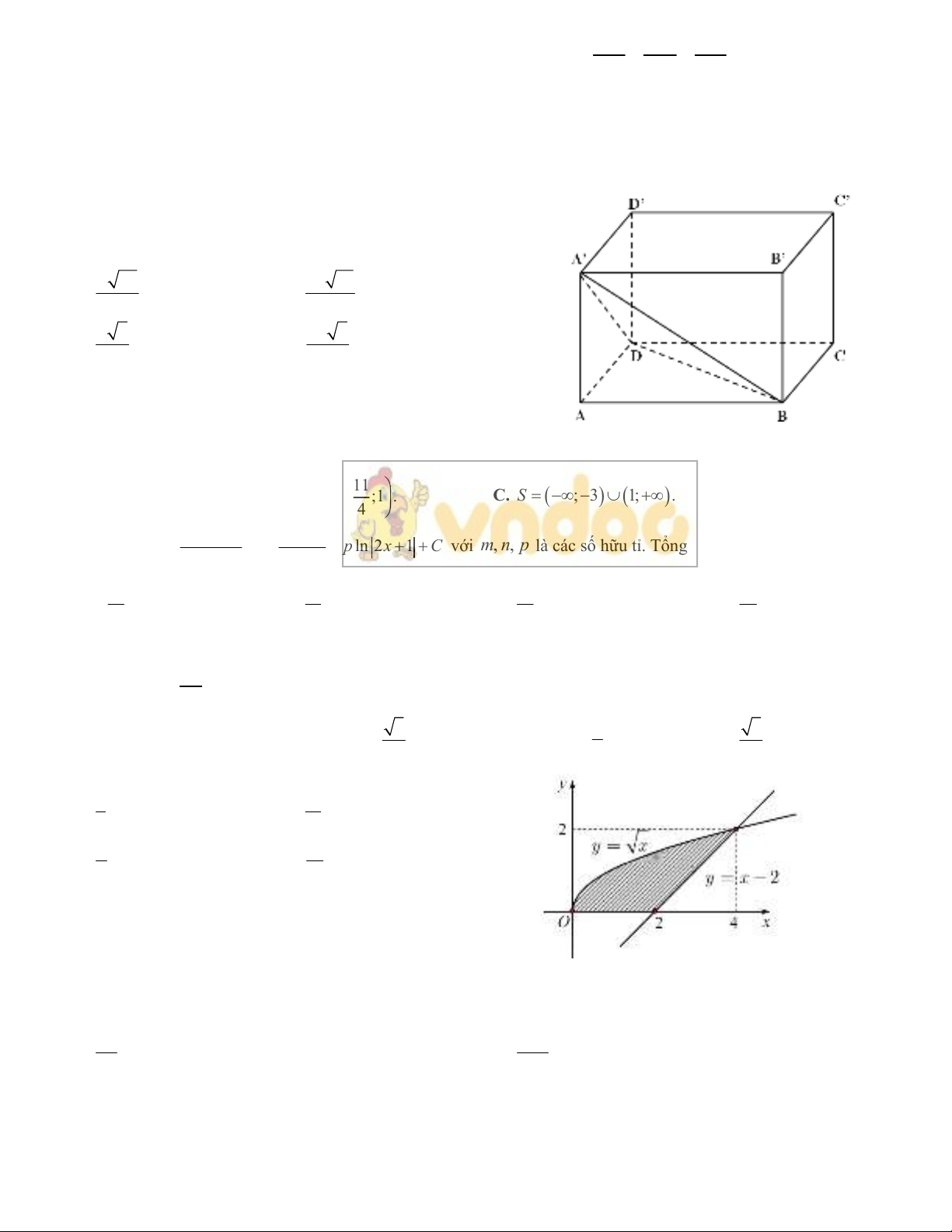
Câu 24. Cho hình chóp .SABCD
có đáy
A
BCD là hình vuông cạnh ,a
cạnh bên SA vuông góc với mặt phẳng đáy và SA a (tham khảo hình
vẽ). Khoảng cách từ đường thẳng
A
B đến mặt phẳng
SCD bằng
A. 2.
2
a B. 6.
3
a
C. .a D.
3.
2
a
Câu 25. Tìm số hạng không chứa
x
trong khai triển
9
2
8.xx



A. 43008. B. 43008. C. 32086. D.
32086.
Câu 26. Có bao nhiêu giá trị nguyên của tham số m để phương trình 40
41
m
xx

có nghiệm

0; 4 ?x
A. 7. B. 6. C. 4. D. 8.
Câu 27. Trong không gian với hệ toạ độ ,Oxyz cho điểm
2;1;1I và mặt phẳng

:2 2 1 0.Pxyz Phương
trình mặt cầu
S có tâm
I
và tiếp xúc với mặt phẳng

P
là
A.

222
2114.xyz
B.

222
2112.xyz
C.

222
2114.xyz
D.

222
2112.xyz
Trang 3/6 – Mã đề thi 234
Câu 28. Trong không gian với hệ toạ độ ,Oxyz cho đường thẳng 111
:21 1
xy
z

và mặt phẳng

:
P
30.xyz Gọi d là đường thẳng nằm trong

,
P
đi qua giao điểm của và

,
P
đồng thời vuông góc với
. Giao điểm của đường thẳng d với mặt phẳng toạ độ
Oxy là
A.

2; 2; 0 .M B.

3; 2; 0 .M C.

1; 4; 0 .M D.

3; 4; 0 .M
Câu 29. Cho hình hộp đứng .'' ' '
A
BCD A B C D có mặt đáy
A
BCD
là hình thoi cạnh
0
,60,a BAD cạnh bên '
A
Aa (tham khảo hình
vẽ). Khoảng cách từ điểm 'C đến mặt phẳng
'
A
BD bằng
A. 21 .
7
a B. 221
.
7
a
C. 5.
5
a D. 25
.
5
a
Câu 30. Bất phương trình


2
0,4 0,4
log 4 11 log 6 8xxx
có tập nghiệm là
A.

3;1 .S B. 11;1 .
4
S

C.
;3 1; .S D.

2;1 .S
Câu 31. Biết

2
22 1 ln 2 1
21
xdx p x C
mx n
x

với ,,mn p
là các số hữu tỉ. Tổng mn p bằng
A. 11.
2
B. 11.
2 C.
13.
2 D.
13.
2
Câu 32. Tìm tất cả giá trị thực của tham số m để phương trình
2
cos 1 cos 2 cos sin
x
xm x m x có đúng hai
nghiệm 2
0; .
3
x



A. 01.m
B. 3
1.
2
m C. 1
1.
2
m D. 31.
2m
Câu 33. Diện tích hình phẳng được tô đậm ở hình bên bằng
A. 8.
3 B.
11.
3
C. 7.
3 D. 10 .
3
Câu 34. Cho hình chóp tam giác .SABC
có 1, 2, 2SA SB SC
đồng thời các đường thẳng ,,SA SB SC đôi một
vuông góc. Thể tích của khối cầu ngoại tiếp hình chóp .SABC
bằng
A. 9.
2
B. 9.
C.
27 .
2
D. 27 .
Câu 35. Cho bất phương trình
22
log 5 log 1 log 4 ,
x
mx x m m
là tham số thực. Có bao nhiêu giá trị
nguyên của tham số m để bất phương trình nghiệm đúng với mọi ?x
A. 3. B. 2. C. 0. D. 1.
Trang 4/6 – Mã đề thi 234
Câu 36. Cho hàm số

2
3 khi 1.
4 khi 1
xx
yfx xx


Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi đồ thị hàm số
,yfx trục hoành và các đường thẳng 0, 2xx
quanh trục hoành bằng
A. 29 .
4 B. 29 .
4
C. 122 .
15 D. 122 .
15
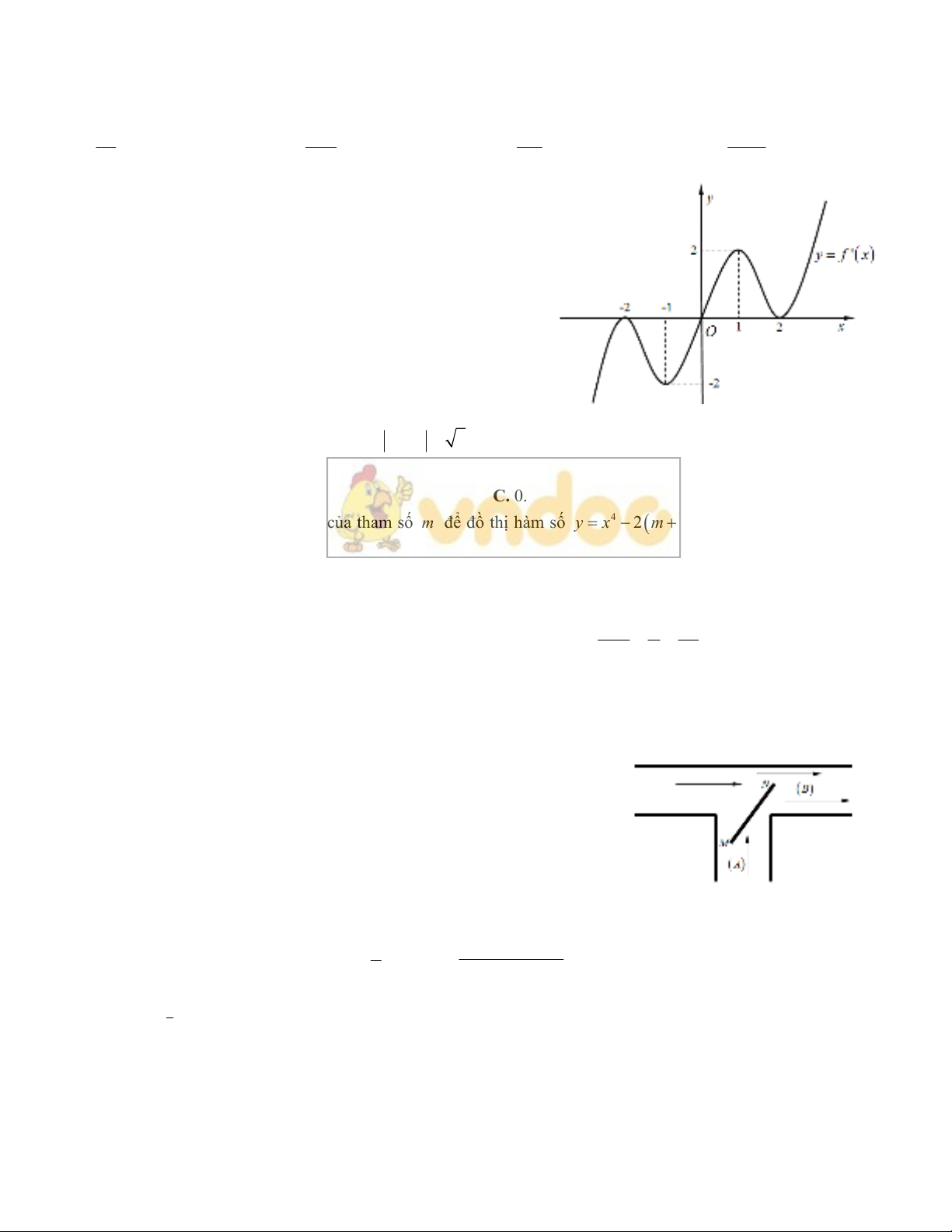
Câu 37. Cho hàm số
yfx có đạo hàm liên tục trên và có
đồ thị hàm số
'yfx như hình vẽ. Hàm số

2
2yfx x
có
bao nhiêu điểm cực trị?
A. 4. B. 5.
C. 3. D. 1.
Câu 38. Có bao nhiêu số phức z thoả mãn 25zi và tập điểm biểu diễn của số phức z trong mặt phẳng toạ
độ là đường thẳng :3 1 0?xy
A. 2. B. 1. C. 0. D. Vô số.
Câu 39. Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số
42
21yx m x m có ba điểm cực trị
,,
A
BC
sao cho ;OA BC trong đó O là gốc toạ độ,
A
là điểm cực trị trên trục tung và ,
B
C là hai điểm cực trị
còn lại. Tích của tất cả các phần tử trong tập S bằng
A. 8. B. 8. C. 4. D. 4.
Câu 40. Trong không gian với hệ toạ độ ,Oxyz cho đường thẳng 1
:212
xy
z
d
và hai điểm
2;1; 0 ,A
2;3; 2 .B Gọi
S là mặt cầu đi qua hai điểm ,
A
B và có tâm thuộc đường thẳng .d Diện tích của mặt cầu
S
bằng
A. 68 .
B. 25 .
C. 74 .
D. 26 .
Câu 41. Có hai mương nước

A
và

B
thông nhau, bờ của mương nước

A
vuông góc với bờ của mương nước

B, chiều rộng của hai mương
nước bằng nhau và bằng 8 mét (tham khảo hình vẽ). Một khúc gỗ
M
N có bề
dày không đáng kể trôi từ mương nước

A
sang mương nước

B theo
dòng chảy. Độ dài lớn nhất của khúc gỗ bằng bao nhiêu để nó có thể trôi lọt?
(tính gần đúng đến chữ số phần trăm).
A. 22,63 mét. B. 22,61 mét. C. 23,26 mét. D. 23,62 mét.
Câu 42. Cho dãy số
n
u thoả mãn 1
2
3
u và
 
11.
22 1 1
n
n
n
u
un
nu

 Tìm số nguyên dương n nhỏ nhất
thoả mãn 1
2
log 12,3.
n
u
A. 50.n B. 60.n C. 51.n D. 61.n
Câu 43. Trong không gian với hệ toạ độ ,Oxyz có bốn điểm
0;1; 2 , 1; 1; 0 , 0; 2;1AB C và
1; 0; 1 .D Có
bao nhiêu mặt cầu đi qua cả bốn điểm ,,, ?ABCD
A. 3. B. 1. C. 0. D. Vô số.
Trang 5/6 – Mã đề thi 234