së GD & ®t qu¶ng b×nh kú thi tuyÓn sinh vµo líp 10 thpt
n¨m häc 2012 - 2013
(ĐỀ CHÍNH THỨC) Khoá ngày 04 - 07 - 2012
Môn : TOÁN
Họ tên : ........................ Thời gian làm bài : 120 phút (không kể thời gian giao đề)
SBD: ............................ MÃ ĐỀ: 011
Đề thi gồm có 01 trang
Câu 1: (2,0 điểm) Cho biểu thức 2
1 2 1
1
A
x x x x
a) Rút gọn biểu thức A.
b) Tìm tất cả các giá trị nguyên của x để biểu thức A có giá trị nguyên.
Câu 2: (1,5 điểm) Giải hệ phương trình sau:
3 3
2 7
x y
x y
Câu 3: (2,0 điểm)
a) Giải phương trình: 2
2 3 0
.
b) Cho phương trình bậc hai: 2
2 0
x x m
(m là tham số).
Tìm m để phương trình có hai nghiệm x1, x2 và thoả mãn: 2 2
1 2
8
x x
.
Câu 4: (1,0 điểm) Cho các số thực a, b thoả mãn:
2
a b
.
Tìm giá trị nhỏ nhất của biểu thức:
3 3 2 2
P a b a b
.
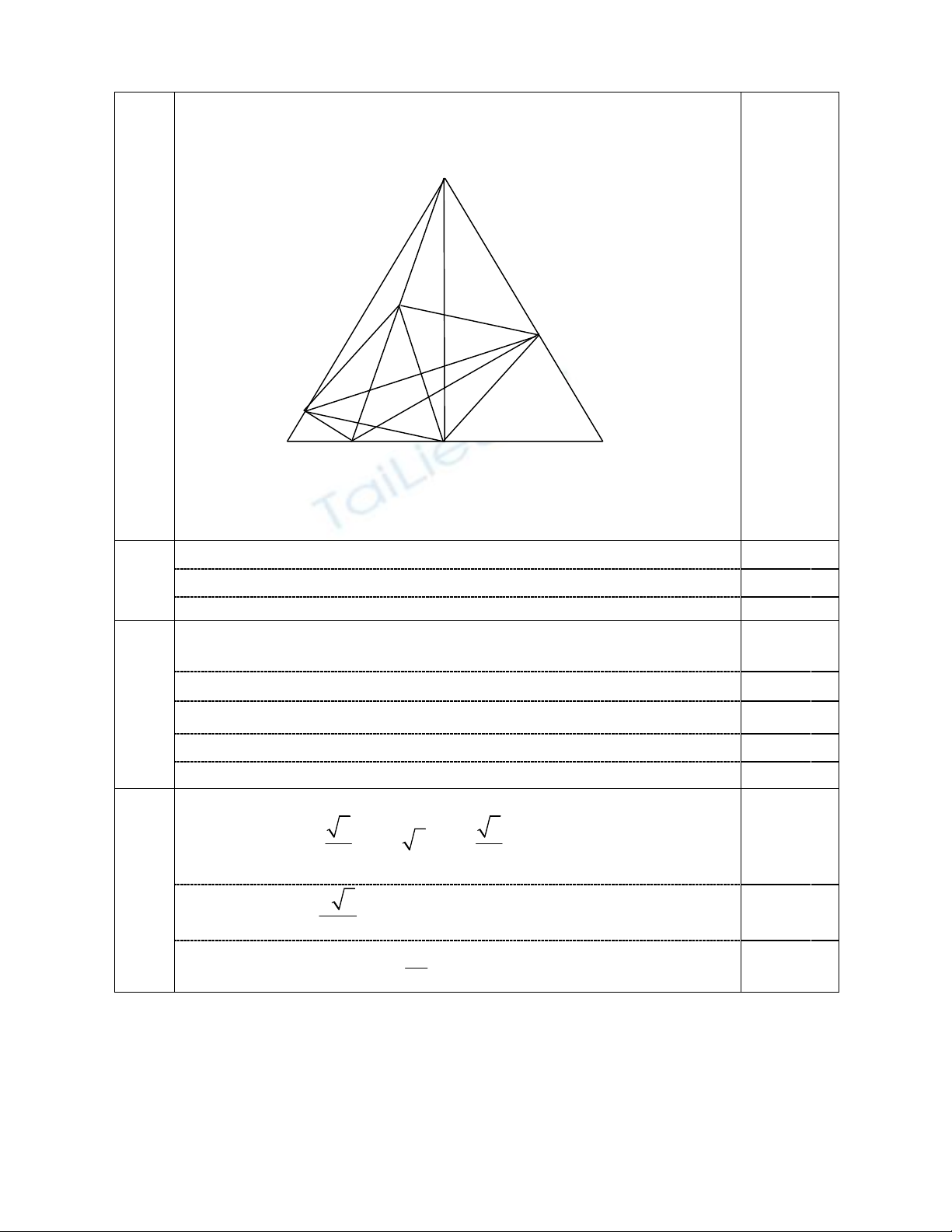
Câu 5: (3,5 điểm) Cho tam giác ABC đều có AH là đường cao, M là điểm bất kì trên
cạnh BC (M khác B, C). Từ M vẽ MP vuông góc AB, MQ vuông góc AC (P thuộc
AB, Q thuộc AC).
a) Chứng minh: A, P, M, H, Q cùng nằm trên một đường tròn.
b) Gọi O là trung điểm của AM. Chứng minh các tam giác OPH và OQH là tam
giác đều, từ đó suy ra
OH PQ
.
c) Tìm giá trị nhỏ nhất của đoạn PQ khi M chạy trên cạnh BC, biết độ dài cạnh của
tam giác ABC là a.
HÕT
Mã đề 011 - 013 Trang 1
HƯỚNG DẪN VÀ ĐÁP ÁN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2012 - 2013
Khóa ngày 04 - 07 - 2012
Môn: TOÁN
MÃ ĐỀ: 011-013
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết, rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những
bước giải sau có liên quan.
* Điểm thành phần của mỗi câu nói chung phân chia đến 0.25 điểm. Đối với điểm
thành phần là 0.5 điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0.25 điểm.
* Học sinh không vẽ hình đối với Câu 5 thì cho điểm 0 đối với Câu 5. Trường hợp học
sinh có vẽ hình, nếu vẽ sai ở ý nào thì cho điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm
của từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu.
Câu
Nội dung
Điểm
1
2,0 điểm
1a
Cho biểu thức 2
1 2 1
1
A
x x x x
ĐK:
0
x
và
1
x
0,25
1 2 1
1
x x
Ax x
0,25
3
1
x
x x
0,25
3
1
x
0,25
1b
3
1
A
x
với
0
x
và
1
x
0,25
A có giá trị nguyên khi x - 1 là ước nguyên của 3. 0,25
1 3 2
1 1 0 (lo¹i)
1 1 2
1 3 4
x x
x x
x x
x x
0,25
Vậy biểu thức A có giá trị nguyên khi
2; 2
x x
và
4
x
0,25
2
1,5 điểm
3 3
(I)
2 7
x y
x y
Mã đề 011 - 013 Trang 2
Cộng từng vế hai phương trình của (I) ta được:
5 10
y
0,5
2
y
0,25
Do đó, ta có
3 3 3
( )
2 2
x y x
Iy y
0,5
Vậy hệ phương trình có nghiệm duy nhất
; 3;2
x y . 0,25
Lưu ý: Học sinh chỉ viết kết quả thì cho 0,75 điểm
3 2,0 điểm
3a
Phương trình: 2
2 3 0
.
Ta có
1 2 3 0
a b c . 0.5
Phương trình có hai nghiệm
1; 3
x x
0,5
Lưu ý: Học sinh chỉ viết kết quả thì cho 0,5 điểm
3b
Để phương trình 2
2 0
x x m
có hai nghiệm x1, x2 khi và chỉ
khi
2
' 0 1 0 1
m m
0,25
Theo định lí Viet 1 2 1 2
2,
x x x x m
0,25
2
2 2
1 2 1 2 1 2
2
8 2 8
2 2 8
m = 2 (tho¶ m·n)
x x x x x x
m
0,25
0,25
Vậy với
2
m
phương trình có hai nghiệm x1, x2 và thoả m
ãn:
2 2
1 2
8
x x
.
4 1,0 điểm
Ta có
3 2
3 2
P a b ab a b a b ab
12 8 ( 2)
ab do a b
2
12 8 2
8 16 12
a a
a a
0,25
0,25
2
8 1 4 4, aa
0,25
P = 4 khi và chỉ khi 2
( 1) 0
1
2
a
a b
a b
Vậy giá trị nhỏ nhất của P là 4 khi a = b = 1
0,25
5 3,5 điểm
Mã đề 011 - 013 Trang 3
Hình vẽ
0,5
5a Ta có:
MP AB
,
MQ AC
,
AH BC
0,25
Nên: P, H, Q cùng nhìn đoạn AM dưới một góc vuông 0,5
Vậy A, P, M, H, Q cùng nằm trên đường tròn đường kính AM 0,25
5b
Xét đường tròn đường kính AM, tâm O.
Ta có: OP = OH = OQ nên
, HOQ
POH
cân tại O 0,25
0
® 2 ® 60
s POH s PAH
0,25
0
® 2 ® 60
s HOQ s HAQ 0,25
Suy ra
, HOQ
POH
đều
OP PH HQ QO
0,25
Do đó tứ giác OPHQ là hình thoi
OH PQ
0,25
5c
Gọi I là giao điểm của OH và PQ.
3 3
2 2. 3
2 2
PQ PI OP OA AM
0,25
Mà
3
2
a
AM AH . 0,25
Vậy giá trị nhỏ nhất PQ là
3
4
a
khi M trùng H. 0,25
A
B C
H
M
P
Q
O
I