Trang 1/28 - Mã đề thi 157
TRƯỜNG THPT ………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
157
Họ và tên:………………………………………….Lớp:……………...……..………
Câu 1. Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
có các cạnh bên hợp với đáy những góc bằng
0
60
, đáy
ABC
là tam giác đều cạnh
a
và
'A
cách đều
, ,A B C
. Tính khoảng cách giữa hai đáy của hình lăng
trụ.
A.
3
2
a. B.
. C.
a
. D.
2
a.
Lời giải
Chọn C
Ta có:
( ' ' ') / /( )A B C ABC
(( ' ' '),( )) ( ',( ))d A B C ABC d A ABC
.
Gọi
M
là trung điểm
BC
. Gọi
H
là trọng tâm tam giác
ABC
.
Tam giác
ABC
đều, trọng tâm
H
và
'A
cách đều
, ,A B C
.
Suy ra:
'A
thuộc trục đường tròn ngoại tiếp tam giác
ABC
' ( )A H ABC
( ',( )) 'd A ABC A H
.
Mặt khác: góc giữa cạnh bên và đáy bằng
0
60
0
' 60
A AH .
Trong tam giác
'A AM
: 0 0
' 2 3
tan 60 ' .tan 60 . . 3
3 2
A H a
A H AH a
AH
.
Suy ra: (( ' ' '),( ))
d A B C ABC a
.
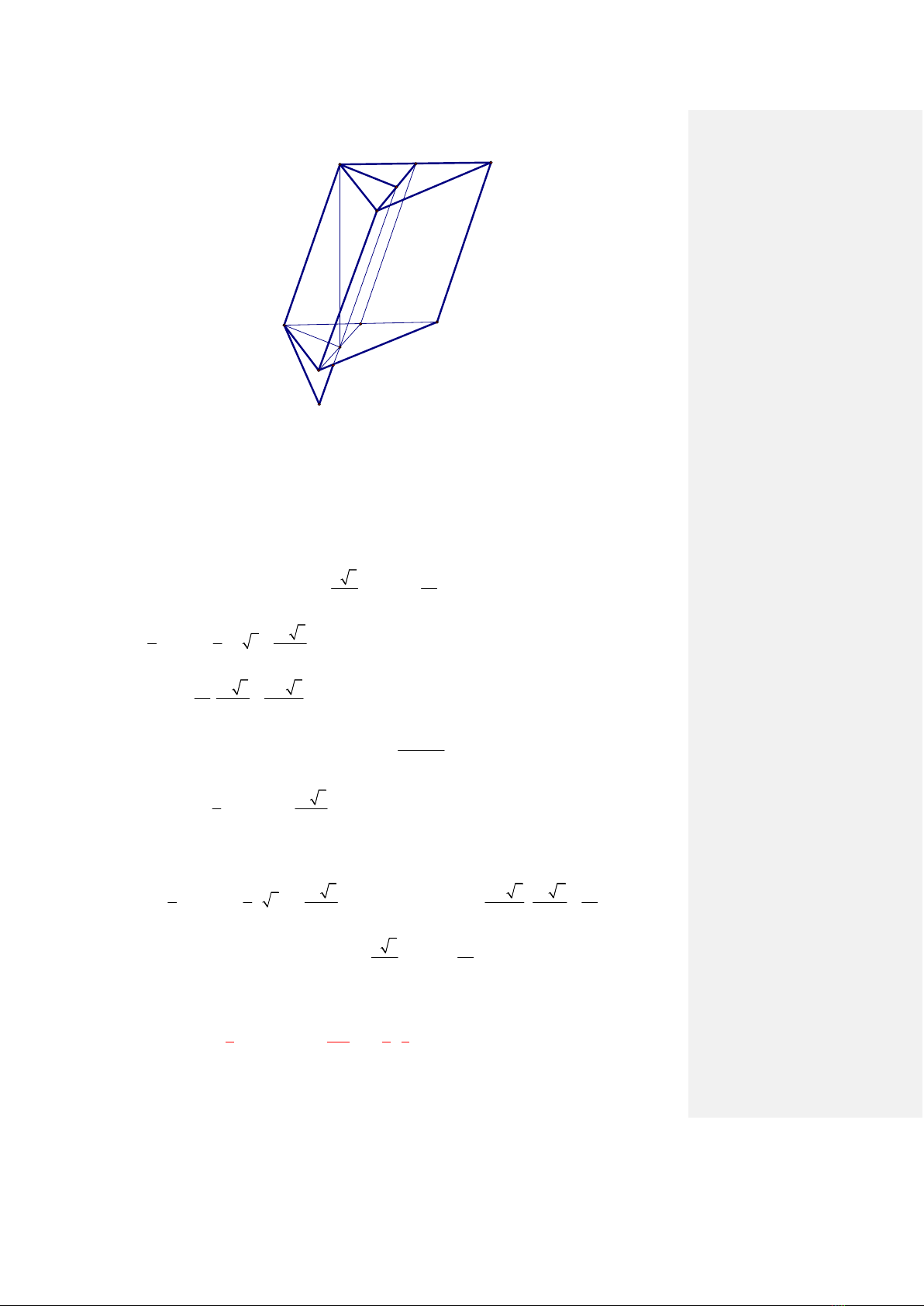
Câu 2. Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, ACB = 300; M là trung điểm cạnh
AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 600. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng
(ABC) là trung điểm H của BM. Tính theo a khoảng cách từ C’ đến mặt phẳng (BMB’).
A.
5.
2
a B.
3.
3
a
C.
3.
4
a
D.
2.
2
a
Lời giải
Chọn C
A
C
B
A'
B'
C'
M
H
Trang 2/28 - Mã đề thi 157
' '
A H ABC A H
là đường cao của hình lăng trụ.
AH là hình chiếu vuông góc của AA’ lên (ABC)
. ’ ’ ’
0
'A 60
' .
ABC A B C
ABC
A H
V A H S
3 3
2 ,MA MB AB a AH '
2 2
a a
AC a A H
2
1 1 3
. . 3
2 2 2
ABC
a
S BA BC a a
2 3
. ' ' '
3 3 3 3
.
2 2 4
ABC A B C
a a a
V
. '
'
3
', ' , ' A, '
A BMB
BMB
V
d C BMB d C BMB d BMB S
3
. ' B'.AMB . ' ' '
1 3
6 8
A BMB ABC A B C
a
V V V
Do
'
BM AHA
nên
' ' ' BM AA BM BB BMB
vuông tại B .
2
'
1 1 3
'. 3.a .
2 2 2
BMB
a
S BB BM a Suy ra
3 2
3 3 2 3
'; ' :
8 2 4
a a a
d C BMB
(Cách 2:
0
3 3
A, ' .sin .sin 60 )
2 4
a a
d BMB AE AH AHE
Vậy chọn đáp án
C.
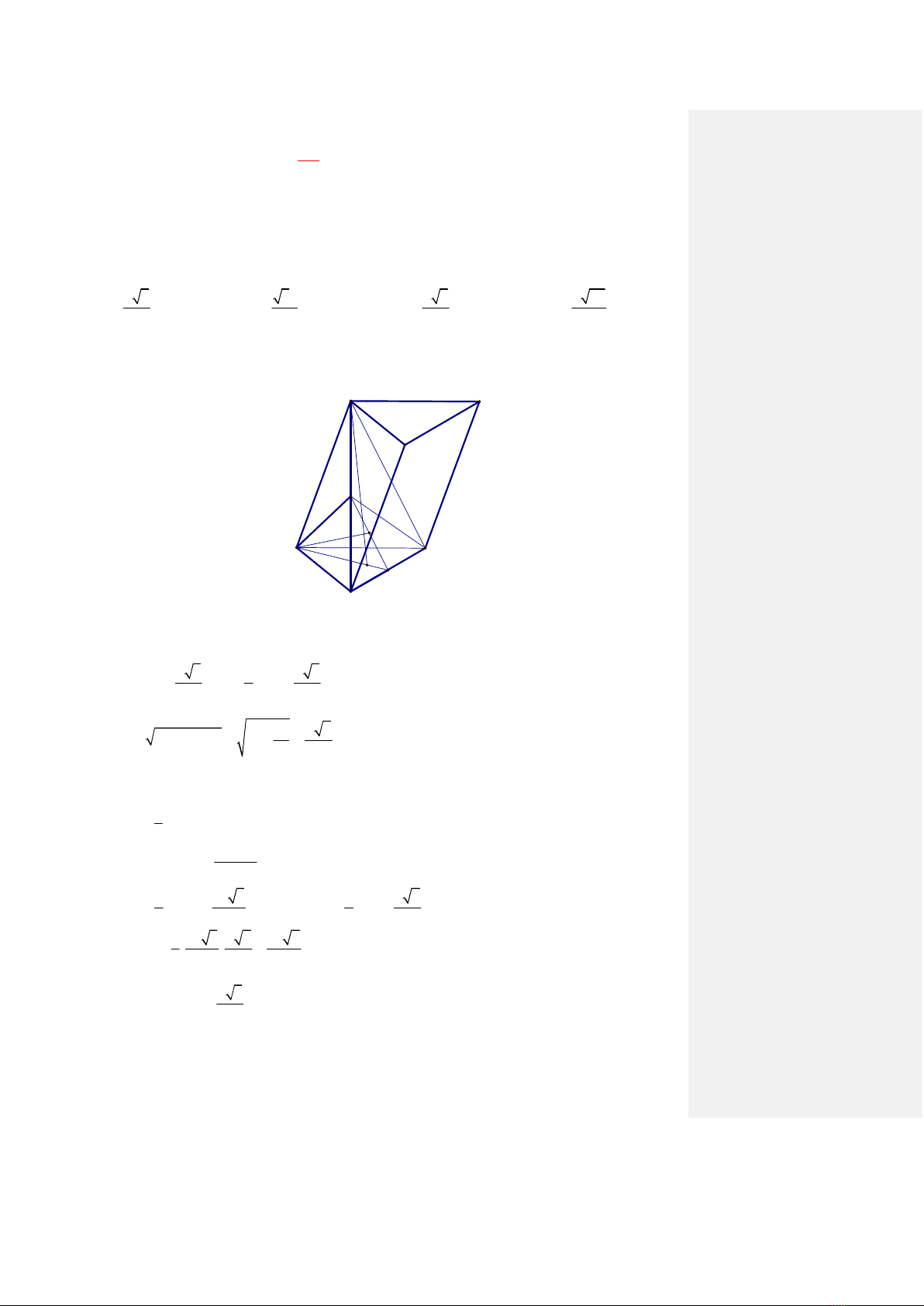
DẠNG 3. KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG
^
P
Q
H
M
A
B
C
C'
B'
A'
E
Trang 3/28 - Mã đề thi 157
KHOẢNG CÁCH TỪ ĐƯỜNG THẲNG ĐẾN MẶT PHẲNG
Cho hình lăng trụ .
ABC A B C
có tất cả các cạnh bên và cạnh đáy đều bằng
a
. Hình chiếu vuông góc của
A
trên mp
A B C
trùng với trung điểm của
B C
.
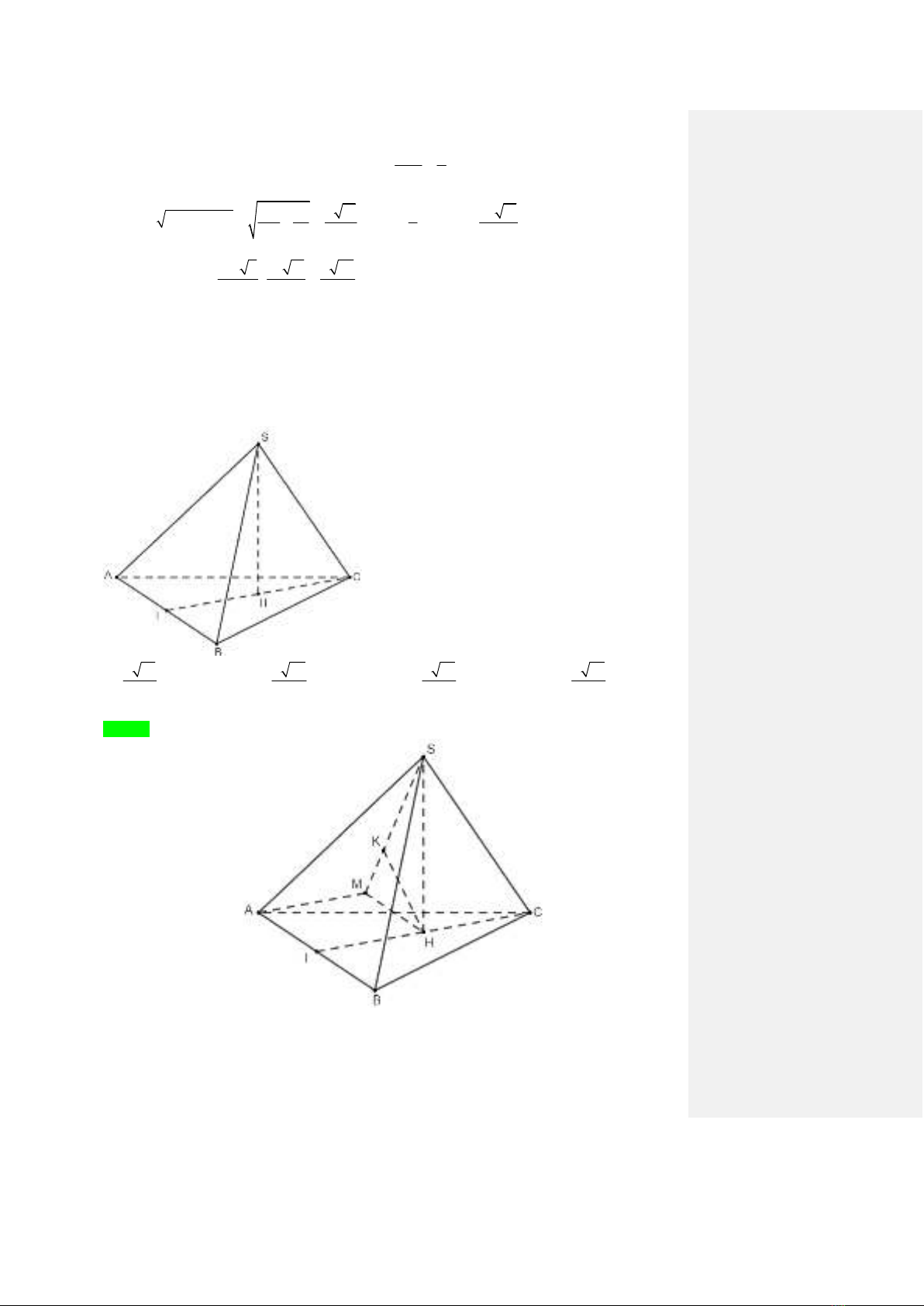
Câu 3. Cho hình lăng trụ ABC. A’B’C’,
ABC
đều có cạnh bằng a, AA’ = a và đỉnh A’ cách đều A, B,C .
Gọi M, N lần lượt là trung điểm của cạnh BC và A’B . Tính theo a khoảng cách từ C đến mặt phẳng
(AMN).
A.
5.
23
a B.
3.
33
a
C.
5.
22
a D.
22 .
11
a
Lời giải
Chọn D
Gọi O là tâm tam giác đều ABC
'
A O ABC
Ta có
3 2 3
,
2 3 3
a a
AM AO AM
2
2 2 2
6
' ' ;
3 3
a a
A O AA AO a
Ta có:
2
2 2
1.d ,
3
3
d ,
1 3 1 6
;d , 'O
2 8 2 6
1 3 6 2
. .
3 8 6 48
NAMC AMC
NAMC
AMC
AMC ABC
NAMC
V S N ABC
V
N ABC S
a a
S S N ABC A
a a a
V
Lại có:
3,
2
a
AM AN nên
AMN
cân tạiA.
N
E
M
A
B
C
C'
B'
A'
O
Trang 4/28 - Mã đề thi 157
Gọi E là trung điểm của MN, suy ra
'
,2 2
A C a
AE MN MN
2 2 2
2 2
3 11 1 11
; .
4 16 4 2 16
AMN
a a a a
AE AN NE S MN AE
2 2
3 2 11 22
; :
48 16 11
a a a
d C AMN
(đvđd)
Vậy chọn đáp án
D.
Câu 4. (SỞ GD-ĐT PHÚ THỌ-Lần 2-2018-BTN) Cho hình chóp .S ABC có đáy là tam giác đều cạnh
bằng
a
. Gọi I là trung điểm
,AB
hình chiếu của S lên mặt phẳng
ABC là trung điểm của
,CI
góc giữa SA và mặt đáy bằng 45 ( tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường
thẳng SA và CI .bằng
A. 14 .
8
a B. 77 .
22
a C. 21 .
7
a D. 21 .
14
a
Lời giải
Chọn B
Do CI AB nên ta dựng hình chữ nhật
AIHM
. Vẽ
HK SM
tại K
Khi đó
HK SAM hay
,HK d H SAM
Trang 5/28 - Mã đề thi 157
Ta có: //
CI AM
nên
//
CI SAM
. Suy ra
, , ,
d CI SA d CI SAM d H SAM HK
AHI
vuông tại
2
2
2 2
3 7
2 4 4
a a a
I AH AI HI
AHS
vuông cân tại
7
4
a
H SH AH
SHM
vuông cân tại 2 2 2 2 2 2
1 1 1 16 4 44 77
7 7 22
a
H HK
HK SH HM a a a
.
Câu 5. Cho hình lăng trụ tứ giác đều
. ' ' ' 'ABCD A B C D
có cạnh đáy bằng
a
. Gọi
, ,M N P
lần lượt là trung
điểm của
, , ' 'AD DC A D
. Tính khoảng cách giữa hai mặt phẳng
( )MNP
và
( ')ACC
.
A.
3
a
. B.
2
4
a. C.
3
3
a. D.
4
a
.
Lời giải
Chọn B
Ta có: Trong tam giác
ACD
:
/ /MN AC
(1)
.
Trong hình vuông
' 'AA D D
:
'
/ / ' '
'
AM A P
AM A P AMPA
AA AM
là hình chữ nhật.
/ / ' / / 'MP AA MP CC
.
Từ
(1)
và
(2)
suy ra:
( ) / /( ')MNP ACC
.
(( ),( ')) ( ,( '))d MNP ACC d I ACC
(với
I
là trung điểm
MN
).
Gọi
O AC BD
.
Mặt khác:
( ')
'
IO AC
IO ACC
IO CC
( ,( '))
d I ACC IO
.
Mà:
1 1 1 2
2
2 4 4 4
a
IO DO BD a .
Suy ra:
2
(( ),( '))
4
a
d MNP ACC .
Câu 6. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D,
3 , .AB a AD DC a
Gọi I là trung
điểm của AD, biết hai mặt phẳng
SBI
và
SCI
cùng vuông góc với đáy và mặt phẳng
SBC
tạo với
đáy một góc
0
60 .
Tính khoảng cách từ trung điểm cạnh SD đến mặt phẳng
.SBC
A.
15 .
20
a B.
6.
19
a C.
3.
15
a D.
a 17 .
5
Hướng dẫn giải
Chọn A
B
A'
D'
C'
B'
A
C
D
M
N
P