ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG NĂM 2010
Môn thi : TOÁN
Thời gian 180 phút (không kể thời gian giao đề)
ĐỀ 14
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
Câu I (2 điểm):
1).Khảo sát và vẽ đồ thị (C) của h.số :
3x 4
y
x 2
. Tìm điểm thuộc (C) cách đều 2 tiệm cận .
2).Tìm các giá trị của m để phương trình sau có 2 nghiệm trên đoạn
2
0;
3
.
sin6x + cos6x = m ( sin4x + cos4x )
Câu II (2 điểm):
1).Tìm các nghiệm trên
0; 2
của phương trình : sin 3x sin x
sin 2x cos2x
1 cos2x
2).Giải phương trình: 3 3
x 34 x 3 1
Câu III (1 điểm): Cho chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = 2, BC = 4. Cạnh bên SA
= 5 vuông góc với đáy. Gọi D là trung điểm cạnh AB.
1).Tính góc giữa AC và SD; 2).Tính khoảng cách giữa BC và SD.
Câu IV (2 điểm): 1).Tính tích phân: I =
2
0
sin x cosx 1
dx
sin x 2cosx 3
2). a.Giải phương trình sau trên tập số phức C : | z | - iz = 1 – 2i
b.Hãy xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thoả mãn
1 < | z – 1 | < 2
PHẦN TỰ CHỌN: Thí sinh chọn câu V.a hoặc câu V.b
Câu V.a.( 2 điểm ) Theo chương trình Chuẩn
1).Viết phương trình các cạnh của tam giác ABC biết B(2; -1), đường cao và đường phân giác trong
qua đỉnh A, C lần lượt là : (d1) : 3x – 4y + 27 = 0 và (d2) : x + 2y – 5 = 0
2). Cho các đường thẳng:
1
x 1
d : y 4 2t
z 3 t
và
2
x 3u
d : y 3 2u
z 2
a. Chứng minh rằng (d1) và (d2) chéo nhau.
b. Viết phương trình mặt cầu (S) có đường kính là đoạn vuông góc chung của (d1) và (d2).
3). Một hộp chứa 30 bi trắng, 7 bi đỏ và 15 bi xanh . Một hộp khác chứa 10 bi trắng, 6 bi đỏ và 9 bi
xanh . Lấy ngẫu nhiên từ mỗi hộp bi một viên bi . Tìm xác suất để 2 bi lấy ra cùng màu .
Câu V.b.( 2 điểm ) Theo chương trình Nâng cao
1).Cho tam giác ABC vuông tại A, p.trình đt BC là :
3
x – y -
3
= 0, các đỉnh A và B thuộc Ox và
bán kính đ.tròn nội tiếp tam giác ABC bằng 2 . Tìm tọa độ trọng tâm G của tam giác ABC.
2).Cho đ.thẳng (d) :
x t
y 1
z t
và 2 mp (P) : x + 2y + 2z + 3 = 0 và (Q) : x + 2y + 2z + 7 = 0
a. Viết phương trình hình chiếu của (d) trên (P)
b. Lập ptr mặt cầu có tâm I thuộc đường thẳng (d) và tiếp xúc với hai mặt phẳng (P) và (Q)
3). Chọn ngẫu nhiên 5 con bài trong bộ tú lơ khơ . Tính xác suất sao cho trong 5 quân bài đó có đúng
3quân bài thuộc 1 bộ ( ví dụ 3 con K )
HƯỚNG DẪN GIẢI: (đề số 14)
C©u Néi dung §iÓm
Gäi M(x;y)
(C) vµ c¸ch ®Òu 2 tiÖm cËn x = 2 vµ y = 3
| x – 2 | = | y – 3 |
3x 4 x
x 2 2 x 2
x 2 x 2
x 1
xx 2
x 4
x 2
VËy cã 2 ®iÓm tho¶ m·n ®Ò bµi lµ : M1( 1; 1) vµ M2(4; 6)
2
0.75
®
XÐt ph¬ng tr×nh : sin6x + cos6x = m ( sin4x + cos4x ) (2)
2 2
3 1
1 sin 2x m 1 sin 2x
4 2
(1)
§Æt t = sin22x . Víi
2
x 0;
3
th×
t 0;1
. Khi ®ã (1) trë thµnh :
2m =
3t 4
t 2
víi
t 0;1
NhËn xÐt : víi mçi
t 0;1
ta cã : sin 2x t
sin 2x t
sin 2x t
0,25
§Ó (2) cã 2 nghiÖm thuéc ®o¹n
2
0;
3
th×
3 3
t ;1 t ;1
2 4
Da vµo ®å thÞ (C) ta cã : y(1)< 2m ≤ y(3/4)
7
1 2m
5
VËy c¸c gi¸ trÞ cÇn t×m cña m lµ :
1 7
;
2 10
0,5
II
2,0® 1
1,0®
sin 3x sin x
sin 2x cos2x
1 cos2x
(1) 2cos2x.sin x 2cos 2x
4
2 sin x
§K : sinx ≠ 0 x
k
Khi
x 0;
th× sinx > 0 nªn :
(1)
2
cos2x =
2
cos 2x
4
x
16 2
k
Do
x 0;
nªn
9
x hay x
16 16
Khi
x ; 2
th× sinx < 0 nªn :
(1)
2
cos2x =
2
cos 2x
4
cos -2x = cos 2x-
4
5
x
16 2
k
0,5
Do
x ; 2
nªn
21 29
x hay x
16 16
0,5
2
1,0®
§Æt 3 3
u x 34, v x 3
. Ta cã :
2 2
3 3
u v 1
u v 1
u v u v uv 37
u v 37
2
u v 1
u v 1
uv 12
u v 3uv 37
u 3
v 4
u 4
v 3
Víi u = -3 , v = - 4 ta cã : x = - 61
Víi u = 4, v = 3 ta cã : x = 30
VËy Pt ®· cho cã 2 nghiÖm : x = -61 vµ x = 30
0,25
0,5
0.25
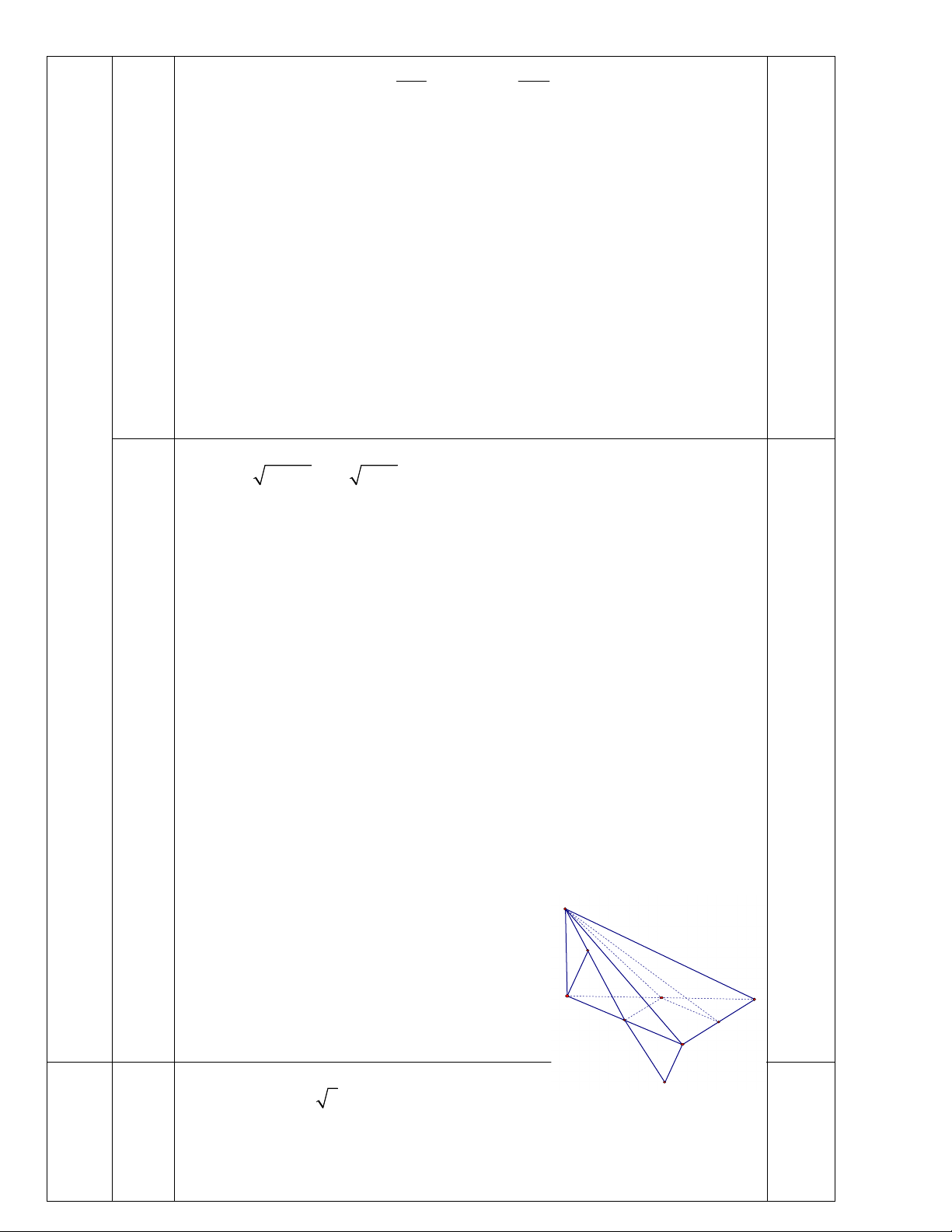
III
1.0®
1®
a)Ta cã : AB =
2 5
,
Gäi M lµ trung ®iÓm cña BC ,
NM
D
S
AB
C
K