TRƯ
ỜNG PTTH CHUY
ÊN LÊ QUÝ
ĐÔN Đ
Ề THI THỬ ĐẠI HỌC
L
ẦN II
TỈNH QUẢNG TRỊ Môn: Toán; khối A+A1
Thời gian làm bài: 180 phút, không kể thời gian phát đề
I.PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm):
Câu 1(2 điểm).Cho hàm số:
2
2
x
y
x
=
−
a)Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
b)Viết phương trình tiếp tuyến với đồ thị (C ) biết tiếp tuyến cắt các trục Ox, Oy lần lượt tại A, B sao
cho tam giác OAB thỏa mãn:
2
ABOA
=( O là gốc tọa độ)
Câu 2(1điểm). Giải phương trình:
(
)
23cot1 15
3cot42os1
sinx4
x
xcx π
+

+−+=


Câu 3(1điểm). Giải hệ phương trình:
22
22
217
12
xyxy
yxy
++−=
−=
Câu 4(1điểm). Tính tích phân:
(
)
( )
2
1
12ln1
1
exx
Idx
xx
+−
=+
∫
Câu 5(1điểm). Cho hình chóp SABCD có SA vuông góc với đáy, đáy ABCD là nửa lục giác đều nội
tiếp trong đường tròn đường kính AD, với AD = 2a. Gọi I là trung điểm của AB, biết khoảng cách từ I
tới mặt phẳng (SCD) bằng
33
8
a
. Tính thể tích khối chóp SABCD theo a và cosin của góc tạo bởi hai
đường thẳng SO và AD, với O là giao điểm của AC và BD.
Câu 6(1điểm). Cho các số thực dương x, y thỏa mãn: x + y + 1 = 3xy
Tìm giá trị lớn nhất của biểu thức:
( ) ( )
22
3311
11
xy
P
yxxyxy
=+−−
++
II. PHẦN RIÊNG: Thí sinh chỉ được làm một trong hai phần (phần A hoặc B)
A.Theo chương trình chuẩn:
Câu 7.a (1điểm).Trong mặt phẳng tọa độ Oxy cho hình thoi ABCD có AC = 2 BD và I(2;1) là giao
điểm hai đường chéo. Biết
1
(0;)
3
Mnằm trên đường thẳng AB, N(0;7) nằm trên đường thẳng CD. Tìm
tọa độ điểm B biết B có hoành độ dương.
Câu 8.a(1điểm). Lập phương trình mặt cầu qua A(0;1;3), có tâm I thuộc đường
thẳng
()
12
:
121
xyz
d
+−
==
−và tiếp xúc với mặt phẳng (P):
23620
xyz
+−−=
.
Câu 9.a(1điểm)Cho
0
x
>
và
12322136
2121212121
...2
nnnnn
nnnnn
CCCCC
++++
+++++
+++++=
.Tìm số hạng không chứa x
trong khai triển nhị thức Niu-tơn của 512
n
x
x

−


.
B. Theo chương trình nâng cao
Câu 7.b(1 điểm). Trong mặt phẳng tọa độ Oxy cho đường tròn (C): 22
16
xy
+=
.Viết phương trình
chính tắc của Elip biết tâm sai
1
2
e
=
, Elip cắt đường tròn (C) tại bốn điểm phân biệt A,B,C,D sao cho
AB song song với trục hoành và AB = 2 BC
Câu 8.b(1 điểm). Cho A(3;5;4), B(3;1;4). Tìm điểm C trên mặt phẳng (P):
10
xyz
−−−−
sao cho
tam giác ABC cân ở C và có diện tích bằng
217
.
Câu 9.b(1 điểm). Từ một bộ bài Tú lơ khơ gồm 52 con (13 bộ tứ). Người ta rút 5 con bất kỳ. Tính
xác suất để rút được 2 con thuộc một bộ tứ, 2 con thuộc bộ tứ khác, con thứ 5 thuộc bộ tứ khác nữa.
………………Hết…………………
Thí sinh không được sử dụng tài liệu.Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh………………………………………….Số báo danh……………………….
www.MATHVN.com
www.DeThiThuDaiHoc.com
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC ĐỢT II, MÔN TOÁN,KHỐI A,A1
Câu Nội dung Điểm
I
a)
1đ
Khảo sát sự biến thiên và vẽ đồ thị của hàm số 1đ
TXĐ:
{
}
\2
R
( )
2
4
'0;2
2
yx
x
−
=<∀≠
−
0.25
Hàm số nghịch biến trên mỗi khoảng
(
)
(
)
;2;2;
−∞+∞
Hàm số không đạt cực trị
limlim2
xx
yy
→−∞ →+∞
==⇒
Đồ thị hàm số có tiệm cận ngang y=2
22
lim;lim
xx
yy
−+
→→
=−∞=+∞⇒
Đồ thị hàm số có tiệm cận đứng x =2
0.25
BBT 0.25
Đồ thị: 0,25
b)
1đ Gọi
( )
2
;2
o
o
o
x
MxC
x

∈

−

, (d) là tiếp tuyến của (C) tại M, cắt Ox tại A, Oy
tại B sao cho: 2
ABOAABO
=⇒∆ vuông cân ở O nên hệ số góc của tiếp
tuyến
1
k
=±
0.25
0
0
'()1
4
o
o
x
yx x
=
=−⇔
=
0.25
0():
o
xdyx
=⇒=−
4():8
o
xdyx
=⇒=−+
.Vậy có một tiếp tuyến cần tìm là y = -x + 8
0.25
Tiếp tuyến thỏa mãn bài toán là y= -x+8
Chú ý: Nếu tìm ra mà không loại trường hợp y = -x thì trừ 0.25đ
0.25
2
1đ
Đk; ,
xkkZ
π
≠∈
Pt
( )
2
22
oscossinx
334sinxcos1
sinsin
cxx x
xx
+
⇔+−+=
0.25
(
)
2
(34sin)cossinx10
xx
⇔−++=
0.25
21
34sin0os2 2
1
cossinx1os 4
2
xcx
xcx
π
−
−=⇔=
⇔
−

+=−⇔−=


0.25
3
()
2,2
2
xk
kZ
xkxk
π
π
π
πππ
=±+
⇔∈
−
=+=+
Đối chiếu ĐK ta có nghiệm pt là
3
xk
π
π
=±+ ;
2
2
xk
π
π
−
=+
0.25
3
1đ ĐK: 22
0
xy
−≥
.Đặt
22
tyxy
=+−, hệ trở thành: 22
217
24
xt
xt
+=
−=−
0.25
Giải hệ ta có:
( ) ( )
5355
;5;7;;
33
xt


=−




. 0.25
Từ pt thứ 2 của hệ suy ra y>0 nên t>0. Vậy x=5
4
y
⇒=
hoặc
3
y
=
0.25
Vậy: Nghiệm của hệ là:
(
)
(
)
(
)
{
}
;5;4;5;3
xy =
0.25
www.MATHVN.com
www.DeThiThuDaiHoc.com
Nội dung Điểm
4
1đ I
( ) ( ) ( )
22
111
22ln
1
11
eee
dxxdx
xx xx
=−+
+
++
∫∫∫
0.25
( ) ( )
11
2
111
2112
|
111
1
eee
e
dx
Idxdx
xxxxx
x

=−=−+

+++
+
∫∫∫
1
222
(lnln(1))|ln
111
e
xx
xee
=−++=+
+++
0.25
( )
21
11
112
2ln2ln|
111
ee
e
Ixdxdx
xxxx
−−

==+

+++

∫∫
11
122
2ln|2ln|2ln
1111
ee
xe
x
xxee
−−

=+=+

++++

0.25
Vậy
2
23ln
1
I
e
=+
+
0.25
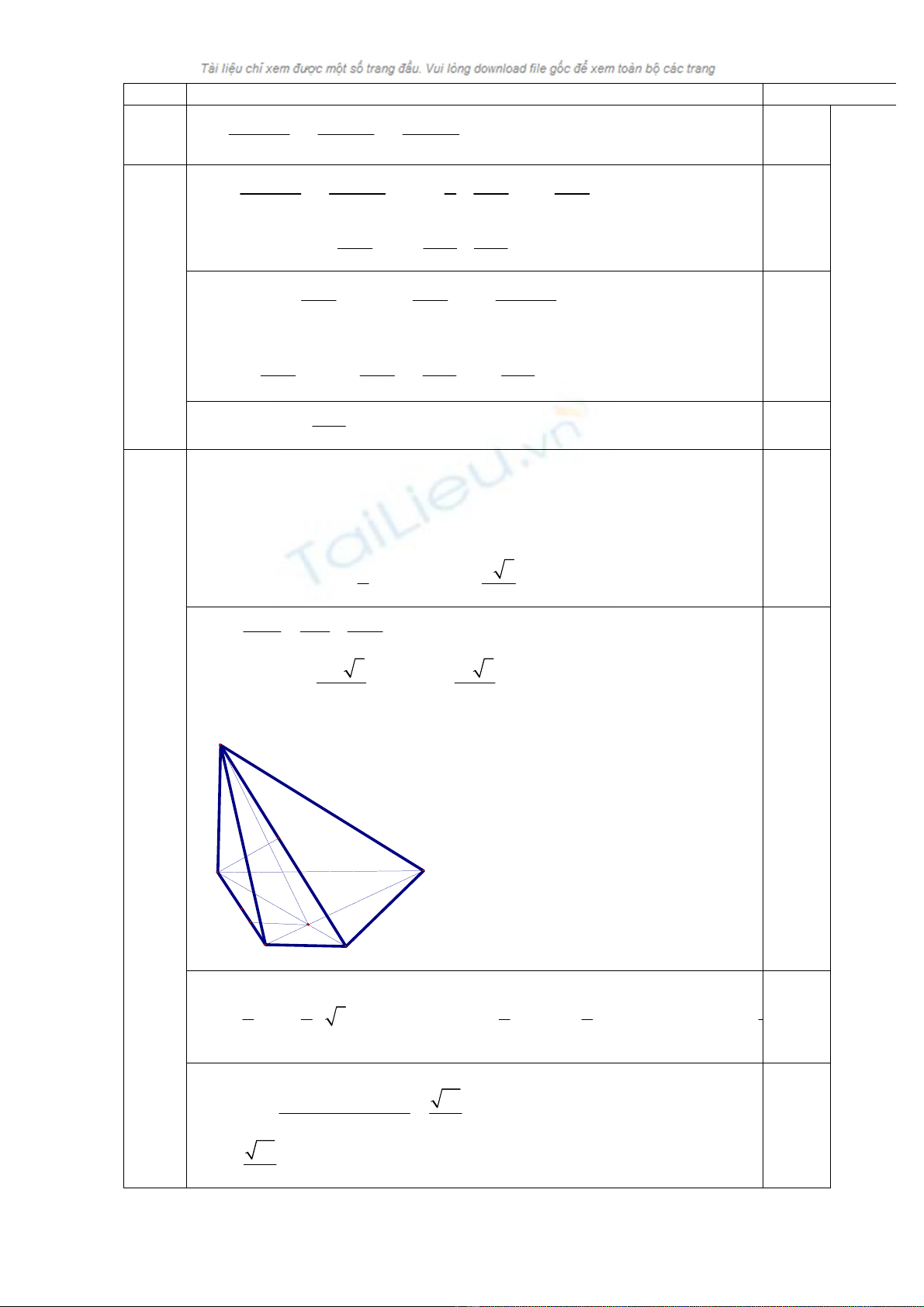
5
1đ
Gọi E là giao điểm của AB và CD, M là trung điểm của AD.
Ta có MA=MC=MD
⇒
ACD vuông ở C
( )
CDCA
CDSAC
CDSA
⊥
⇒⇒⊥
⊥
Kẻ đường cao AH của tam giác SAC thì
(
)
AHSCD
⊥ và
( )
( )
( )
( )
43
,,
32
a
AHdASCDdISCD===
0.25
Ta có: 222
111
SAa
AHSAAC
=+⇔=
23
333
3
44
ABCDMABSABCD
aa
SSV==⇒=
IO
A
D
BC
S
N
H
0.25
Kẻ ON//AD, ta có:
2222222
227213
3,,,
33339
AOACaSOSAAOaONaSNSAAN
===+===+=
0.25
Theo định lý cosin trong tam giác SON,
222
OS21
cos
2.OS7
ONSN
SON
ON
+−
==
. Vậy góc giữa SO và AD bằng
arccos
21
7
0.25
www.MATHVN.com
www.DeThiThuDaiHoc.com