TR◊ÕNG THPT CHUYÊN QUANG TRUNG
TTOÁN
(∑ thi có 6 trang)
ó THI TH€ ÑI H≈C NãM 2020 - 2021
MÔN: TOÁN, LŒP 12, LÜN 1
ThÌi gian làm bài: 90 phút
Mã ∑ thi 111
Câu 1. Trong không gian Oxyz,i∫mA(1; 2; 3)thuÎc ph˜Ïng trình m∞t phØng nào d˜Óiây?
Ax2y+z=0. B x2y+3z=0. C x+2y+3z=1. D x+2y+3z=0.
Câu 2. §o hàm cıa hàm sËy=2021xlà
Ay0=2021x·ln 2021. B y0=2021x
ln 2021·Cy0=2021x. D y0=x·2021x1.
Câu 3. Cho hai hàm sËf(x),g(x)liên tˆc trên R. Trong các mªnh ∑ sau, mªnh ∑ nào sai?
AZf0(x)dx=f(x)+CvÓi mÂi hàm f(x)có §o hàm trên R.
BZkf (x)dx=kZf(x)dxvÓi mÂi h¨ng sËk2R.
CZ⇥f(x)+g(x)⇤dx=Zf(x)dx+Zg(x)dx.
DZ⇥f(x)g(x)⇤dx=Zf(x)dxZg(x)dx.
Câu 4. Cho ba sËd˜Ïng a,b,c(a,1,b,1) và sËth¸cαkhác 0.Øng th˘c nào sai?
Alogabα=1
α
logab.Blogbc=logac
logab·
Clogac=logab.logbc. D loga(b.c)=logab+logac.
Câu 5. Cho hàm sËy=f(x)có b£ng bi∏n thiên nh˜sau
x
y0
y
1 13+1
+00+
11
44
22
+1+1
Hàm sË Áng bi∏n trên kho£ng nào sau ây?
A(1; 3). B (1;4
). C (0; +1). D (3; +1).
Câu 6. Có bao nhiêu lo§i khËia diªn∑u?
A3. B 6. C 5. D 4.
Câu 7. Trong không gian Oxyz, tìm tÂaÎ hình chi∏u cıaM(1; 2; 3)lên m∞t phØng Oxz.
A(1; 0; 3). B (0; 2; 0). C (1; 2; 3). D (1; 2; 3).
Câu 8.
Cho hàm sËy=f(x)có Á th‡nh˜hình v≥. Mªnh ∑ nào d˜Óiây úng?
A Hàm sË §t c¸c§i t§ix=1.
B Hàm sË §t c¸c ti∫u t§ix=0.
C Hàm sË §t c¸c§i t§ix=0.
D Hàm sË §t c¸c§i t§ix=1và x=1.
x
y
0
1 1
1
Trang 1/6 Mã ∑ 111
HÂvà tên hÂc sinh:..............................................
LÓp: ...........................................................
Câu 9. Trong không gian Oxyz, gÂiAlà i∫m thuÎc m∞t cu tâm Ibán kính R. KhØng ‡nh nào sau ây là
úng?
AIA =R2. B IA =R. C IA <R. D IA >R.
Câu 10. Cho hàm sËf(x)liên tˆc trên [a,b]. GÂiF(x)là mÎt nguyên hàm cıa hàm sËf(x). KhØng ‡nh nào
sau ây là úng?
A
b
Z
a
f(x)dx =F(b)+F(a).B
b
Z
a
f(x)dx =F2(b)F2(a).
C
b
Z
a
f(x)dx =F(a)F(b).D
b
Z
a
f(x)dx =F(b)F(a).
Câu 11. Cho sËph˘cz=a+bi (a,b2R). KhØng ‡nh nào sau ây là úng?
A Phn£o cıa sËph˘czlà bi. B Phn£o cıa sËph˘czlà b.
C Phn th¸c cıa sËph˘czlà b. D Mô un cıa sËph˘czlà a2+b2.
Câu 12. Trong không gian Oxyz,˜Ìng thØng Ox có ph˜Ïng trình nào d˜Óiây?
A8
>
>
>
>
<
>
>
>
>
:
x=1
y=t
z=t.
B8
>
>
>
>
<
>
>
>
>
:
x=1
y=0
z=0.
C8
>
>
>
>
<
>
>
>
>
:
x=t
y=0
z=0.
D8
>
>
>
>
<
>
>
>
>
:
x=t
y=1
z=1.
Câu 13.
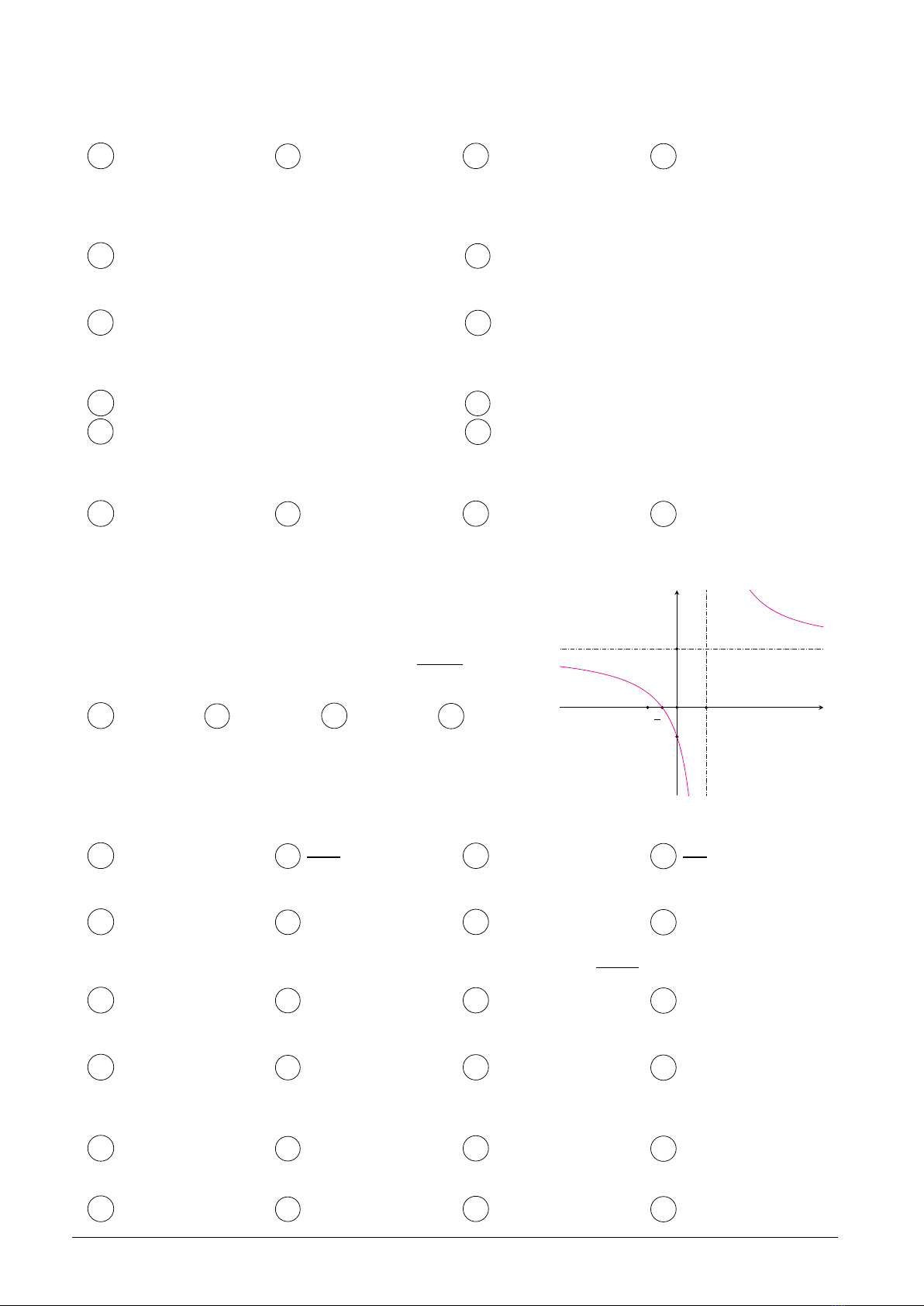
˜Ìng cong hình bên là Á th‡cıa hàm sËy=ax +b
cx +dvÓia,b,c,d
là các sËth¸c. Giá tr‡nh‰nhßt cıa hàm sËtrên [1; 0]là
A0. B 1.C1. D 2.0
1
21
2
1
1x
y
Câu 14. KhËi trˆcó bán kính áy, ˜Ìng cao ln l˜Òt là a,2athì có th∫tích b¨ng
A2πa3. B 2πa3
3·Cπa3. D πa3
3·
Câu 15. Nguyên hàm cıa hàm sËf(x)=2x(x1)(2x1) là
Ax4x3+x2+C.Bx4+x32x2+C. C x4+x3+x2+C. D ⇣x2x⌘2
+C.
Câu 16. TÍng sËtiªm c™n˘ng và tiªm c™n ngang cıaÁ th‡hàm sËy=x+1
x21là
A3. B 2. C 4. D 1.
Câu 17. T™p xác ‡nh Dcıa hàm sËy=log2021(x1)2+log2020 ⇣4x2⌘là
AD=(1; 2). B D=(2; 2)\{1}. C D=(2; 1). D D=[2; 2].
Câu 18. GÂiz1,z2là nghiªm cıa ph˜Ïng trình z22z+2=0, bi∏t sËph˘cz1có phn£o âm. Phn£o cıa sË
ph˘cz2là
Ai. B 1. C 1i. D 1.
Câu 19. TÍng giá tr‡lÓn nhßt và nh‰nhßt cıa hàm sËy=x33xtrên [1; 2]b¨ng
A3.B2. C 1. D 0.
Trang 2/6 Mã ∑ 111
Câu 20. SËgiao i∫m cıaÁ th‡hàm sËy=x3+x22x+2và Á th‡hàm sËy=x22x+3là
A3. B 1. C 2. D 0.
Câu 21. Trong không gian Oxyz, bi∏t ph˜Ïng trình m∞t cu(S): x2+y2+z2=25 c≠t m∞t phØng (P): x+y+z=
3theo giao tuy∏n là mÎt˜Ìng tròn có bán kính r. Khi ó giá tr‡cıarlà
A3.B5. C 4. D 5
3.
Câu 22. Cho z2Cth‰az+2|z|=12. Phn£o cıa sËph˘czlà
A2. B 0. C 12. D 4.
Câu 23. T™p nghiªm cıa bßt ph˜Ïng trình log2x+log2(x+1)1là
A(0; 1]. B [1; +1). C (2; 1]. D (1;2][[1; +1).
Câu 24. Cho F(x)là nguyên hàm cıa hàm sËf(x)=x.ex, bi∏tF(1) =0. Hàm F(x)là
Ax.exex. B x.ex+ex1. C x.exe. D x.exx+1e.
Câu 25. Cho hình chóp ∑uS.ABCD có áy là hình vuông c§nh a, c§nh bên SA =2a. Th∫tích cıa khËi
chóp S.ABCD là
Aa3.r7
2.Bp14
6a3·C2a3. D p14a3
2·
Câu 26. TÍng tßt c£các nghiªm cıa ph˜Ïng trình 2x2+2x=8b¨ng
A2. B 3. C 2. D 1.
Câu 27. Hình nón có bán kính áy, ˜Ìng cao ln l˜Òt là 3,4. Diªn tích xung quanh hình nón b¨ng
A15π
2·B15π. C 12π. D 6π.
Câu 28. Cho hình l™p ph˜Ïng ABCD.A0B0C0D0có c§nh b¨ng a. Th∫tích khËi t˘diªnABDB0là
Aa3
2·Ba3
3·C2a3
3·Da3
6·
Câu 29. Cho hình l´ng trˆA1A2A3A4A5.B1B2B3B4B5. SË o§n thØng có hai ønh là ønh hình l´ng trˆlà
A60. B 45. C 35. D 90.
Câu 30. Trong không gian Oxyz, tìm ph˜Ïng trình m∞t phØng c≠t tia Ox,Oy,Oz t§iA,B,Cvà nh™nG(673; 674; 675)
làm trÂng tâm cıa tam giác ABC.
Ax
673 +y
674 +z
675 =0.Bx
673 +y
674 +z
675 =1.
Cx
2019 +y
2022 +z
2025 =0.Dx
2019 +y
2022 +z
2025 =1.
Câu 31. KhØng ‡nh nào úng v∑tính Ïniªu cıa hàm sËy=x+2
x1?
A Hàm sË Áng bi∏n trên các kho£ng (1;1
)và (1; +1).
B Hàm sË Áng bi∏n trên các kho£ng (1;1
)[(1; +1).
C Hàm sËngh‡ch bi∏n trên các kho£ng (1;1)và (1; +1).
D Hàm sËngh‡ch bi∏n trên các kho£ng (1;1
)và (1; +1).
Câu 32. Cho hàm sËy=x42x2+2021.i∫m c¸c§i cıa hàm sËlà
A(0; 2021). B x=0. C x=1. D x=1.
Câu 33. Trong không gian Oxyz, tìm tÂaÎ i∫mËi x˘ng vÓiM(0; 1; 2) qua m∞t phØng x+y+z=0.
A(2; 1; 0). B (0; 1; 2). C (0; 1; 2). D (4; 2; 0).
Câu 34. Cho ph˜Ïng trình log2
2xlog2
x3
4!pexm=0. GÂiSlà t™p hÒp giá tr‡mnguyên vÓim2
[10 ; 10]∫ ph˜Ïng trình có úng 2nghiªm. TÍng giá tr‡các phn t˚cıaSb¨ng
A28.B12. C 3. D 9.
Trang 3/6 Mã ∑ 111
Câu 35. Trong không gian Oxyz, cho hai i∫mA(3; 2; 3); B(1; 0; 5). Tìm tÂaÎ i∫mM2(Oxy)sao cho
MA +MB §t giá tr‡nh‰nhßt.
A 9
4;5
4;0
!.B 9
4;5
4;0
!.C 9
4;5
4;0
!.D 9
4;5
4;0
!.
Câu 36. ∫ l≠p∞t hªthËng iªn n´ng l˜Òng m∞t trÌi 50KWP, gia ình b§n A vay ngân hàng sËti∑n là 600
triªuÁng vÓi lãi sußt0,6%/tháng. Sau úng mÎt tháng k∫t¯ngày l≠p∞t, gia ình b§n A b≠t¶u˜a vào
v™n hành hòa l˜Ói thì mÈi tháng công ty iªn l¸c tr£gia ình b§n A 16 triªuÁng. Nên sau úng 1 tháng k∫
t¯ngày vay, gia ình b§n A b≠t¶u hoàn nÒ, hai ln hoàn nÒcách nhau úng mÎt tháng, mÈi tháng hoàn nÒ
sËti∑n là 16 triªuÁng. H‰i sau bao nhiêu tháng, gia ình b§n A s≥tr£h∏t nÒ?
A44. B 45. C 42. D 43.
Câu 37. F(x)là mÎt nguyên hàm cıa hàm f(x)=(x1)px22x3. Bi∏tF(2)=F(4)1=5p5
3và
F(3)+F(5)=ap3+b;a,b2N. Giá tr‡a+bb¨ng
A9. B 17. C 12. D 18.
Câu 38. Cho sËph˘czth‰a mãn (|z12i|1
|z24i|2.Giá tr‡S=min |z|+max |z|b¨ng
Ap5+2. B p2+p51. C 2p5+1. D 3p51.
Câu 39. Cho hàm sËy=f(x)có b£ng bi∏n thiên nh˜sau
x
y0
y
1 101+1
0+00+
+1+1
22
33
11
+1+1
Ph˜Ïng trình 2f sin x+cos x
p2!+3=0có bao nhiêu nghiªm trên "3π
4;7π
4#?
A5. B 6. C 4. D 3.
Câu 40. Cho hàm sËy=f(x)có b£ng bi∏n thiên nh˜sau
x
y0
y
1 101+1
+00+0
11
22
33
22
11
Hàm sËy=f(12x)+1Áng bi∏n trên
A 0; 3
2!.B 1
2;1
!.C(1; +1). D 1; 1
2!.
Câu 41. Cho
π
4
Z
0
xdx
1sin2x
=
π
aln b+ln p2; a,b2N⇤. Giá tr‡a+3bb¨ng
A8.B10. C 12. D 4.
Trang 4/6 Mã ∑ 111
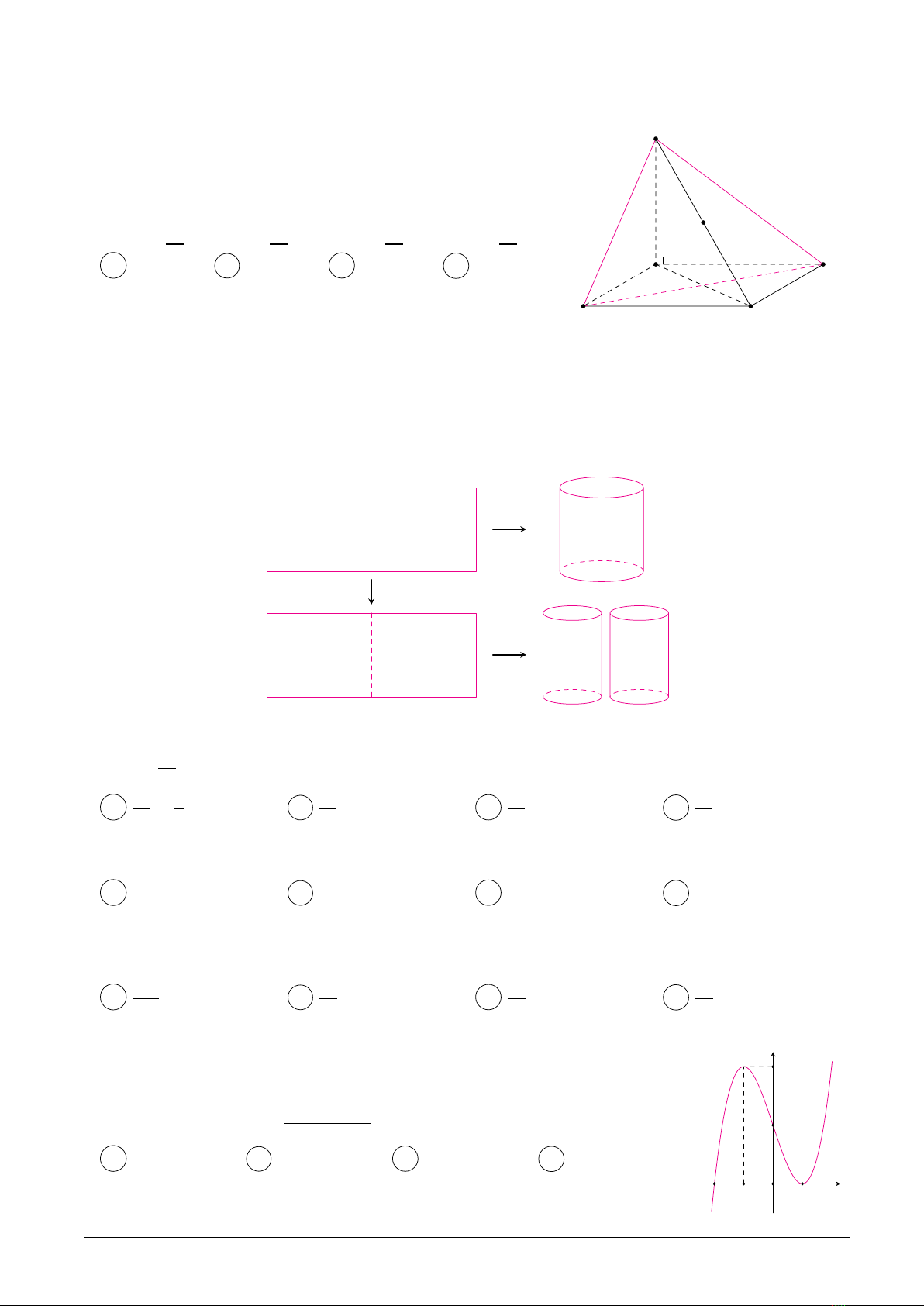
Câu 42.
Cho hình chóp S.ABCD áy là hình thoi c§nh a,∠BAD =60,
SA vuông góc vÓi m∞t phØng (ABCD). Góc gi˙a˜Ìng thØng SC
và m∞t phØng (ABCD)b¨ng 45. GÂiIlà trung i∫mSC. Kho£ng
cách t¯I∏n m∞t phØng (SBD
)là
A2ap15
5·Bap15
10 ·Cap15
5·Dap15
15 ·
B
A
C
D
S
I
Câu 43. T¯mÎt tßm tôn hình ch˙nh™t kích th˜Óchvà a, ng˜Ìi ta làm các thùng ¸ng n˜Óc hình trˆcó chi∑u
cao b¨ng h, theo hai cách sau (xem hình minh hÂa d˜Óiây):
•Gò tßm tôn ban ¶u thành m∞t xung quanh cıa thùng.
•C≠t tßm tôn ban ¶u thành hai tßm b¨ng nhau, rÁi gò mÈi tßmó thành m∞t xung quanh cıa mÎt thùng.
Kí hiªuV1là th∫tích cıa thùng gò ˜Òc theo cách 1 và V2là tÍng th∫tích cıa hai thùng gò ˜Òc theo cách 2.
Tính tøsËV1
V2
·
AV1
V2
=1
2·BV1
V2
=1.CV1
V2
=2.DV1
V2
=4·
Câu 44. GÂiSt™p hÒp các giá tr‡m∫ Á th‡hàm sËy=x42m2x2+1có 3i∫m c¸c tr‡t§o thành mÎt tam
giác vuông cân. TÍng bình ph˜Ïng các phn t˚cıa t™pSb¨ng
A4. B 2. C 6. D 8.
Câu 45. Có 6hÂc sinh gÁm2hÂc sinh tr˜Ìng A,2hÂc sinh tr˜Ìng Bvà 2hÂc sinh tr˜Ìng Cs≠p x∏p trên
mÎt hàng dÂc. Xác sußt∫ ˜Òc cách cách s≠p x∏p mà hai hÂc sinh tr˜Ìng Cthì mÎt em ngÁi gi˙a hai hÂc
sinh tr˜Ìng Avà mÎt em ngÁi gi˙a hai hÂc sinh tr˜Ìng Blà
A1
180·B1
30·C1
90·D1
45·
Câu 46.
Cho hàm sËy=f(x)=ax3+bx2+cx +d, có Á th‡nh˜hình v≥. SË ˜Ìng tiªm c™n
˘ng cıaÁ th‡hàm sËy=x2+x2
f2(x)f(x)là
A3. B 2. C 4. D 5.
0
211
2
4
x
y
Trang 5/6 Mã ∑ 111