Phn chung cho tt c thí sinh (7 im):
Câu I(2.
) :
1.Kho sát s bin thiên và v th (C) :
3
32
yxx
=−+
.
2.Vit phng trình ng thng ct th (C) ti 3 im phân bit A;B;C sao cho x
A
= 2
và BC=
22
Câu II (2.
):
Gii bt phng trình
)
3
(log
5
3
log
log
2
4
2
2
2
2
−
>
−
−x
x
x
Tìm
)
;
0
(
π
∈
x
tho mãn
phng trình
cotx-1=
x
x
x
x2
sin
2
1
sin
tan
1
2
cos
2
−
+
+
Câu II (1.
)
: Tính các tích phân sau :
=+
2
I
=
1
2
0
ln(1)
(2)
xdx
x
+
+
Câu IV (1.
)
:

  

   
2
⊥
!
"#$
%&
'
(
)*
+
,-
. /&
0
-
. /%
1-
+
2- !
"
⊥
!
%"34
.
4
56
17
8
A
NIB
Câu V
(1.
): Cho 3 s
d
ng x,y,z tho
mãn : x+ y +z = 1. Tìm giá tr
l
n nh
t c
a bi
u th
c :
xyyzzx
Pxy z yz x zx y
=++
+ + +
.
Phn riêng (3 im)
Thí sinh ch c làm mt trong hai phn (phn A hoc phn B)
A.Theo ch
ng trình Chun:
Câu VI A.(2.
)
: 1.
Trong mt phng ta Oxy cho im A(3; 2) , các ng thng
∆
1
: x + y – 3 = 0 và ng thng ∆
2
: x + y – 9 = 0. Tìm ta im B thuc ∆
1
và im C thuc
∆
2
sao cho tam giác ABC vuông cân ti A.
∆ !
=
−
="
#
$
%
α
&'
&(
)
*
+
,
%
-
#
.
,
/
0
1
/
2
3
43
5
#
α "
6
%
"
7
∆ #
8
7
9(
CâuVIIA(1)
Cho khai trin (1 + x + x
2
+ x
3
)
5
= a
0
+ a
1
x + a
2
x
2
+ a
3
x
3
+ …+ a
15
x
15
. Tìm h s a
10.
B.Theo ch
ng trình Nâng cao:
Câu VI.B(2.
)

)9-
+
:!
");-
+
22
4440
xyxy
+−−+=)9-
<-!
7"
);-+=>?@ 1- +2-!7",AB! "C. DE8 &3 C
F
.
+
G)9-
+
:!
"H7
8
4
-
I
2.Trong không gian 0xyz cho 2 ng thng : (
∆
1
):
−
=
=
+
=
t
z
ty
t
x
2
1
t∈
R và (
∆
2
)
−
=
+=
=
'
'1
0
t
z
ty
x
't∈
R
Chng minh rng
∆
1
và
∆
2
chéo nhau .Vit phng trình ng vuông góc chung ca 2 ng
thng
∆
1
và
∆
2
CâuVII.B(1.
) :
Cho khai trin
()
x1
3x12
2
8
1log31
log975
2 2
−
−
−+
+
+
.
Hãy tìm các giá tr ca x bit
rng s hng th 6 trong khai trin này là 224
------------------------------------------------- HT-------------------------------------------------
Thí sinh d thi khi B& D không phi làm câu V.
S GD&T THANH HOÁ
TRNG THPT HU LC 2
THI TH I HC LN I
NM HC 2010 – 2011
MÔN: TOÁN
Thi gian làm bài: 180 phút
S GD&T THANH HOÁ
TRNG THPT HU LC 2
THI TH I HC LN I
NM HC 2010 – 2011
MÔN: TOÁN
Thi gian làm bài: 180 phút
http://laisac.page.tl
ÁP ÁN
JThí sinh làm cách khác úng vn cho im ti a câu ó
- Nu thí sinh làm c hai phn ca phn t chn thì không tính im phn t chn
- Thí sinh thi khi D& B không phi làm câu V. Thang im dành cho câu I.1 và II.2 là
1.5 im
Câu im
1. (1.0 im) Kho sát…
y=x
3
-3x+2
TX D=R
y’=3x
2
-3; y’=0
⇔
1
1
x
x
lim
x
y
→±∞
= ±∞
0,25
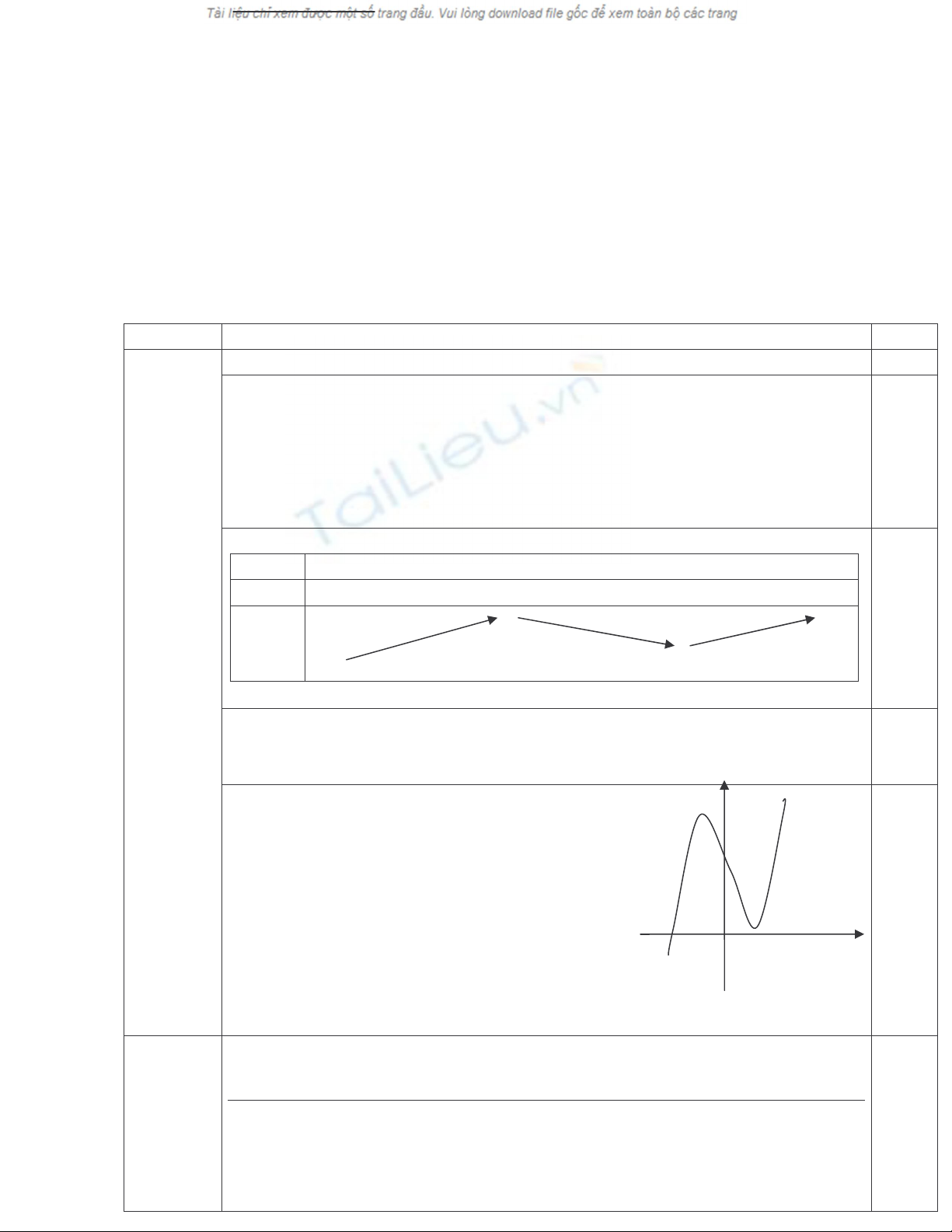
BBT
x
−∞
-1 1
+∞
y’ + 0 - 0 +
y
4
+∞
0
−∞
0,25
Hs ng bin trên khong (
−∞
;-1) và (1;
+∞
), nghch bin trên (-1;1)
Hs t cc i ti x=-1 và y
c
=4, Hs t cc tiu ti x=1 và y
ct
=0
0,25
Câu I.1
(1)
 th : ct Oy ti im A(0;2)
và i qua các im .......
 th nhn im A(0;2) làm tâm i xng
0,25
2(1.
) Vi
2 4
A A
x y
=
=
. Phng trình ng thng
∆
i qua
(
)
Alà
:
(
)
A A
y k x x y
= − +
(
)
: 2 4
y k x
∆ = − +
Lp phng trình hoành  giao im ca (C) và
∆
:
(
)
(
)
(
)
3 2
3 2 2 4 2 2 1 0
x x k x x x x k
− + = − + ⇔ − + − + =
( )
2
2
2 1
x
g x x x k
=
⇔
= + − +
0.25
0.25
S GD&T THANH HOÁ
TRNG THPT HU LC 2
 THI TH I HC LN I
NM HC 2010 – 2011
MÔN: TOÁN
Thi gian làm bài: 180 phút
y
x
i
u ki
n

có BC :
( )
' 0
2 0
g
∆ >
≠
0
9
k
k
>
⇔
≠
.
--------------------------------------------------------------------------------------------------
Khi
ó to

c
a
(
)
(
)
1 1 2 2
; ; ;
B x y C x y
Tho
mãn h
ph

ng trình:
( )
2
2 1 0 (1)
2 4 2
x x k
y kx k
+ − + =
= − +
(
)
2 1
1 2 ' 2
x x k
⇔ − = ∆ =
(
)
(
)
2 1 2 1
2 2
y y k x x k k
⇔ − = − =
----------------------------------------------------------------------------------------------------
Do
ó : Theo gi
thi
t BC=
2 2
3 3
4 4 2 2 4 4 8 0 1
k k k k k
⇔ + = ⇔ + − = ⇔ =
V
y
:
∆
y=x+2
0.25
0.25
1.
K L 
≥−−
>
03loglog
0
2
2
2
2
xx
x
I);-+M);-);-
)1()3(log53loglog
2
2
2
2
2
−>−− xxx
N -=&
O3!"
⇔
)3(5)1)(3()3(532
2
−>+−⇔−>−− tttttt
02.5
0.25
<<
−≤
⇔
<<
−≤
⇔
−>−+
>
−≤
⇔4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
<<
≤<
⇔
168
2
1
0
x
x
P O3M-8  )16;8(]
2
1
;0( ∪
0,25
0.25
3
)
;
0
(
π
∈
x
Q M);-+
cot 1
x
−

xx
x
x2sin
2
1
sin
tan
1
2cos
2
−+
+
K L :
−≠
≠
⇔
≠+
≠
1tan
02sin
0cossin
02sin
x
x
xx
x
L 
xxx
xx
xx
x
xx cossinsin
sin
cos
cos.2cos
sin
sincos
2
−+
+
=
−
⇔
xxxxxx
x
xx cossinsincossincos
sin
sincos
22
−+−=
−
⇔
⇔
)
2
sin
1
(
sin
sin
cos
x
x
x
x
−
=
−
⇔
0)1sincos)(sinsin(cos
2
=−−− xxxxx
0,25
0,25
Câu II
(2.0
im)
⇔
0
)
3
2
cos
2
)(sin
sin
(cos
=
−
+
−
x
x
x
x
⇔
0
sin
cos
=
−
x
x
⇔
tanx = 1
)(
4
Zkkx ∈+=⇔
π
π
(tm)
( )
4
0;0
π
π
==∈xkx
KL:
0,25
0.25
( )
: :

;$  *8
/
/
;$/ /   /
/ / /
/ # #
;$/ # # 3 / # #
/
=
=
=
=
= = =
=
=+ +
=
=
=
= = =
=
=+ +
=
=
=
π π
= ∈ −
= +
=
( )
9 9 9
# #
9
# #
# #
# :
π π π
π
=
=
+π
= = = =
+
0,25
0.25
CâuIII
(1.0
im)
t
( )
2
1
ln( 1)
1
1
2
2
u x
du dx
x
dx
dv v
xx
= +
=
+
=
= −
+
+
.
( ) ( ) ( )
1
0
1
1ln 1 0
2 1 2
dx
x
x x x
− + −
+ + +
= -
1
3
l n2+I
1
I
1
=
1 1 1
0 0 0
1
1 4
ln ln
0
( 1)( 2) 1 2 2 3
dx dx dx x
x x x x x
+
= − = =
+ + + + +
.
Vy I =-
1
3
ln2+ln
4
3
=…
0,25
0.25
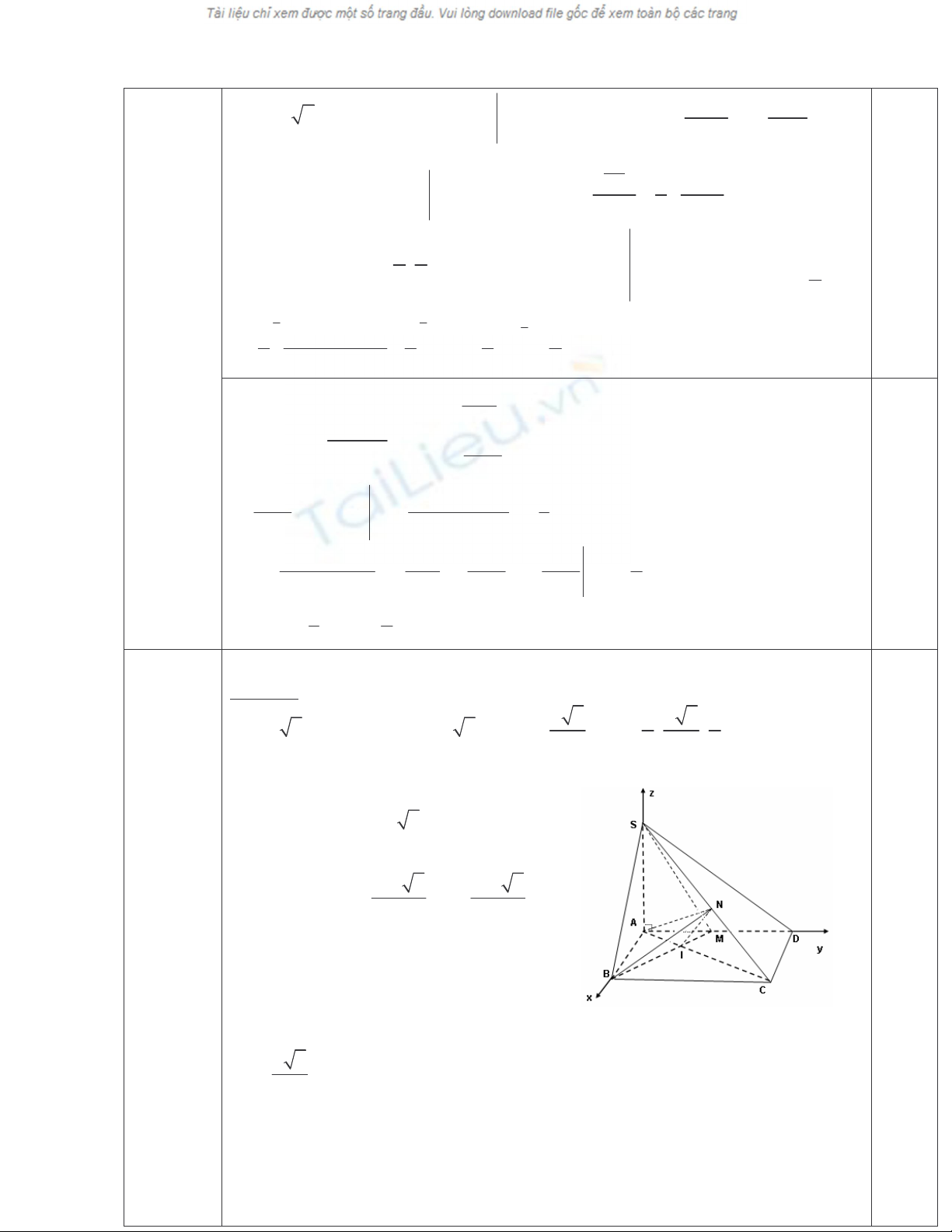
Câu IV
(1.)
 $8+RCF =S)TL  !@@@"!@@"
!@
2
@"!@@" !
2
@"% !@
2
2
a
@"' !
2
; ;
222
a a a
"
JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ
! "U;,V
(
)
2 2
1
, 2; ;0
n AS AC a a
= = −
!% "U;,V
2 2
2
2
2 2
, ; ;
2 2
a a
n SM SB a
− −
= = −
1 2
. 0 ( ) ( )
n n mp SAC mp SMB
=⊥
JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ
E"O);-+)9-<-% 
2
2
0
x a at
a
y t
z
= −
=
=

0,25
0.25
0.25
O);-+)9-<- 
'
2 '
0
x at
y a t
z
=
=
=
 1 2
; ;0
3 3
a
I MB AC I a
= ∩
JJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ
3.4178 ' 0
1
, .
6
ANIB
V AN AB AI
=

2 2 3
1 2 2 2
0. . .0
6 3 3 2 2 36
a a a a a
+ − =
0.25
Câu V
(1.) Gii: Do
( ) ( )( )
xy z xy z x y z x z y z
+ = + + + = + +
ta có:
.
xy x y
xy z x z y z
=
+ + +
Áp dung BT cosi cho hai s :
;
x y
x z y z
+ +
ta !c
1
.2
x y x y
x z y z x z y z
≤ +
+ + + +
.(1)
----------------------------------------------------------------------------------------------------
Lý lun tng t ta c"ng có:
1
2
yz y z
yz x x y x z
≤ +
+ + +
(2)
1
2
xz x z
xz y x y y z
≤ +
+ + +
(3)
---------------------------------------------------------------------------------------------------
Cng v vi v các BT trênvà rút gn ta s !c :
3
2
P
≤
.
Du bng xy ra khi
1
3
x y z
= = =
.
Vy P t giá tr ln nht bng
3
2
khi
1
3
x y z
= = =
.
0.5
0.25
0.25
Chng trình chu#n
Câu
VIA
(2.0
im)
1.
(1.0 im)
Theo gi thit : B
∈
∆
1
⇔
B(a; 3 –a) . C
∈
∆
2
⇔
C(b; 9-b)
0.25