TRƯỜNGTHPTCHUYÊNVĨNHPHÚC KỲTHITHỬĐẠIHỌCLẦN1NĂMHỌC20122013
Môn:Toán12.Khối A.
Thờigianlàmbài:150phút(Khôngkểthờigiangiaođề)
A.PHẦNCHUNGCHOTẤTCẢTHÍSINH(8,0điểm)
Câu I(2,5điểm)Chohàmsố: 3 3 2y x mx = - +
( )
1 ,m lµ tham sè thùc.
1)Khảosátsựbiếnthiênvàvẽđồthịhàmsố
( )
1 khi1m =
2) T×m c¸c gi¸ trÞ cña m ®Ó ®å thÞ hµm sè
( )
1 cã tiếptuyếntạovớiđườngthẳng : 7 0d x y + + = góc
a,biết 1
cos 26
a =.
CâuII(2,5điểm)1)Giảiphươngtrình:
4
3 4cos2 8sin 1
sin 2 cos 2 sin 2
x x
x x x
- - =
+
2) Giảihệphươngtrình:
( )
3 3
2 2
4 16
1 5 1
x y y x
y x
ì + = +
ï
í + = +
ï
î
( , )x y ÎR .
CâuIII(1,0điểm)Tính giớihạn :
3 2
2
2
6 4
lim 4
x
x x
L x
®
- - +
= -
CâuIV.(1,0điểm)Chohìnhlậpphương 1 1 1 1
.ABCD A B C D cãđộdàicạnhbằng 3 vàđiểmMthuộccạnh
1
CC saocho 2CM =.Mặtphẳng
( )
ađiqua ,A M vàsongsomgvớiBDchiakhốilậpphươngthànhhai
khốiđadiện.Tínhthểtíchhaikhốiđadiệnđó.
CâuV.(1,0điểm)Chocácsốthực , ,x y zthoảmãn 2 2 2 3x y z + + = .Tìmgiátrịlớnnhấtcủabiểuthức:
2 2
3 7 5 5 7 3F x y y z z x = + + + + +
B.PHẦNRIÊNG (2,0điểm).Thísinhchỉđượclàmmộttronghaiphần(phần1 hoặc2)
1.TheochươngtrìnhChuẩn
CâuVIa.(1,0 điểm)Trongmặtphẳngvớihệtoạđộ Oxy cho hai ®iÓm
( ) ( )
2;1 , 1; 3A B - - vµ hai ®êng
th¼ng1 2
: 3 0; : 5 16 0.d x y d x y + + = - - = T×m to¹ ®é c¸c ®iÓm ,C D lÇn lît thuéc1 2
,d d sao cho tø gi¸c
ABCD lµ h×nh b×nh hµnh.
CâuVIIa.(1,0 điểm)Tínhtổng: 2 1 2 2 2 3 2 2012
2012 2012 2012 2012
1 2 3 2012S C C C C = + + + + L
2.TheochươngtrìnhNângcao
CâuVIb.(1,0 điểm)TrongmặtphẳnghệtoạđộOxy choelíp
( )
2 2
: 1
9 4
x y
E + = vµ c¸c ®iÓm
( )
3;0A - ;
( )
1;0I - .T×m to¹ ®é c¸c ®iÓm ,B C thuéc
( )
E sao cho I lµ t©m ®êng trßn ngo¹i tiÕp tam gi¸cABC
CâuVIIB:(1,0điểm):Tínhtổng:
0 1 2 2012
2012 2012 2012 2012
1 2 3 2013
C C C C
T = + + + + L
HẾT
Ghichú: Thísinhkhôngđượcsửdụngbấtcứtàiliệugì!
Cánbộcoithikhônggiảithíchgìthêm!
Cảm ơnthầyNguyễnDuyLiên(lientoancvp@vinhphuc.edu.vn)gửitớihttp://www.laisac.page.tl/
Đềchínhthức
(Đềthigồm01trang)
TRƯỜNGTHPTCHUYÊNVĨNHPHÚCĐÁPÁNĐỀTHITHỬĐẠIHỌCNĂM20122013–LẦN1
MÔNTOÁN–KHỐIA
(Đápángồm5trang)
Câu Nộidungtrìnhbày Điểm
I(2,0đ) 1.(1,50điểm)
Khi 1m =hàmsố(1)códạng 3 3 2y x x = - +
a)TậpxácđịnhD = ¡
b)Sựbiếnthiên
+)Chiềubiếnthiên: 2
' 3 3y x = - , ' 0 1y x = Û = ±.Khiđóxétdấucủa 'y:
+ +
0
0
11 +¥
¥
y
x
hàmsốđồngbiếntrênkhoảng
( ) ( )
; 1 , 1; -¥ - + ¥vànghịchbiếntrênkhoảng
( )
1;1 -.
0,50
+)Cựctrị:hàmsốđạtcựcđạitại 1, 4
CD
x y = - =
Hàmsốđạtcựctiểutại 1, 0
CT
x y = =
+)Giớihạn: 3 3
2 3 2 3
3 2 3 2
lim lim 1 ; lim lim 1
x x x x
y x y x
x x x x
®-¥ ®-¥ ®+¥ ®+¥
æ ö æ ö
= - + = -¥ = - + = +¥
ç ÷ ç ÷
è ø è ø
0,25
+)Bảngbiếnthiên:
:
x -¥ 1 1 +¥
y' + 0 -0 +
y
4 +¥
-¥ 0
0,25
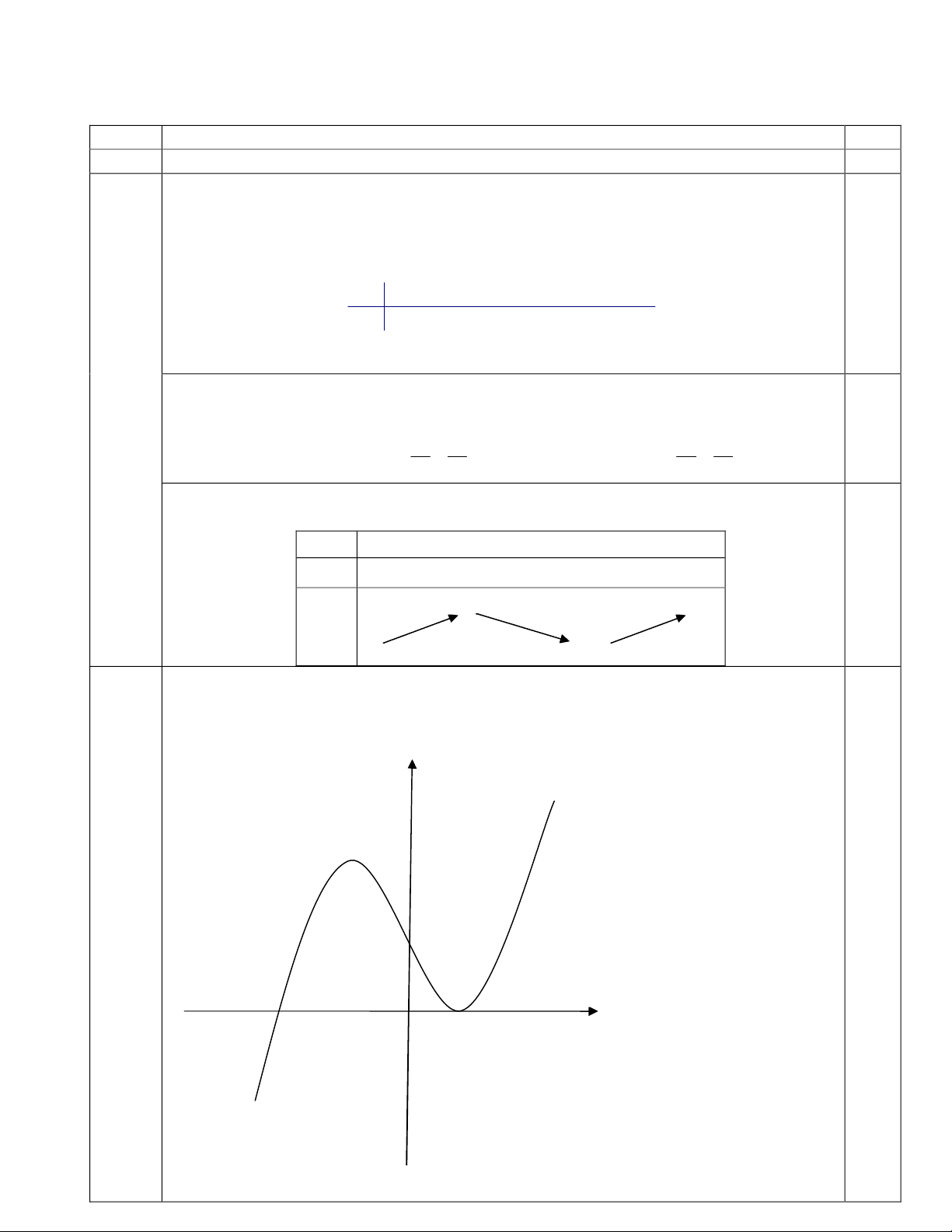
c)Đồthị: 3
0 3 2 0 1, 2y x x x x = Û - + = Û = = - ,suyrađồthịhàmsốcắttrụcOxtạiOx
tạicácđiểm
( ) ( )
1;0 , 2;0 -
'' 0 6 0 0y x x = Û = Û = Þđồthịhàmsốnhậnđiểm
( )
0;2 làmđiểmuốn.
0,50
1
1
4
x
0
y
2.(1,0 điểm)
Gọiklàhệsốgóccủatiếptuyến Þtiếptuyến cóVTPT
( )
1 ; 1n k = -
r
Đườngthẳng : 7 0d x y + + = tiếptuyến cóVTPT
( )
2 1;1n =
r0,25
Tacó
( )
1 2
1 2 2
1 2
1
1
cos cos , 26 2 1
n n k
n n n n k
× -
a = = Û = +
r r
r r r r2 3 2
12 26 12 0 2 3
k k k k Û - + = Û = Ú =0,25
YCBTthoảmãn Ûítnhấtmộttronghaiphươngtrìnhsaucónghiệm:
, 2 2
, 2 2
3 3 2 1 2 1
3 3 0
2 2 2 2
2 2 9 2 9 2
3 3 0
3 3 9 9
m m
y x m x
m m
y x m x
+ +
é é é é
= - = = ³
ê ê ê ê
Û Û Û
ê ê ê ê
+ +
ê ê ê ê
= - = = ³
ê ê ê ê
ë ë ë ë
1
2
2
9
m
m
é ³ -
ê
ê
ê ³ -
ê
ë
1
2
m Û ³ -0,25
Vậyđểđồthịcótiếptuyếntạovớiđườngthẳng : 7 0d x y + + = góc a ,có 1
cos 26
a =.
thì
1
2
m³ -
0,25
II(2,5đ)1.(1,25 điểm).Giảiphươngtrình:
4
3 4cos2 8sin 1
sin 2 cos 2 sin 2
x x
x x x
- - =
+
§/k
( )
sin 2 cos 2 0 8 2
sin 2 0
2
x l
x x l
x x l
p p
p
ì ¹ - +
ï
+ ¹
ì ï
Û Î
í í
¹
î ï ¹
ï
î
Z0,25
ta cã:
2
4 1 cos 2
8sin 8 3 4 cos 2 cos 4
2
x
x x x
-
æ ö
= = = - +
ç ÷
è ø L
Ph¬ng tr×nh
( )
3 4 cos2 3 4cos 2 cos 4 1
sin 2 cos 2 sin 2
x x x
x x x
- - - +
Û =
+
( )
cos 4 1 sin 2 cos 2 0,sin 2 0
sin 2 cos 2 sin 2
x do x x x
x x x
-
Û = + ¹ ¹
+
0,50
( ) ( )
1
cos 2 sin 2 cos 2 sin 2 cos 2 0
sin 2
x x x x x
x
Û - - = Û + =
( )
( )
cos2 0 sin 2 cos2 0 2 2
4 2
x x x loai x k
x k k
p p
p p
Û = Ú + = Û = +
Û = + ΢
0,25
VËy ph¬ng tr×nh cã mét hä nghiÖm
( )
4 2
x k k
p p
= + ÎZ0,25
2.(1,25điểm).Giảihệphươngtrình:
( )
3 3
2 2
4 16
1 5 1
x y y x
y x
ì + = +
ï
í + = +
ï
î
( , )x y ÎR .
Viếtlạihệphươngtrình:
( )
3 3
2 2
4 4 0(*)
5 4(**)
x y x y
y x
ì + - - =
ï
í - =
ï
î
Thay
( )
** vào
( )
* tađược:
( )
( )
3 2 2 3 3 2 2
5 4 0 21 5 4 0x y x y x y x x y xy + - - - = Û - - =
0,25
![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)
![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)
