SỞ GD – ĐT TT HUẾ
TRƯỜNG THPT HƯƠNG LÂM
ĐỀ THAM KHẢO, THI HỌC KỲ II NĂM HỌC 2008-2009.
Giáo viên: Ngô Huế.
Đề: Toán. Thời gian: 150’
I. Phần chung cho tất cả các thí sinh (7điểm).
Câu 1: (3 điểm).
Cho hàm số:
42
1
x
yx
.
1/ Khảo sát sự biến thiên và vẽ đồ thị của hàm số trên.
2/ Viết phương trình tiếp tuyến với đồ thị của hàm số trên tại điểm có hoành độ
x0 = 1.
Câu 2: ( 3 điểm)
1/ Tìm GTLN, GTNN của hàm số f(x) = x3 +2x2-7x trên đoạn [-1; 2].
2/Giải phương trình sau:
232
21
xx
.
3/ Tính:
2
1
ln
e
x xdx
.
Câu 3: (1 điểm)
Cho khối lăng trụ tam giác ABC.A’B’C’. Tính tỷ số:
. ' ' '
. ' '
C A B C
C ABB A
V
V
.
II. Phần riêng: (3 điểm)
*Theo phương trình chuẩn:
Câu 4: (2 điểm) Trong không gian với hệ toạ độ Oyxz. Cho điểm A=(1; 2; 3) và
điểm B=(2; -3; 4).
1/ Viết phương trình mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng
AB.
2/Trong mặt phẳng (P) cho điểm C= (2; 0 ; -8). Viết phương trình tham số của
đường thẳng đi qua điểm B và song song với đường thẳng AC.
Câu 5: (1 điểm)
Cho hai số phức: z1 = 5 + 2i ; z2 = 3 – 5i .
Hãy tìm:
12
zz
.
Hướng dẫn chấm:
Câu
Mục
Nội dung
1
1
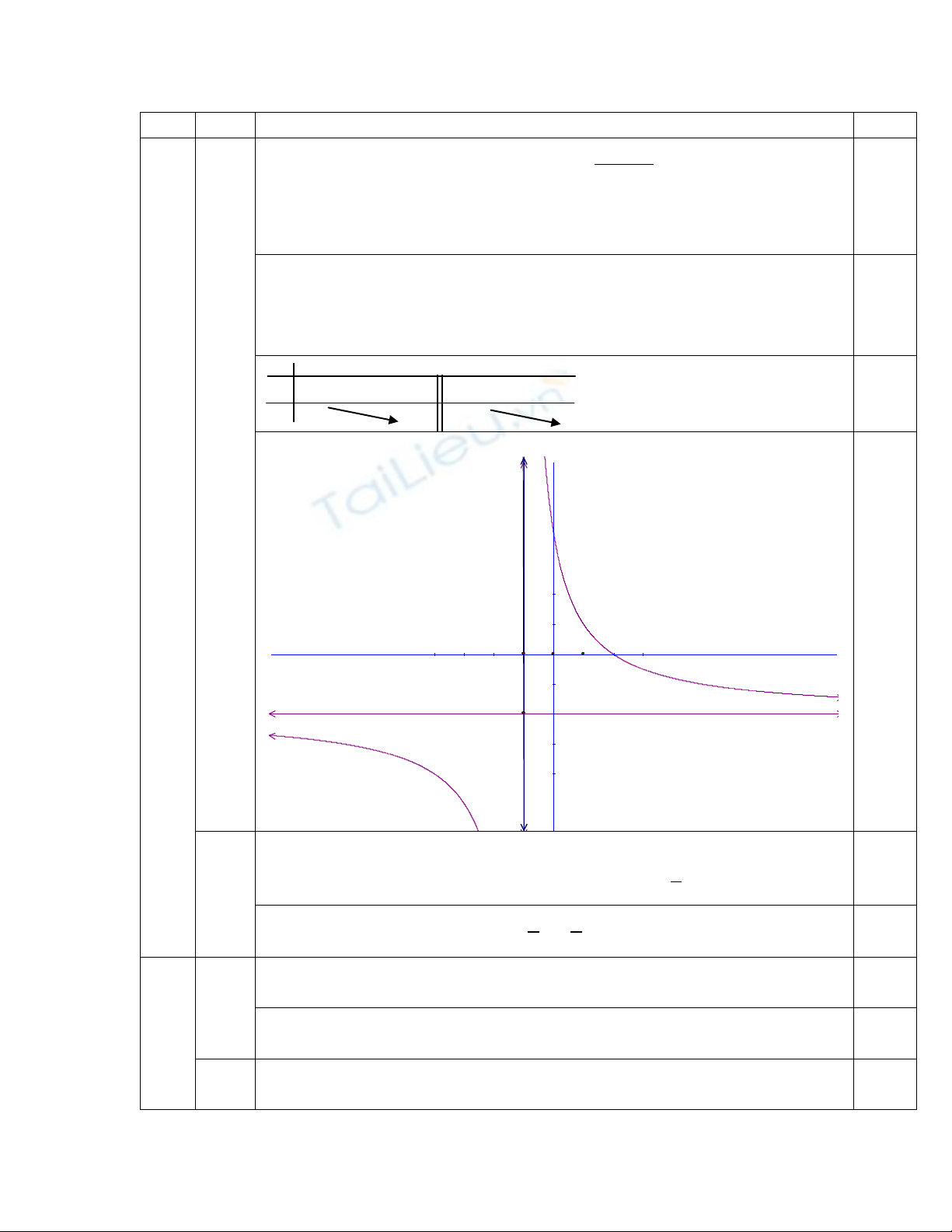
Tập xác định:
1D
;
2
6
'( ) 1
fx x
< 0;
=> hàm số nghịch biến trên các khoảng:
; 1 1;
;
không có cực trị.
11
lim ( ) ; lim ( )
xx
f x f x

 
Đồ thị của hàm số có tiệm
cận đứng là: x = 1.
lim ( ) 2.
xfx

Đồ thị của hàm số có tiệm
cận ngang là: y = -2.
x

-1

y’ - -
y -2


-2
Vẽ đồ thị:
x
y
1
2
Phương trình tiếp tuyến với đồ thị tại điểm có x0 = 1; có dạng :
y - y0 = f’(x0)(x – x0). Ta có: y0 = 1; f’(x0) =
3
2
.
Vậy PT tiếp tuyến đó là: y =
35
22
x
.
2
1
Tập xác định của hs là: R. f’(x) = 3x2 +4x -7; f’(x) = 0 x1 = 1;
x2 = -7/3 (bị loại ); f(-1) = 8 ; f(1) = -4 ; f( 2) = 2.
Vậy:
1;2
1;2
ax ( ) ( 1) 8;min ( ) (1) 4m f x f f x f
.
2
23 2 0 2 12
2 2 3 2 0 1; 2.
xx
pt x x x x

3
u = lnx ; x2 dx = dv => du =1/x dx ; v = x3/3.
I =
32
2
1
11
ln ln
33
ee
e
xx
x xdx x dx

.
I =
3
33
1
21
3 9 9 9
e
e x e
.
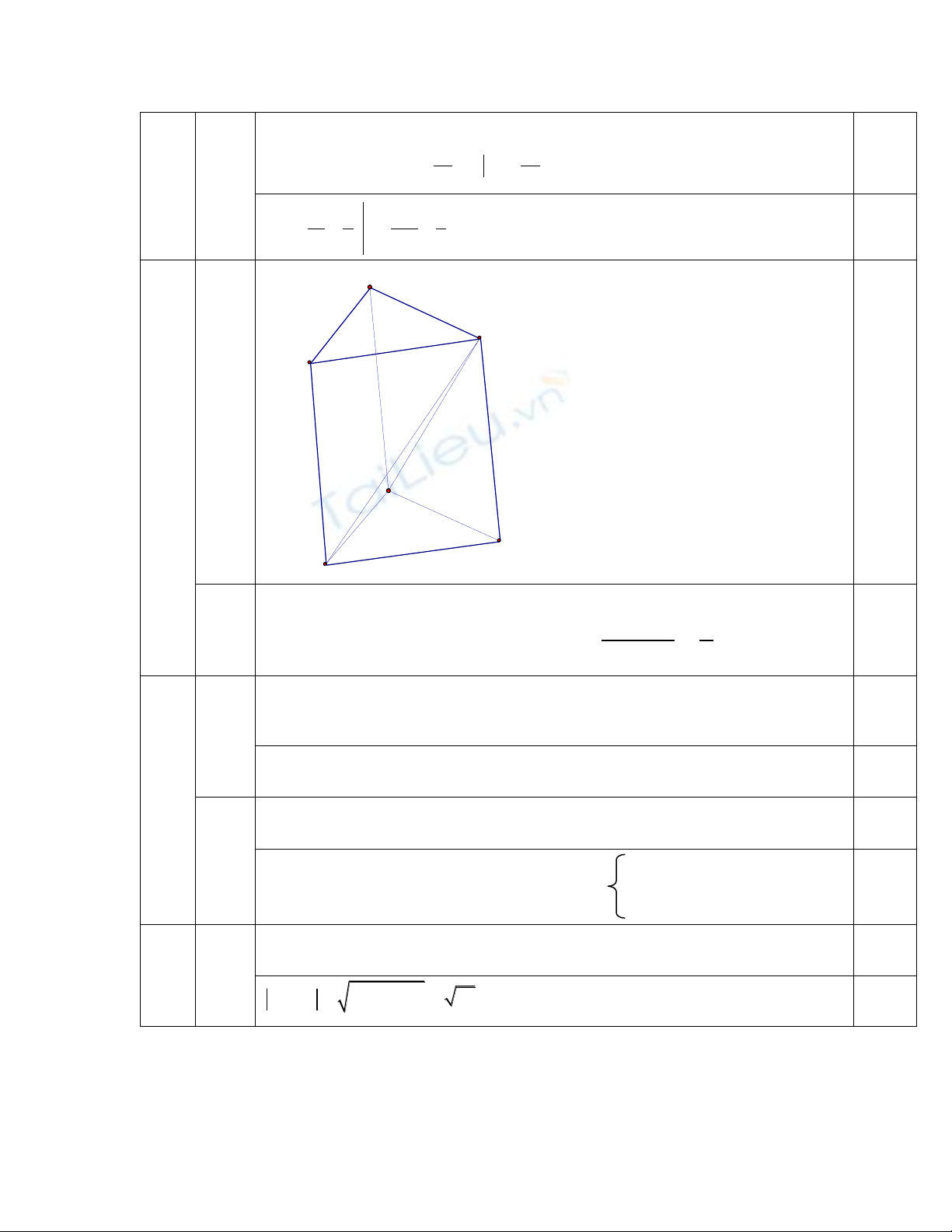
3
A
A'
B
C
C'
B'
vẽ hình
Gọi thể tích của khối lăng trụ ABC.A’B’C’ là V, ta có VC.A’B’C’
=1/3 V ; => VC.ABB’A’ =2/3 V => Vậy:
. ' ' '
. ' '
1
2
C A B C
C ABB A
V
V
.
4
1
Mặt phẳng (P) nhận véc tơ
(1; 5;1)AB 
làm véc tơ ph tuyến,
vậy phương trình mp(P) là: (x – 1 ) - 5( y – 2 ) + (z – 3) = 0.
Vậy PT mp(P) là: x – 5y + z + 6 = 0.
2
Đường thẳng đi qua điểm B và song song với AC nhận véc tơ
AB
= ( 1 ; - 2 ; -11 ) làm véc tơ chỉ phương.
Vậy Pt tham số của đường thẳng đó là: x = 2 +t
y = -3 -2t (t: tham số).
z = 4 – 11t
5
z1 + z2 = 8 – 3i
2
2
12 8 3 73zz