TRƯỜNG THPT CHUYÊN HẠ LONG ðỀ THI THỬ ðẠI HỌC LẦN THỨ HAI
------------------------------- Năm học 2009 – 2010
Môn thi: TOÁN (Khối D)
Thời gian làm bài: 180 phút
A. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 ñiểm)
Câu I (2 ñiểm )
Cho hàm số y =
1
x
x
−
(1)
1. Khảo sát sự biến thiên và vẽ ñồ thị (C) của hàm số (1).
2. Viết phương trình tiếp tuyến d của (C) sao cho d và hai ñường tiệm cận của (C) cắt nhau tạo
thành một tam giác vuông cân.
Câu II (2 ñiểm )
1. Giải phương trình: 3 – tanx (tanx + 2sinx) + 6cosx = 0.
2. Tìm m ñể hệ phương trình:
2 0
1
x y m
x xy
− − =
+ =
có nghiệm duy nhất.
Câu III (1 ñiểm) Tính tích phân:
2
3
1
1
dx
Ι =
+
∫
Câu IV (1 ñiểm)
Cho một lăng trụ ñứng ABC.A’B’C’ có ñáy ABC là tam giác vuông, AB = AC = a, AA’ = a
2
.
Gọi M, N lần lượt là trung ñiểm của ñoạn AA’và BC’. Chứng minh MN là ñường vuông góc chung
của các ñường thẳng AA’và BC’. Tính thể tích của khối tứ diện MA’BC’.
Câu V (1 ñiểm)
Giải phương trình : 2
2 1
log 1 2
x
x
x
x
−
= + −
B. PHẦN RIÊNG (3 ñiểm)
Thí sinh chỉ ñược làm một trong hai phần (phần 1 hoặc phần 2)
Phần 1: Theo chương tình chuẩn
Câu VI.a (2 ñiểm)
1. Trong mặt phẳng với hệ toạ ñộ Oxy, tìm toạ ñộ các ñỉnh của tam giác ABC biết rằng ñường
thẳng AB, ñường cao kẻ từ A và ñường trung tuyến kẻ từ B lần lượt có phương trình là x + 4y – 2 = 0,
2x – 3y + 7 = 0, 2x + 3y – 9 = 0.
2. Trong không gian với hệ toạ ñộ Oxyz cho hai ñiểm I(0;0;1), K(3;0;0). Viết phương trình mặt
phẳng ñi qua hai ñiểm I, K và tạo với mặt phẳng (xOy) một góc bằng
0
30
Câu VII.a (1 ñiểm) Kí hiệu
k
n
C
là số tổ hợp chập k của n phần tử ( , ;
k n N k n
∈ ≤
). Chứng minh ñẳng
thức: 0 2 2 4 4 2 2 2 1 2
2 2 2 2
.3 .3 ... .3 2 (2 1)
n n n n
n n n n
C C C C −
+ + + + = +
Phần 2: Theo chương trình nâng cao
Câu VI.b (2ñiểm)
1. Trong mặt phẳng với hệ toạ ñộ Oxy, cho ñường tròn (C): 2 2
1.
x y
+ =
ðường tròn tâm (C’) tâm
I(2;2) cắt (C) tại hai ñiểm A, B sao cho AB =
2
. Viết phương trình ñường thẳng AB.
2. Trong không gian với hệ toạ ñộ Oxyz cho ñiểm I(2;2;-2) và mặt phẳng (P): 2x + 2y + z + 5 = 0.
a. Lập phương trình mặt cầu (S) có tâm là I sao cho giao của (S) và (P) là ñường tròn (C) có chu
vi bằng
8
π
b. Tìm toạ ñộ tâm của ñường tròn (C)
Câu VII.b (1 ñiểm) Cho tập X gồm tất cả các số tự nhiên có 3 chữ số khác nhau
( , , 6)
abc a b c
<
.Chọn
ngẫu nhiên một số trong X. Tính xác suất ñể kết quả chọn ñược là một số chia hết cho 3.
------------------------Hết---------------------
TRƯỜNG THCS & THPT NGUYỄN KHUYẾN ĐỀ THỬ SỨC ĐẠI HỌC 2010
LỚP 12D1 Môn thi: Toán
 Thời gian: 180 phút
Đ
Ề
S
Ố
027
http://www.VNMATH.com
http://www.VNMATH.com
27
http://www.VNMATH.com
TRƯỜNG THPT CHUYÊN HẠ LONG ðÁP ÁN VÀ BIỂU ðIỂM
------------------------------- ðỀ THI THỬ ðẠI HỌC LẦN THỨ HAI
Năm học 2009 – 2010
Môn thi : TOÁN ( khối D)
Câu Nội dung ðiểm
I
2ñ’
1
1ñ’
• TXð:
{
}
\ 1
D R=
• Sự biến thiên
.
( )
2
1
' 0
1
y
x
= − <
− với
x D
∀ ∈
.H/s nghịch biến trên các khoảng
(
)
(
)
;1 , 1;
−∞ +∞
và không có cực trị
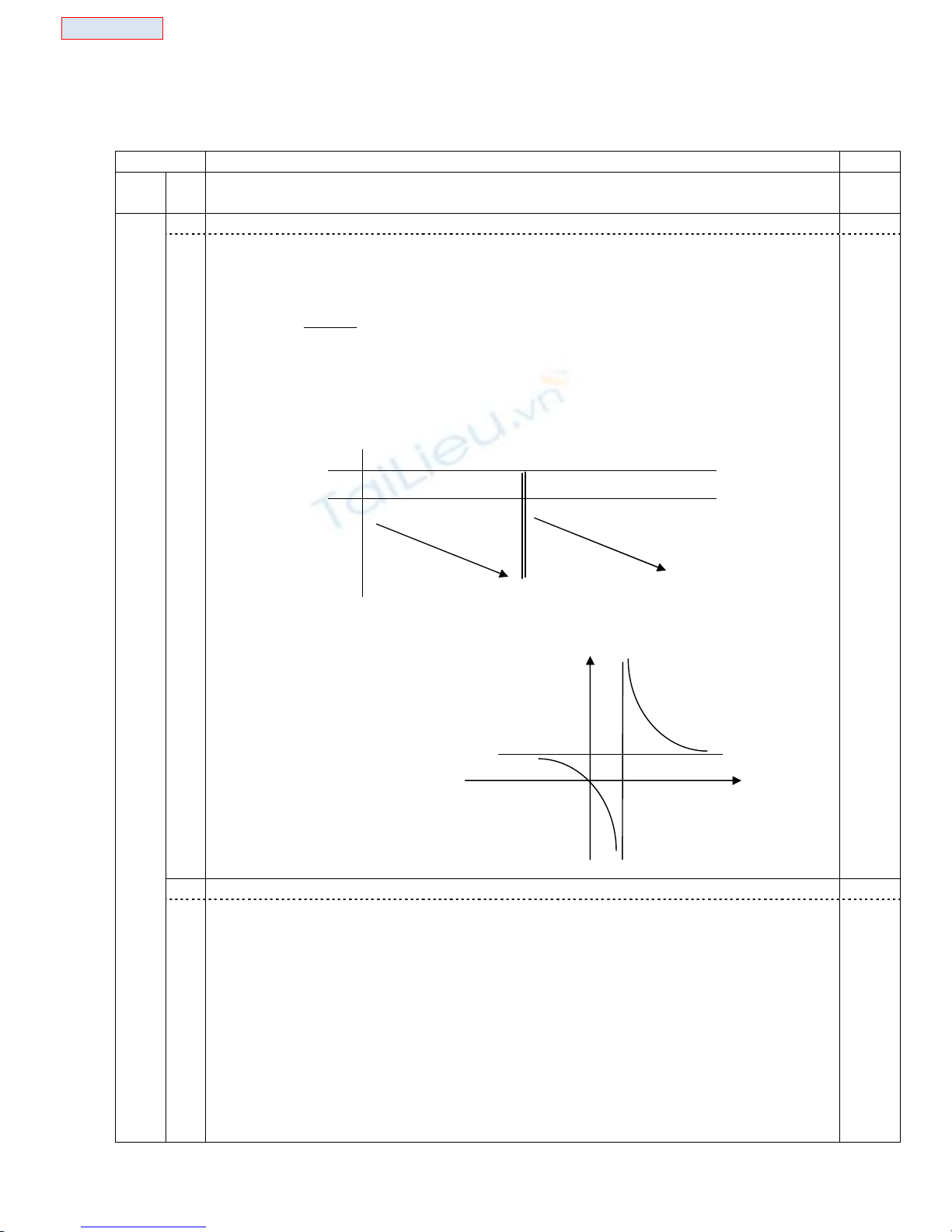
.Tìm ñược tiệm cận ñứng :x=1 ,tiệm cận ngang :y=1
◦ Bảng biến thiên:
x
−∞
1
+∞
y’
_
_
y 1
−∞
+∞
1
• ðồ thị:
.ðồ thị nhận ñiểm I(1;1) là tâm ñối xứng và qua O(0;0)
0,25
0,25
0,25
0,25
2
1ñ’
• ðồ thị (C) có 2 ñường tiệm cận vuông góc với nhau ,trong ñó có 1tiệm cận song
song với trục Ox nên YCBT
⇔
lập pt tiếp tuyến cúa (C) sao cho tt hợp với Ox 1
góc
0
45
và không ñi qua giao ñiểm 2 ñương tiệm cận
• Lập luận ñể có hệ số góc của tt là k=1 hoặc k=-1
• Xét k=1 : pt hoành ñộ tiếp ñiểm là y’=1 vô nghiệm nên không có tt
• Xét k=-1: pt hoành ñộ tiếp ñiểm là ,
0
1
2
x
yx
=
= − ⇔
=
0 0, :
2 2, : 4
x y pttt y x
x y pptt y x
=⇒= = −
=⇒= = − +
(Tmãn không qua giao ñiểm 2 ñường tiệm cận )
LK:Có 2 pttt cần tìm :y=-x và y=-x+4
0,25
0,25
0,25
0,25
1
1 x
y
O
Đ
Ề
S
Ố
027
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
109
http://www.VNMATH.com
1
1ñ • ðk: Cos x
≠
0 (*) Khi ñó
( )
( )
2
2
2
2
sin 1 2 osx
3 1 2 osx 0
osx osx
sin
1 2 osx 3 0
os x
-1
osx= ( )
2
tan 3
( )
3
x c
pt c c c
x
cc
ctmdk
x
x k k Z
ππ
+
⇔ + − =
⇔ + − =
⇔=
⇔ = ± + ∈
0,25
0,25
0,25
0,25
II
(2ñ’)
2
1ñ’
• Hệ pt ñã cho
( ) ( )
2 2
1 0 1
2 2 (1)
2 1 0(2)
1
x x
y x m y x m
x m x
xy x
− ≥ ≤
⇔ = − ⇔ = −
+ − − =
= −
• Yêu cầu bài toán
(2)
pt
⇔
có ñúng 1 nghiệm thoả mãn x
1
≤
(*)
• Ta có pt(2)có 2 nghiệm trái dấu với
m
∀
(do a.c <0 )
(*) (2)
pt
⇒⇔
có 2nghiệm
2
1 2
(2 ) (2 ) 4
1 1
2
..... 2
m m
x x
m
− − + − +
< < ⇔ >
⇔ >
0,25
0,25
0,5
III
(1ñ’)
• Tính I=
2 2 2
3 3 3
1 1
1 1
dx x dx
x x x x
=
+ +
∫ ∫
• ðặt
3 2
1 2 3
1 2, 2 3
x t tdt x dx
x t x t
+ = ⇒=
=⇒= = ⇒=
•
3 3
2
2 2
3
2
1 1 1 1
3 1 3 1 1
1 1 1 1 2 1 1 3 2 2
ln ln ln ln
3 1 3 2 3 2
2 1
dt
I dt
t t t
t
t
⇒= = −
− − +
− − +
= = − =
++
∫ ∫
0,25
0,25
0,25
0,25
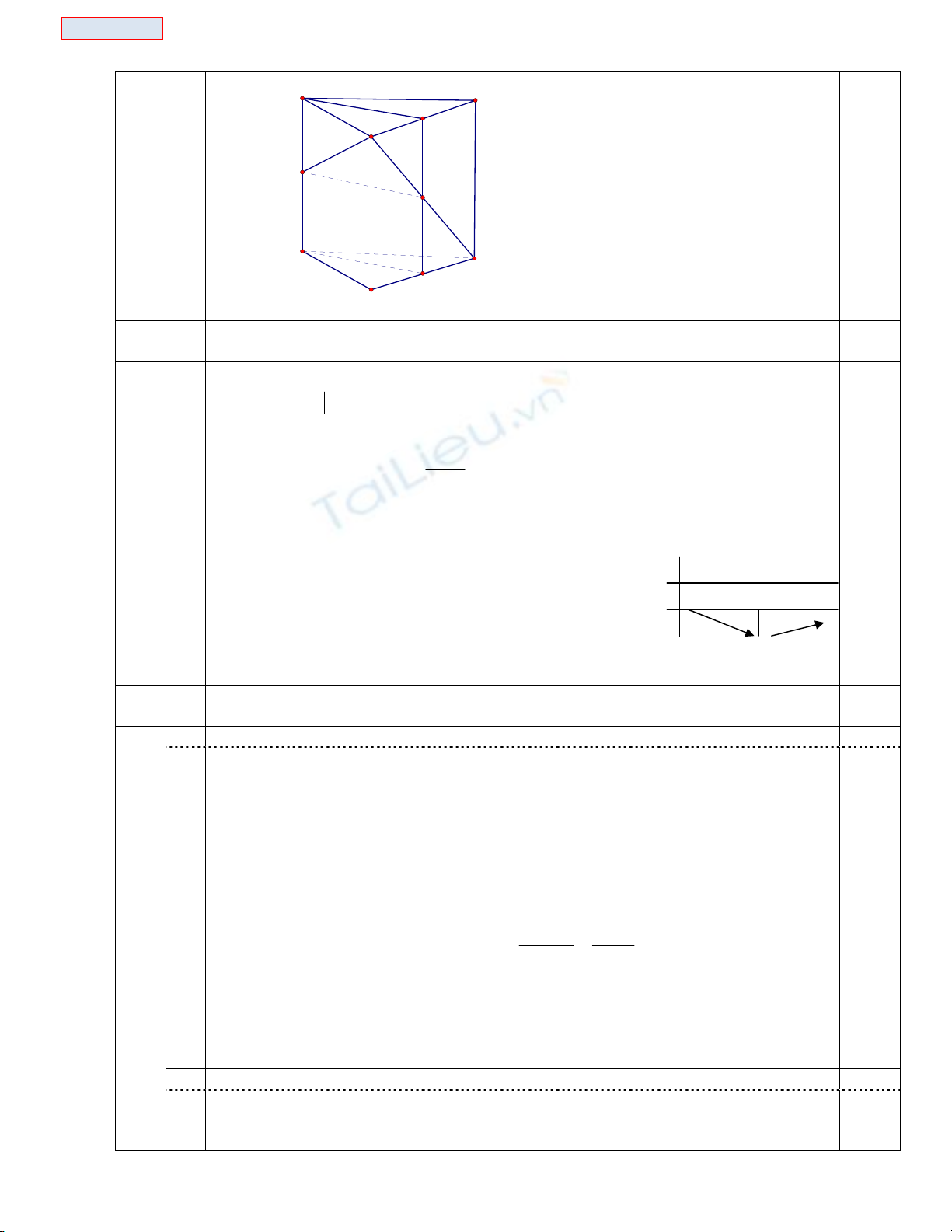
VI
(1ñ’)
• NM cắt AA’ tại M và BB’ tại N, gọi H,K lần lượt là trung ñiểm của BC và
B’C’ ta có H,N,K thẳng hàng
+Lập luận ñể có MNKA’ là hcn
'
MN AA
⇒⊥
tại M
+ Lập luận ñể có
'
MN BC
⊥
tại N
• +Lập luận ñược AB là ñường cao của chóp B.A’MC’
+Tính ñược diện tích tam giác A’MC’= 2
2
4
a
( )
32
12
a
V dvtt
⇒=
0,25
0,25
0,25
0,25
Đ
Ề
S
Ố
027
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
110
http://www.VNMATH.com
N
A
A'
B'
C'
B
C
H
K
M
V
(1ñ’)
• ðk
2 1 0
0
0
x
xx
x
−>
⇔ >
≠
• Với ðk trên pt
( )
2 2 2
2 1
log 1 2 log 2 1 2 1 log
x
x x x
x x x
x
−
⇔ = − + ⇔ − + − = +
(1)
• 2
( ) log
f t t t
= +
là h/s ñòng biến trên
(
)
0;
+∞
nên
(
)
(
)
1 2 1 2 1 2
. , 0
f t f t t t t t
= ⇔ = ∀ >
(1)
2 1 2 1 0
x x
x x
⇔ − = ⇔ − − =
(2) x 0 x
0
+
∞
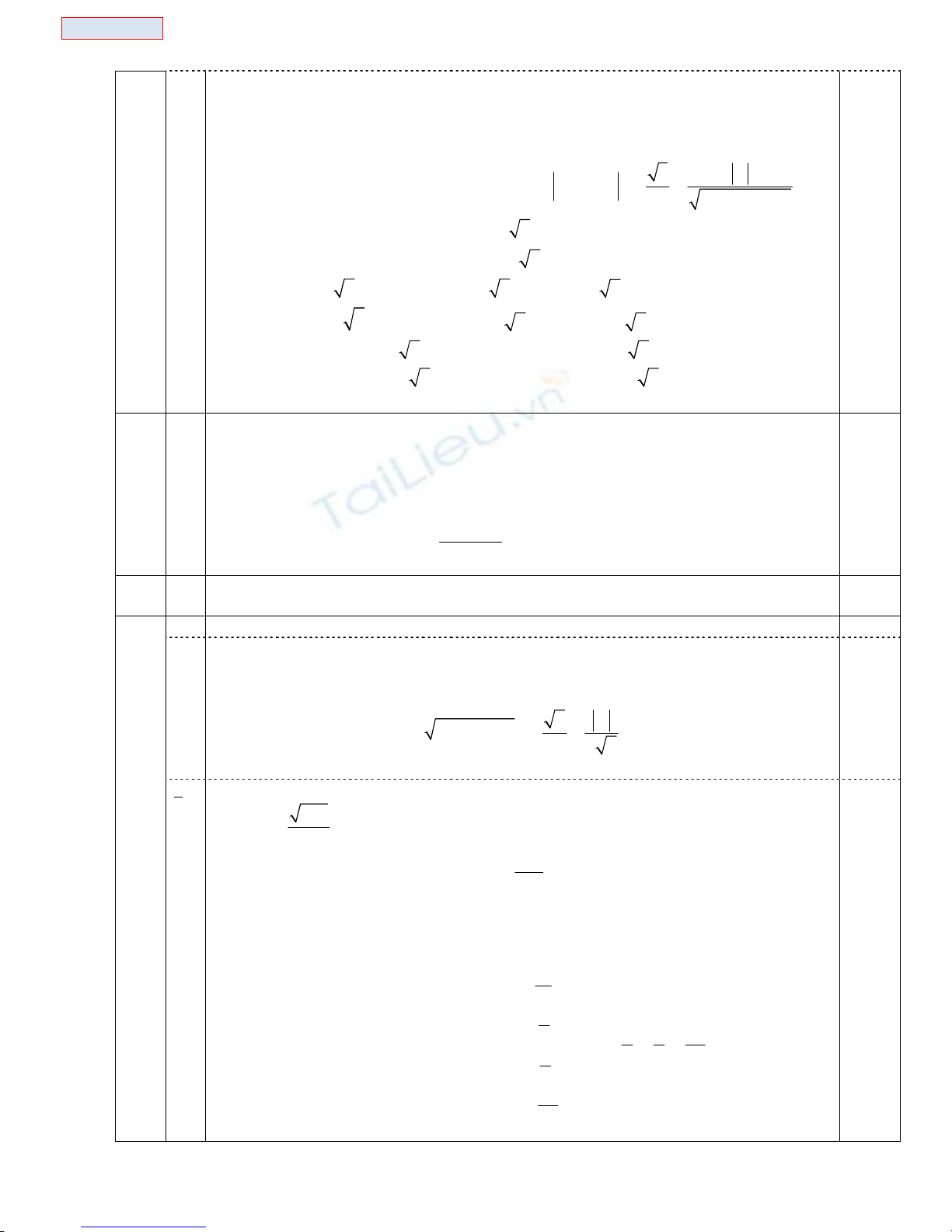
• ðặt
(
)
2 1
x
g x x
= − −
,xét CBT của g(x) trên(0;
)
+∞
g’ - 0 +
g’=
(
)
2 2 0
2 ln 2 1 0 log log
x
x e x
− = ⇔ = =
, g(0)=0 g
Từ BBT ta có pt(2) có tối ña 1 nghiệm x>0 .Ta có x=1 là nghiệm c
ủa pt(2)
KL :pt ñã chocó 1 nghiệm duy nhất x=1
0,25
0,25
0,25
0,25
Via
(2ñ’)
1
1ñ’
• Toạ ñộ A là nghiệm của hệ
( )
4 2 0 2
2;1
2 3 7 0 1
x y x A
x y y
+ − = = −
⇔⇒−
− + = =
• Toạ ñộ B là nghiệm của hệ
( )
4 2 0 6
6; 1
2 3 9 0 1
x y x B
x y y
+ − = =
⇔⇒−
+ − = = −
• .Lập luận ñể có pt của BC:3x+2y-16=0
.M là trung ñiểm của AC
2
2 2
1
2 2
A C C
M
A C C
M
x x x
x
y y y
y
+ − +
= =
⇔+ +
= =
,Lại có M thuộc trung
tuyến qua B nên :
2 3 19 0
C C
x y
+ − =
• Toạ ñộ của C thoả mãn
( )
3 2 16 0 2
2;5
2 3 19 0 5
x y x C
x y y
+ − = =
⇔⇒
+ − = =
0,25
0,25
0,25
0,25
2
1ñ’
• Giảsử
(
)
; ;
n A B C
r
làvéctơ pháp tuyến của mp’(P) cần tìm (A,B,C không ñồng
thời =0)
Đ
Ề
S
Ố
027
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
111
http://www.VNMATH.com
.Vì
, ( )
(3;0; 1) . 0 3 0 3
( )
K I P
IK IK n A C C A
n P
∈
−⇒= ⇔ − = ⇔ =
⊥
uur uur r
r(1)
• (P) hợp với (xOy) 1góc
0
30
0
2 2 2
3
os30 os(n, ) (2)
2
C
c c k
A B C
⇔ = ⇔ =
+ +
r r
• Từ (1) và (2) 2 2
2
2
2
B A
A B
B A
=
⇒= ⇔
= −
.
.Với
2
B A
= chọn A=1
⇒
B=
2
,C=3
(1; 2;3)
n⇒
r
.Với
2
B A
=− chọn A=1
⇒
B=-
2
,C=3
(1; 2;3)
n⇒−
r
• mp’có vtơ pt
n
r
và qua I(0;0;1) có pt:
2 3 3 0
x y z
+ + − =
mp’có vtơ pt
(1; 2;3)
n−
r
và qua I(0;0;1) có pt:
2 3 3 0
x y z
− + − =
Cả 2 mp’ có pt trên thoả mãn qua K và là mp’ cần tìm
0,25
0,25
0,25
0,25
VIIa
(1ñ’)
•
( )
( ) ( )
2
2
2
2
0
2
2
2
2
0
4 1 3 3
2 1 3 1 3
n
n
n k k
n
k
n
n k
n k k
n
k
C
C
=
=
= + =
= − = −
∑
∑
Với
,
,
k n
k n N
≤
∈
•
2 2
0 2 2 2 1 2
2 2 2
4 2
... 2 (2 1)
2
n n
n n n
n n n
C C C −
+
⇒+ + + = = +
0,25
0,25
0,5
VIb
(2ñ)
1
1ñ’
• ðường tròn (C) có tâm O(0;0) và bán kính R=1 ,ñường tròn (C’) cắt (C) tại A,B
nên
AB OI
⊥
tại H là trung ñiểm của AB suy ra
(2;2)
OI
uur
là véc tơ pháp tuyến
Pt AB có dang :2x+2y+C=0
• 2 2 2
( , ) 2
22 2
C
d O AB OH OB HB C
= = − ⇔ = ⇔ = ±
• KL: x+y+1=0 và x+y-1=0 là pt ñường thẳng cần tìm
0,25
0,5
0,25
2
1ñ’
• Lập luận ñể có bk của (C) là r =4, d(I,(P)) =11/3 suy ra bbk của mặt cầu
R=
265
3
Pt mặt cầu :
( ) ( ) ( )
2 2 2
265
2 2 2
9
x y z− + − + + = ……………………..
• Gọi H là tâm của ñường tròn (C) thì H là hình chiếu của I trên mặt phẳng(P)
( )
( )
11
9
2 2 5 0 4
2 2
4 4 29
9
... ; ;
2 2 4
9 9 9
9
2
29
9
H P
IH P
t
x y z
x
x t H
y t y
z t
z
∈
⇔⊥
= −
+ + + =
= −
= +
⇔ ⇔ ⇔ ⇒− − −
= +
= −
= −
= −
uuur
0,25
0,25
0,25
0,25
Đ
Ề
S
Ố
027
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
112
http://www.VNMATH.com