Đềthi thử
tốt nghiệp
THPT
môn toán
2022
Sevendung Nguyen
Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIA LAI
ĐỀ THI THAM KHẢO
ĐỀ SỐ 01
KỲ
THI TỐT NGHIỆP TRUNG HỌC PHỔ
THÔNG NĂM 202
2
Bài thi: TOÁN
Thời gian làm bài: 90 phút ( không kể
thời gian phát đề)
Câu 1. Từ một nhóm học sinh gồm 20 nam và 25 nữ, có bao nhiêu cách chọn một nam và một nữ?
A. 45. B. 2
45
C. C. 2
45
A. D. 500 .
Câu 2. Cho cấp số cộng
n
u với 12u và công sai 3d. Số hạng thứ năm của cấp số cộng đã cho
bằng
A. 14. B. 10. C. 162. D. 30.
Câu 3. Cho hàm số
f x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;4 . B.
; 1 . C.
1;1. D.
0;2 .
Câu 4. Cho hàm số
f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại
A. 1x . B. 3x . C. 1x. D. 0x.
Câu 5. Cho hàm số
f x có bảng xét dấu của
f x
như sau:
Số điểm cực tiểu của hàm số đã cho là
A. 0. B. 2. C. 1. D. 3.
Câu 6. Tiệm cận ngang của đồ thị hàm số2 3
1
x
yx
là
A. 1y. B. 2y. C. 1x. D. 2x.
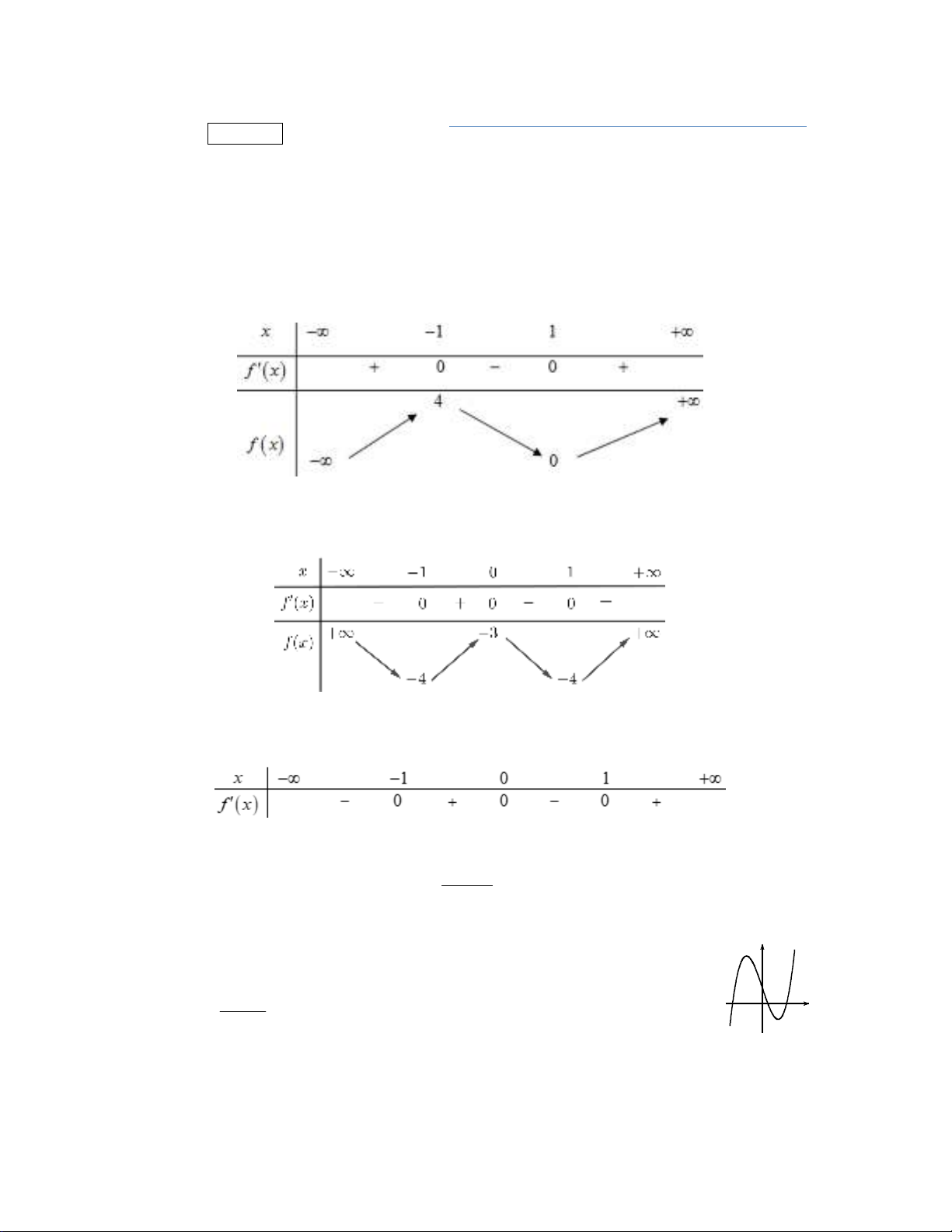
Câu 7. Hàm số nào dưới đây có đồ thị dạng như đường cong trong hình bên?
A. 33 1y x x. B. 4 2
2 1y x x .
C. 2 1
1
x
yx
. D. 33 1y x x .
Câu 8. Số giao điểm của đồ thị hàm số 3 2
5 3 5y x x x và đồ thị hàm số
2
2 5y x x là
A. 0. B. 1. C. 2. D. 3.
Câu 9. Với a là số thực dương khác 1 và b là số thực dương tùy ý,
2
logaa b bằng
x
y
O
Trang 2
A.
2 log
a
b
. B.
a
b
. C.
1 2 log
a
b
. D.
2log
a
b
.
Câu 10. Hàm số
1 2
x
y
có đạo hàm là
A.
1 2
2 .
x
y
B. 1 2
ln .
x
y
C. 1 2
2 ln .
x
y
D.
1 2
.
x
y
Câu 11. Với
a
là số thực dương tùy ý,
2
2
log 4
a
bằng
A.
2
2 log 2
a
. B.
2
1
log 2
2
a
. C.
2
2 log 2
a
. D. 2
1
log 2
2
a
.
Câu 12. Tập nghiệm của phương trình
2
0,25
log 3 1
x x
là
A.
4
. B.
1; 4
. C.
3 2 2 3 2 2
;
2 2
. D.
1; 4
.
Câu 13. Tập xác định của hàm số
2
log 1
y x
là
A.
;1
 . B.
1;
. C.
\ 1
. D.
.
Câu 14. Họ tất cả các nguyên hàm của hàm số
( ) 2 1
f x x
là
A. 2
x x C
. B. 2
1
x C
. C. 2
2
x x C
. D. 2
x C
.
Câu 15. Cho hàm số
sin 2
f x x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
1
dx cos 2
2
f x x C
. B.
1
dx cos 2
2
f x x C
.
C.
dx 2cos2
f x x C
. D.
dx 2cos2
f x x C
.
Câu 16. Nếu
2
0
d 3
f x x
và
2
0
d 1
g x x
thì
2
0
5 d
f x g x x x
bằng
A.
12
. B.
0
. C.
8
. D.
10
.
Câu 17. Xét
d
2
sin
0
cos . x
x e x
, nếu đặt
sin
u x
thì
d
2
sin
0
cos . x
x e x
bằng
A.
e d
u
1
0
2u
. B.
e d
u
1
0
u
. C.
e d
u
1
2
0
u
. D.
e d
u
2
0
u
.
Câu 18. Số phức liên hợp của số phức
2 3
z i
là
A.
2 3
z i
. B.
2 3
z i
. C.
2 3
z i
. D.
2 3
z i
.
Câu 19. Cho hai số phức
1
3 2
z i
và
2
1
z i
. Phần ảo của số phức
1 2
z z
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 20. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
1 2
z i
là điểm nào dưới đây?
A.
1; 2
Q. B.
1; 2
P. C.
1; 2
N
. D.
1; 2
M
.
Câu 21. Thể tích của khối lập phương cạnh
a
bằng
A.
3
3
a
. B.
3
a
. C.
3
4
a
. D.
3
6
a
.
Câu 22. Cho khối chóp có diện tích đáy
4
B
và chiều cao
6.
h
Thể tích của khối chóp đã cho bằng
A.
24
. B.
8
. C.
72
. D.
12
.
Câu 23. Cho khối nón có chiều cao
4
h
và bán kính đáy
3.
r
Thể tích của khối nón đã cho bằng
A.
12
. B.
36
. C.
16
. D.
4
.
Câu 24. Diện tích của mặt cầu có bán kính
R
bằng
Trang 3
A.
2
R
. B.
2
2
R
. C.
2
4
R
. D.
2
4
3
R
.
Câu 25. Trong không gian với hệ trục tọa độ
Oxyz
, cho
3 4 2 5
AO i j k j

. Tọa độ của điểm
A
là
A.
3; 2; 5
A
. B.
3; 17; 2
A
. C.
3;17; 2
A
. D.
3; 5; 2
A
.
Câu 26. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
: 6 4 8 4 0.
S x y z x y z
Tìm tọa độ
tâm
I
và tính bán kính
R
của
S
.
A.
3; 2; 4
I
,
25
R
. B.
3;2; 4
I
,
5
R
.
C.
3; 2; 4
I
,
5
R
. D.
3;2; 4
I
,
25
R
.
Câu 27. Trong không gian
,
Oxyz
cho mặt phẳng
: 2 2 0
x y z
. Điểm nào dưới đây thuộc
?
A.
1; 2;2
Q
. B.
1; 1; 1
N
. C.
2; 1; 1
P
. D.
1;1; 1
M
.
Câu 28. Trong không gian , mặt phẳng () đi qua (2; −1; 3), (0; 4; 1) và song song với trục 
có một vectơ pháp tuyến là
A.
( 2; 5; 2).
n
B.
(2; 0; 5).
n
C.
(5; 0; 2).
n
D.
(5;2; 0).
n
Câu 29. Chọn ngẫu nhiên một số trong 10 số nguyên dương đầu tiên. Xác suất để chọn được số nguyên tố
bằng
A.
3
10
. B.
2
5
. C.
1
2
. D.
1
5
.
Câu 30. Hàm số nào dưới đây nghịch biến trên khoảng
1; 5
?
A.
2 1
2
x
x
. B.
3
4
x
x
. C.
3 1
1
x
y
x
. D.
1
3 2
x
y
x
.
Câu 31. Giá trị lớn nhất của hàm số 4 2
( ) 4 1
f x x x
trên đoạn
1 ; 3
bằng
A.
46
. B.
64
. C.
3
. D.
2
.
Câu 32. Tập nghiệm của bất phương trình 1
32
2
x
là
A.
;5
. B.
; 5
. C.
5;
. D.
5;
.
Câu 33. Nếu
2
0
d 3
f x x
và
2
0
d 1
g x x
thì
2
0
5 d
f x g x x x
bằng
A.
12
. B.
0
. C.
8
. D.
10
.
Câu 34. Cho hai số phức
1
2
z i
và
2
3
z i
. Phần ảo của số phức
1 2
z z
bằng
A.
5
. B.
5
i
. C.
5
. D.
5
i
.
Câu 35. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
có
, 2
AB a AA a
. Góc giữa đường thẳng
A C
với mặt phẳng
AA B B
bằng:
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 36. Cho hình chóp
.
S ABCD
có đáy là hình thoi tâm
O
, tam giác
ABD
đều có cạnh bằng
2,
a
SA
vuông góc với mặt phẳng đáy và
3 2
2
a
SA (minh họa như hình bên). Góc giữa đường thẳng
SO
và mặt
phẳng
ABCD
bằng
Trang 4
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 37. Trong không gian
,
Oxyz
cho ba điểm
2; 2; 2 ,
A
2; 2;0
B và
4;1; 1 .
C Điểm nào dưới đây
thuộc mặt phẳng
Ozx
và cách đều
A
,
B
,
C
?
A.
3 1
; 0;
4 2
M
. B.
3 1
; 0;
4 2
N
. C.
3 1
; 0;
4 2
P
. D.
3 1
; 0;
4 2
Q
.
Câu 38. Trong không gian
Oxyz
, cho hình bình hành
ABCD
có
0;1; 2 , 3; 2;1
A B
và
1; 5; 1
C
. Phương trình tham số của đường thẳng
CD
là:
A.
1
5
1
x t
y t
z t
B.
1
5
1
x t
y t
z t
C.
1 3
5 3
1 3
x t
y t
z t
D.
1
5
1
x t
y t
z t
Câu 39. Cho hàm số
y f x
có đồ thị
f x
như hình vẽ
Giá trị nhỏ nhất của hàm số
3
1
3
g x f x x x
trên đoạn
1;2
bằng
A.
2
2
3
f
. B.
2
1
3
f
. C.
2
3
. D.
2
1
3
f
.
Câu 40. Giả sử
0 0
;
x y
là cặp nghiệm nguyên không âm có tổng
0 0
S x y
lớn nhất của bất phương
trình
4 2 .3 9.2 3 10
x x y x y
, giá trị của
S
bằng
A.
2
. B.
4
. C
3
. D.
5
.
Câu 41. Cho hàm số
2
2
0
( )
e
0
2
xkhi x
x
f x khi xx
. Biết tích phân
1
2
1
e
( )d a
f x x
b c
(
a
b
là phân
số tối giản). Giá trị
a b c
bằng
A.
7
. B.
8
. C.
9
. D.
10
.
Câu 42. Tìm số phức
z
thỏa mãn 2
z z
và
1
z z i
là số thực.
A.
1 2 .
z i
B.
1 2 .
z i
C.
2 .
z i
D.
1 2 .
z i
O
D
A
C
B
S