TRƯỜNG THPT LƯƠNG THẾ VINH
Đề thi có 7 trang
Mã đề thi 111
ĐỀTHI THỬ LẦN 1 - NĂM HỌC 2019-2020
Môn: Toán lớp 12
Thời gian làm bài:90 phút (50 câu trắc nghiệm)
Học sinh tô đáp án đúng nhất vào Phiếu trả lời trắc nghiệm
Câu 1. Cho hàm số y=f(x)có bảng biến thiên như sau.
x
f′(x)
f(x)
−∞ 0 3 +∞
+0−0+
−∞−∞
44
−1−1
+∞+∞
Mệnh đề nào sau đây đúng?
A. Hàm số có điểm cực tiểu x=−1B. Hàm số có điểm cực tiểu x=3
C. Hàm số có điểm cực tiểu x=0D. Hàm số có điểm cực đại x=4
Câu 2. Đường cong trong hình vẽ bên là của hàm số nào trong 4 hàm số dưới đây?
A. y=−x4+2x2−1B. y=−x3+3x2−1
C. y=x4−x2−4D. y=x4−2x2−1O
x
y
2
−1
−√3√3
Câu 3.
Cho đồ thị của hàm số y=f(x)như hình vẽ. Tìm số giá trị nguyên của mđể
phương trình f(x)=mcó đúng 3nghiệm phân biệt.
A. 0
B. 3
C. 1
D. 2
x
y
O
−2−1 1 2 3
1
2
3
4
−1
Câu 4.
Cho hàm số y=f(x)liên tục trên đoạn [−1; 3] có đồ thị như hình vẽ bên. Gọi
Mvà mlần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn
[−1; 3]. Giá trị của M−mbằng
A. 0B. 1C. 4D. 5x
y
−1
2
3
3
2
1
−2
O
Trang 1/7 Mã đề 111

Câu 5. Cho khối trụ (T)có bán kính đáy bằng 4và diện tích xung quanh bằng 16π. Tính thể tích Vcủa khối
trụ (T).
A. V=16πB. V=64πC. V=32π
3D. V=32π
Câu 6. Giá trị của biểu thức M=log22+log24+log28+. . . +log2256 bằng
A. 56 B. 8 log2256 C. 36 D. 48
Câu 7. Tiệm cận ngang của đồ thị hàm số y=3x+2
x+1là
A. x=−1B. x=3C. y=3D. y=−1
Câu 8. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; 1; −2)và B(2; 2; 1). Véc tơ −−→
AB có tọa độ
là A. (3; 1; 1)B. (1; 1; 3)C. (3; 3; −1)D. (−1; −1; −3)
Câu 9. Trong không gian với hệ trục tọa độ Oxyz, cho véc tơ −→
a=(1; −2; 3). Tìm tọa độ của véc tơ −→
bbiết
rằng véc tơ −→
bngược hướng với véc tơ −→
avà −→
b
=2−→
a.
A. −→
b=(−2; −2; 3)B. −→
b=(−2; 4; −6)C. −→
b=(2; −2; 3)D. −→
b=(2; −4; 6)
Câu 10. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(1; 2; −4)và M′(5; 4; 2). Biết rằng M′là
hình chiếu vuông góc của Mlên mặt phẳng (α), khi đó mặt phẳng (α)có một véc tơ pháp tuyến là
A. −→
n=(2; −1; 3)B. −→
n=(3; 3; −1)C. −→
n=(2; 1; 3)D. −→
n=(2; 3; 3)
Câu 11. Cho biểu thức P=
3
rx4
qx3√x, với x>0. Mệnh đề nào dưới đây đúng?
A. P=x1
2B. P=x7
24 C. P=x5
8D. P=x7
12
Câu 12. Hàm số y=x3−3x+5đồng biến trên khoảng nào dưới đây?
A. (−1; +∞)B. (−∞;−1)∪(1; +∞)C. (−∞;−1)và (1; +∞)D. (−∞; 1)
Câu 13. Tích phân
e
Z
1
1
xdxcó giá trị bằng
A. 1B. 1−eC. e−1D. 2
Câu 14. Cho khối chóp S.ABC có diện tích đáy bằng 2a2, đường cao S H =3a. Thể tích của khối chóp S.ABC
là
A. 3a3
2B. a3C. 2a3D. 3a3
Câu 15. Trong các khẳng định sau, khẳng định nào sai?
A. Z2xdx=2xln 2 +CB. Zcos 2xdx=1
2sin 2x+C
C. Ze2xdx=e2x
2+CD. Z1
x+1dx=ln |x+1|+C (∀x,−1)
Câu 16. Tập hợp nào sau đây không thuộc tập hợp nghiệm của bất phương trình 4x<2x+1+3?
A. (−∞; log23) B. (−∞; 1) C. (1; log23) D. (1; 3)
Câu 17. Cho khối chóp S.ABC có S A,S B,S C đôi một vuông góc với nhau và S A =a,S B =2a,S C =3a.
Thể tích của khối chóp S.ABC là
A. a3
3B. 2a3C. a3D. a3
6
Câu 18. Phương trình log3(5x+2)=3có nghiệm là
A. x=5B. x=25
3C. x=29
5D. x=7
5
Câu 19. Tìm tập xác định Dcủa hàm số y=(x2−3x)−2020.
A. D=(−∞; 0] ∪[3; +∞)B. D=R\ {0; 3}
C. D=(−∞; 0) ∪(3; +∞)D. D=(0; 3)
Trang 2/7 Mã đề 111
Câu 20. Cho
1
Z
0
f(x) dx=2và
1
Z
0
g(x) dx=1, khi đó
1
Z
0f(x)−2g(x)dxbằng
A. 4B. 3C. 0D. 1
Câu 21.
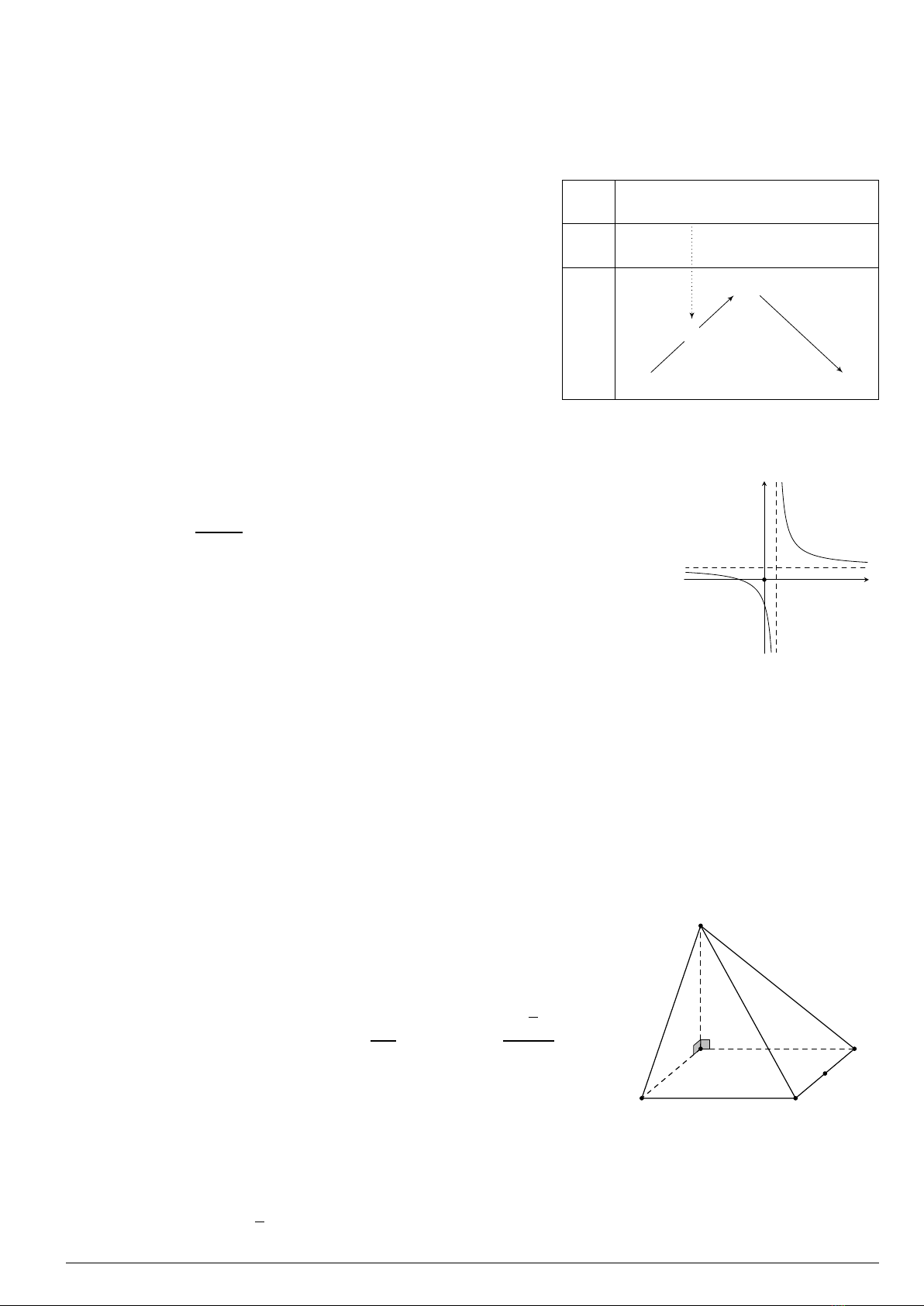
Cho hàm số y=f(x)có bảng biến thiên như hình vẽ. Xét các mệnh
đề
1. Hàm số đồng biến trên khoảng (−3; −2).
2. Hàm số đồng biến trên khoảng (−∞; 5).
3. Hàm số nghịch biến trên khoảng (5; +∞).
4. Hàm số đồng biến trên khoảng (−∞;−2).
x
f′(x)
f(x)
−∞ 2+∞
+0+0−
−∞−∞
55
−∞−∞
−3
0
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 3B. 4C. 1D. 2
Câu 22.
Cho hàm số y=ax +b
cx +d(d<0) có đồ thị như hình bên. Khẳng định nào dưới đây
là đúng?
A. a<0,b>0,c<0B. a>0,b>0,c>0
C. a>0,b>0,c<0D. a>0,b<0,c>0
x
y
O
Câu 23. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): x2+y2+z2−4x−2y+4z=0và mặt
phẳng (P): x+2y−2z+1=0. Gọi (Q)là mặt phẳng song song với mặt phẳng (P)và tiếp xúc với mặt cầu
(S). Phương trình của mặt phẳng (Q)là
A. (Q): x+2y−2z−35 =0B. (Q) : x+2y−2z−17 =0
C. (Q): x+2y−2z+1=0D. (Q) : 2x+2y−z+19 =0
Câu 24. Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(−3; 2; 4). Gọi A,B,Clà hình chiếu của M
trên trục Ox,Oy,Oz. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (ABC).
A. 4x−6y−3z+12 =0B. 3x−6y−4z+12 =0
C. 4x−6y−3z−12 =0D. 6x−4y−3z−12 =0
Câu 25.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a,S A vuông
góc với mặt phẳng (ABCD)và S A =2a. Gọi Mlà trung điểm của cạnh
BC. Thể tích khối chóp S.ADCM là
A. 6a3B. 2a3C. 8a3
3D. 4√2a3
3
S
D
B
C
M
A
Câu 26. Trong không gian với hệ trục tọa độ Oxyz, cho A(1; 2; 5),B(3; 4; 1),C(2; 3; −3),Glà trọng tâm của
tam giác ABC và Mlà điểm thay đổi trên mp (Oxz). Độ dài GM ngắn nhất bằng
A. 4B. 3C. 2D. 1
Câu 27. Cho hàm số y=f(x)có đạo hàm liên tục trên Rthỏa mãn f′(x)−x·f(x)=0,f(x)>0,∀x∈Rvà
f(0) =1. Giá trị của f(√2) bằng
Trang 3/7 Mã đề 111
A. eB. 1
eC. e2D. √e
Câu 28. Tìm tổng các nghiệm của phương trình log3|x+2|=2.
A. S=6B. −4C. S=−10 D. S=4
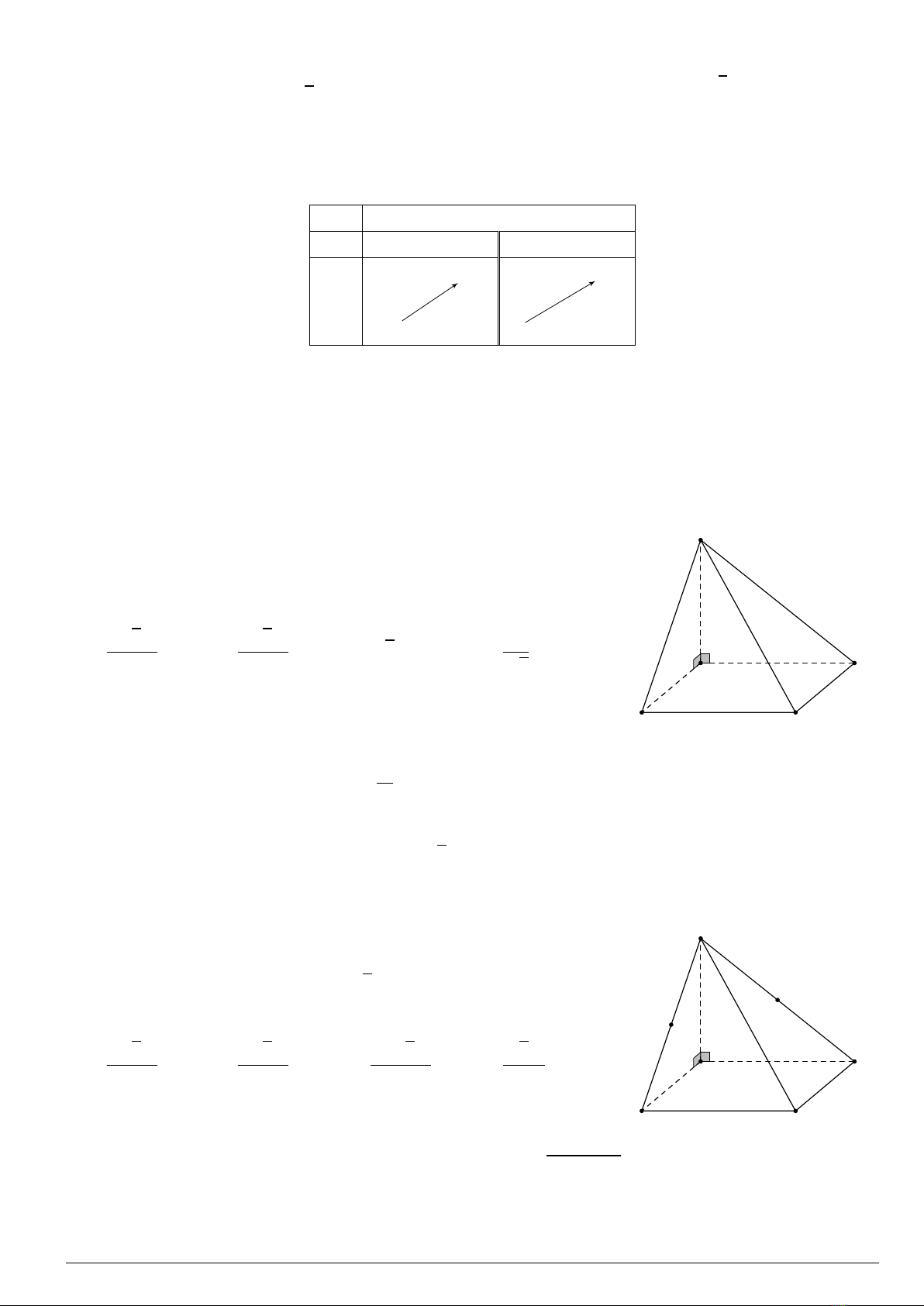
Câu 29. Cho hàm số y=f(x)có bảng biến thiên như sau.
x
y′
y
−∞ 1+∞
++
22
+∞
3
66
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4B. 3C. 1D. 2
Câu 30. Cho hàm số y=f(x)xác định liên tục trên Rvà f′(−2) =3. Tiếp tuyến của đồ thị hàm số y=f(x)
tại tiếp điểm có hoành độ x=−2là đường thẳng y=3x+4. Đặt g(x)=f(x)2, khi đó giá trị của g′(−2) là
A. −4B. −12 C. 12 D. 6
Câu 31.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2avà S A vuông
góc với đáy. Biết khoảng cách giữa AC và S B bằng a. Tính thể tích khối
chóp S.ABCD.
A. 2√2a3
3B. 4√2a3
3C. √2a3D. 3a3
√2
S
D
B
C
A
Câu 32. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hai hàm số y=2xvà y=1
2xđối xứng nhau qua trục hoành
B. Đồ thị của hai hàm số y=2xvà y=log2xđối xứng nhau qua đường thẳng y=−x
C. Đồ thị của hai hàm số y=log2xvà y=log2
1
xđối xứng nhau qua trục tung
D. Đồ thị của hai hàm số y=2xvà y=log2xđối xứng nhau qua đường thẳng y=x
Câu 33.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,S A vuông
góc với mặt phẳng (ABCD)và S A =a√3. Gọi M,Nlần lượt là trung điểm
của cạnh S B và S D; mặt phẳng (AMN)cắt S C tại I. Tính thể tích khối đa
diện ABCDMNI.
A. 5√3a3
18 B. 5√3a3
6C. 13 √3a3
36 D. √3a3
18
S
D
N
B
C
M
A
Câu 34. Cho hàm số f(x)xác định trên R\ {−2; 1}có f′(x)=2x+1
x2+x−2thỏa mãn f(0) =1. Giá trị f(−1)
bằng
A. 3B. 1+2 ln 2 C. 1−2 ln 2 D. 1
Trang 4/7 Mã đề 111
Câu 35. Số giá trị nguyên của mđể phương trình 4x−m·2x+1+4m=0có hai nghiệm phân biệt x1,x2và
x1+x2=3là
A. 1B. 2C. 3D. 0
Câu 36. Có tất cả bao nhiêu giá trị nguyên của tham số mthuộc [−10; 10]để đồ thị hàm số y=
√mx2−4
x−1có
ba đường tiệm cận?
A. 7B. 8C. 10 D. 6
Câu 37. Tìm số các giá trị nguyên không dương của tham số mđể hàm số y=mln x−2
ln x+m−3đồng biến trên
(e2;+∞)là
A. 2B. vô số C. 0D. 1
Câu 38. Biết Zf(x) dx=2xe2x+1+C. Tìm khẳng định đúng trong các khẳng định sau.
A. Zf(2x) dx=2xe2x+1+CB. Zf(2x) dx=2xe4x+1+C
C. Zf(2x) dx=4xe4x+1+CD. Zf(2x) dx=xe4x+1+C
Câu 39. Số các giá trị nguyên của mthuộc [−2020; 2020]để bất phương trình log5(x)≥log5mđúng với
∀x∈[5; 25]là
A. S=2022 B. S=3C. 5D. S=2
Câu 40. Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(3; −2; −2)và mặt phẳng (P): x−y−z+1=0.
Mặt phẳng (Q): ax +by +cz +d=0đi qua A, vuông góc với mặt phẳng (P)và (Q)cắt hai tia Oy,Oz lần lượt
tại hai điểm phân biệt M,Nsao cho OM =ON (Olà gốc tọa độ). Tìm d
a.
A. 3B. 2C. 1D. −1
Câu 41. Tìm số giá trị của tham số mđể
m
Z
0
(2x+1)dx=2.
A. 0B. 1C. 3D. 2
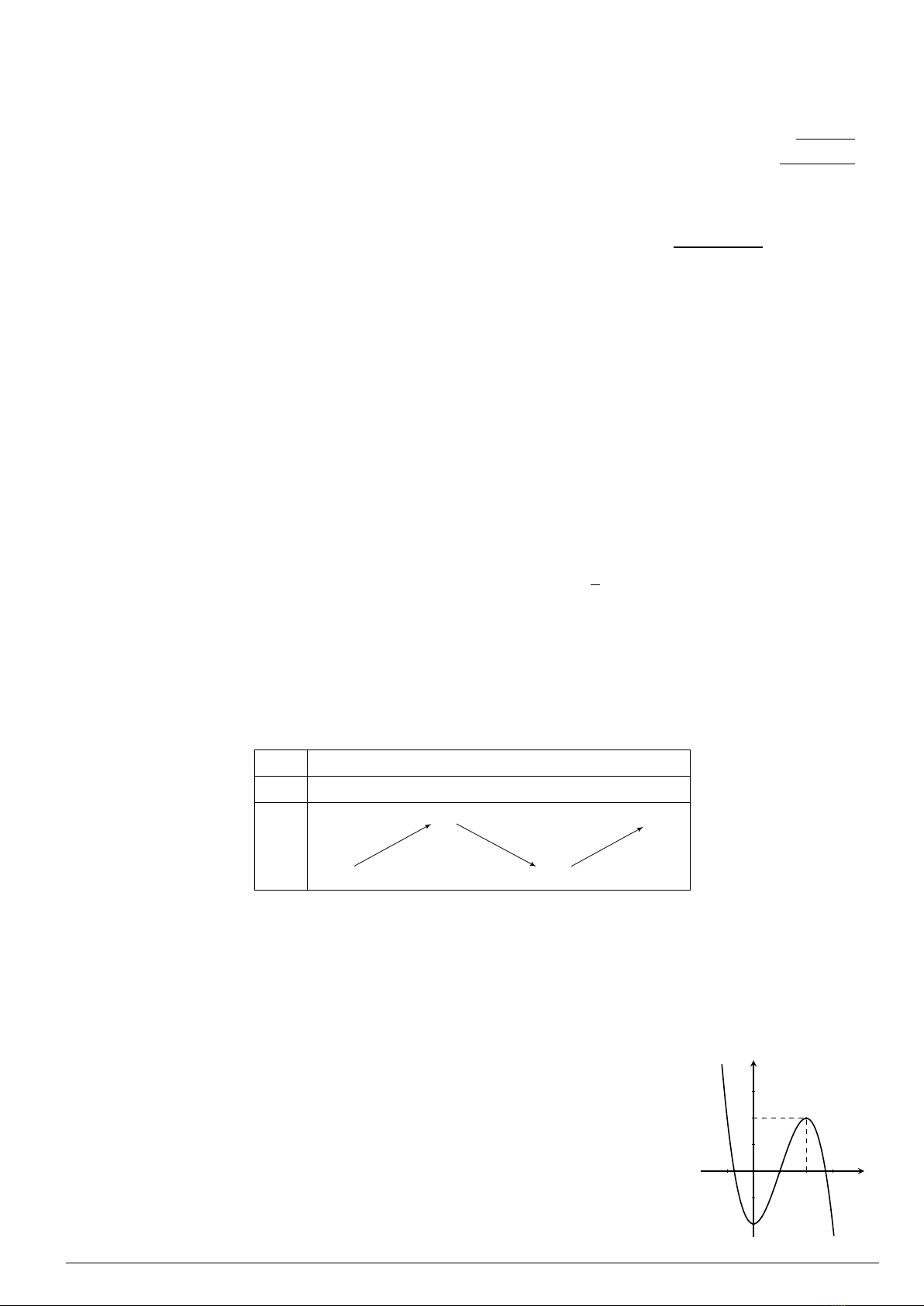
Câu 42. Cho hàm số y=f(x)có bảng biến thiên
x
f′(x)
f(x)
−∞ 13+∞
+0−0+
−∞−∞
33
−2−2
+∞+∞
Tìm tất cả các giá trị của mđể bất phương trình f3−x2≤mvô nghiệm?
A. m≥3B. m>−2C. m≤3D. m>3
Câu 43. Có bao nhiêu cặp số nguyên (a;b)thỏa mãn 1<a<b<100 để phương trình abx
=baxcó nghiệm
nhỏ hơn 1?
A. 4751 B. 4656 C. 2D. 4750
Câu 44.
Cho hàm số y=f(x)có đạo hàm trên R. Biết rằng hàm số y=f(x)có đồ thị như
hình bên. Đặt g(x)=f(f(x)). Hỏi hàm số g(x)có bao nhiêu điểm cực trị?
A. 4B. 5C. 7D. 6x
y
O
−1 1 2 3
−2
−1
1
2
3
Trang 5/7 Mã đề 111




















![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)





