1
-------------------------------------------
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7 điểm)
Câu 1 (3 điểm)
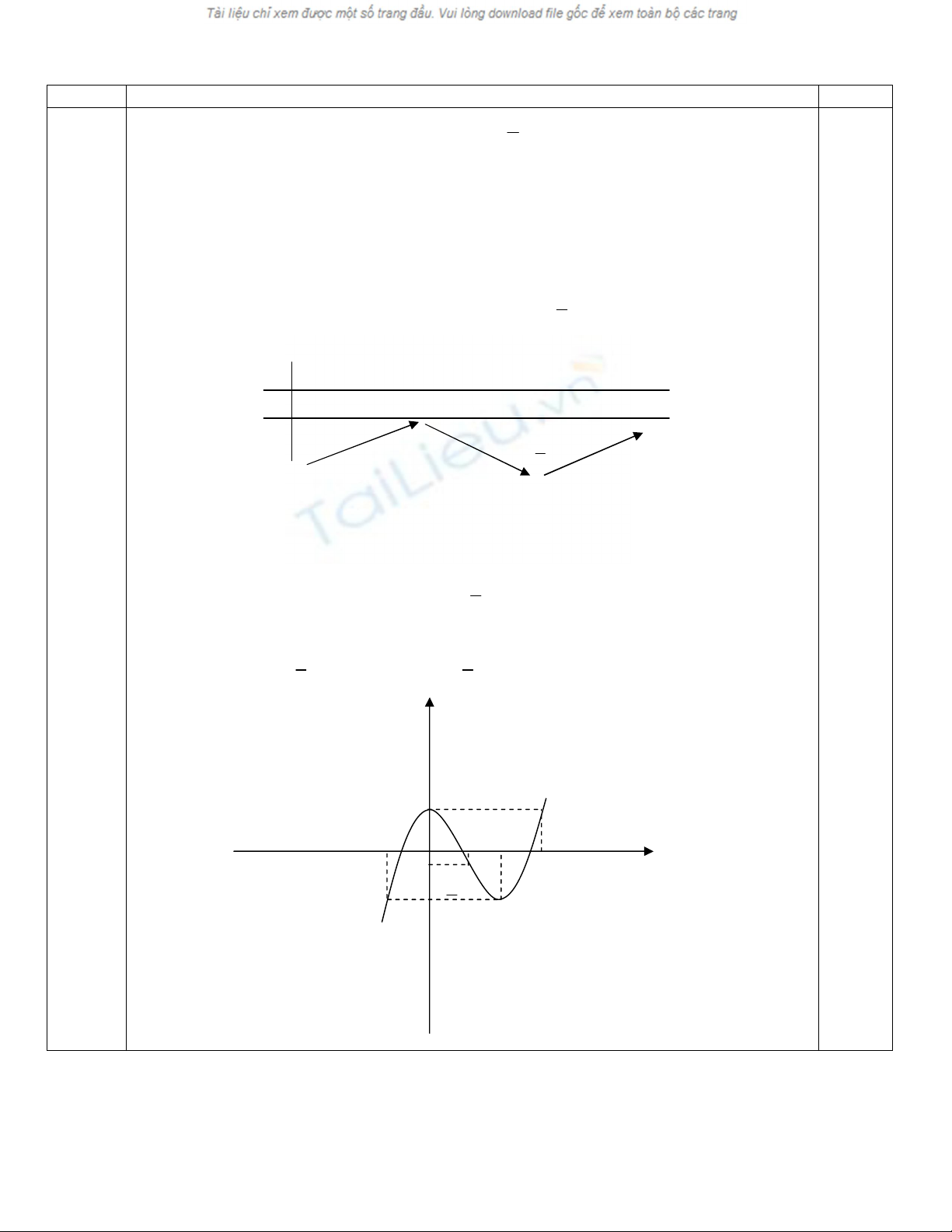
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số
3 2
2
2 1 C
3
y x x (2 điểm)
2. Dựa vào đồ thị
C
, tìm
m
để phương trình: 3 2
2
3
x x m
có 3 nghiệm phân biệt? (1 điểm)
Câu 2 (3 điểm)
1. Giải phương trình: 2
9 3
4log log 6 0
x x
(1 điểm)
2. Tính tích phân
1
e
I dx
(1 điểm)
3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2 2x - ln x
.y x e, với 1
; e
xe
(1 điểm)
Câu 3 (1 điểm)
Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
. Biết
SA ABCD
, góc tạo bởi
cạnh bên
SB
và mặt phẳng
D
ABC
bằng
0
60
. Tính thể tích khối chóp .
S OBC
theo
a
? (1 điểm)
II. PHẦN RIÊNG( 3 điểm) Thí sinh chọn 1 trong 2 phần ( phần A hoặc phần B )
A. Theo chương trình chuẩn:
Câu 4a. (2 điểm) Trong không gian
Oxyz
, cho mặt phẳng
: 2x + y - 2z - 8= 0
P
1. Lập phương trình mặt phẳng
Q
đi qua điểm
1;2;3
M và song song với mặt phẳng
P
. (1 điểm)
2. Lập phương trình mặt cầu
S
có tâm là trung điểm của đoạn thẳng
AB
, với
4,6, 8 ; 2;2;9
A B
và tiếp xúc với mặt phẳng
P
? (1 điểm)
Câu 5a. (1 điểm) Tìm môđun của số phức
2
z z
, biết
4 2
z i
. (1 điểm)
B. Theo chương trình nâng cao:
Câu 4b. (2 điểm)
Trong không gian
Oxyz
, cho các điểm
2; 3; 1
A
,
2;1;6 , 3; 0; 1 , D(-1;-2;0)
B C
1. Chứng tỏ
, , ,
A B C D
là 4 đỉnh một tứ diện. Tính độ dài đường cao
DH
của tứ diện
ABCD
, điểm
H
thuộc mặt phẳng
ABC
. (1 điểm)
2. Lập phương trình mặt cầu có tâm
A
, tiếp xúc cạnh
CD
. Tìm tọa độ tiếp điểm? (1 điểm)
Câu 5b. (1 điểm) Gi¶i bÊt ph¬ng tr×nh:
3x
3x 2
2 2 6
. (1 điểm)
------------------------------------------------Hết----------------------------------------------------
(Cán bộ coi thi không giải thích gì thêm)
Trường T.H.P.T Lê Thành Phương
Tổ Toán
ĐỀ THI THỬ TỐT NGHIỆP - MÔN TOÁN LỚP 12
Năm học: 2012 – 2013
Thời gian 150 phút, không kể thời gian phát đề
2
CÂU ĐÁP ÁN ĐỀ THI THỬ TỐT NGHIỆP MÔN TOÁN - LỚP 12 NĂM HỌC 2012-2013 ĐIỂM
Câu 1 1/ Khảo sát sự biến thiên và vẽ đồ thị hàm số
3 2
2
2 1 C
3
y x x
TXĐ
D R
lim ; lim
x x
y y
 
 
2 2
0
' 2 4 ; ' 0 2 4 0
2
x
y x x y x x x
1
5
3
y
y
Bảng biến thiên
Hàm số đồng biến trong
;0
 và
2;

Hàm số nghịch biến trong
0;2
Điểm cực đại
1
0;1
I, điểm cực tiểu 2
5
2;
3
I
Đồ thị
Điểm đặc biệt
1
1;
3
A
,
3;1
B,
5
1;
3
C
0.25
0.25
0.25
0.5
0.25
0.5
2
x


5
3
y
'
y
0
0 0
-
+ +


1
3 2
1 -1
1
0
-1
5
3
.
. . .
.
.
y
x
A
B
C
1
I
2
I
3
2/ Phương trình tương đương
3 2
2
2 1 = *
3
x x m
*
là phương trình hoành độ giao điểm của đồ thị
3 2
2
2 1 C
3
y x x và đường
thẳng
d y m
song song trục
Ox
. Số nghiệm của phương trình đã cho chính bằng số
giao điểm của
C
và
d
+ Để phương trình đã hco có 3 nghiệm phân biệt thì 5 5
1 1
3 3
y m
Vậy 5
; 1
3
m
thì phương trình đã cho có 3 nghiệm phân biệt.
0.25
0.25
0.25
0.25
1. Phương trình 2
9 3
4log log 6 0
x x
Điều kiện
0
x
Phương trình tương đương
2
22
3 3 3
3
4 log log 6 0 log log 6 0
x x x x
3
3
27
log 3
1
log 2
9
x
x
xx
0.25
0.25
0.5
2. Tích phân
1
2x-2 ln x
e
I dx
Đặt
2
1
ln x
x
dv= 2x-2 x
v=x 2x
u
du d
x
d
Suy ra
e
2 2
11
1
2x ln x 2x . x
e
I x x d
x
2
3
2 2
e
0.5
0.25
0.25
Câu 2
3.
2 2x
2
lnx
.
.
e
x
x e
y x e
, 1
; e
xe
.
Ta có
' 2 1 .
x
y x e
1
' 0, ;
y x e
e
. Suy ra hàm số tăng trên 1
; e
e
Vậy giá trị lớn nhất của hàm số là
2e+1
1;x e
e
max f x f e e
,
giá trị nhỏ nhất của hàm số là
2
1
1;
1
e
x e
e
min f x f e
e
.
0.25
0.25
0.25
0.25