Trường THCS Hồng Hà ĐỀ THI THỬ VÀO LỚP 10
Năm học 2021 – 2022
Môn thi: Toán 9
Thời gian làm bài:120 phút
Bài I.(2,0 điểm)
Cho hai biểu thức A = và B = với x 0, x 4.
1) Tính giá trị của biểu thức A khi x = 9.
2) Rút gọn B.
3) Tìm tất cả các giá trị của x để nhận giá trị là một số nguyên.
Bài II.(2,5 điểm)
1.Một phòng họp có 360 ghế ngồi được sắp xếp thành từng hàng, mỗi hàng có số
ghế như nhau. Vì có 418 người đến dự họp, do đó ban tổ chức chẳng những phải kê thêm
hai hàng ghế và mỗi hàng ghế phải xếp nhiều hơn quy định 1 ghế mới đủ chỗ ngồi. Hỏi lúc
đầu phòng họp có bao nhiêu hàng ghế và mỗi hàng ghế có bao nhiêu ghế? Biết số hàng
ghế không vượt quá 25.
2. Một hình cầu có thể tích . Tính diện tích mặt cầu đó.
Bài III.(2,0 điểm)
1.Giải hệ phương trình
2. a) Cho phương trình: (với m là tham số). Tìm m để phương trình có hai nghiệm phân
biệt?
b) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): và parabol (P): (với m là tham
số).
Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ là các số nguyên tố.
Bài IV. (3 điểm) Cho đường tròn (O) và đường thẳng d không đi qua tâm (O) cắt đường
tròn tại hai điểm A và B. Gọi C là điểm thuộc đường thẳng d sao cho A nằm giữa B và C.
Vẽ đường kính PQ vuông góc với dây AB tại D (P thuộc cung lớn AB). Tia CP cắt đường
tròn (O) tại điểm thứ hai là I (I khác P), AB cắt IQ tại K.
1) Chứng minh tứ giác PDKI nội tiếp.
2) Chứng minh KB.IQ = BQ.BI
3) Chứng minh IK là đường phân giác trong của AIB và .
4) Cho ba điểm A, B, C cố định còn đường tròn (O) thay đổi nhưng luôn đi qua AB.
Chứng minh đường thẳng IQ luôn đi qua một điểm cố định.
Bài V. (0,5 điểm) Cho x, y là các số không âm thoả mãn
Tìm giá trị lớn nhất của biểu thức
……………..Hết………….
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài ý Nội dung Điểm
I 2,0
1) Với x = 9 (thoả mãn 0,25
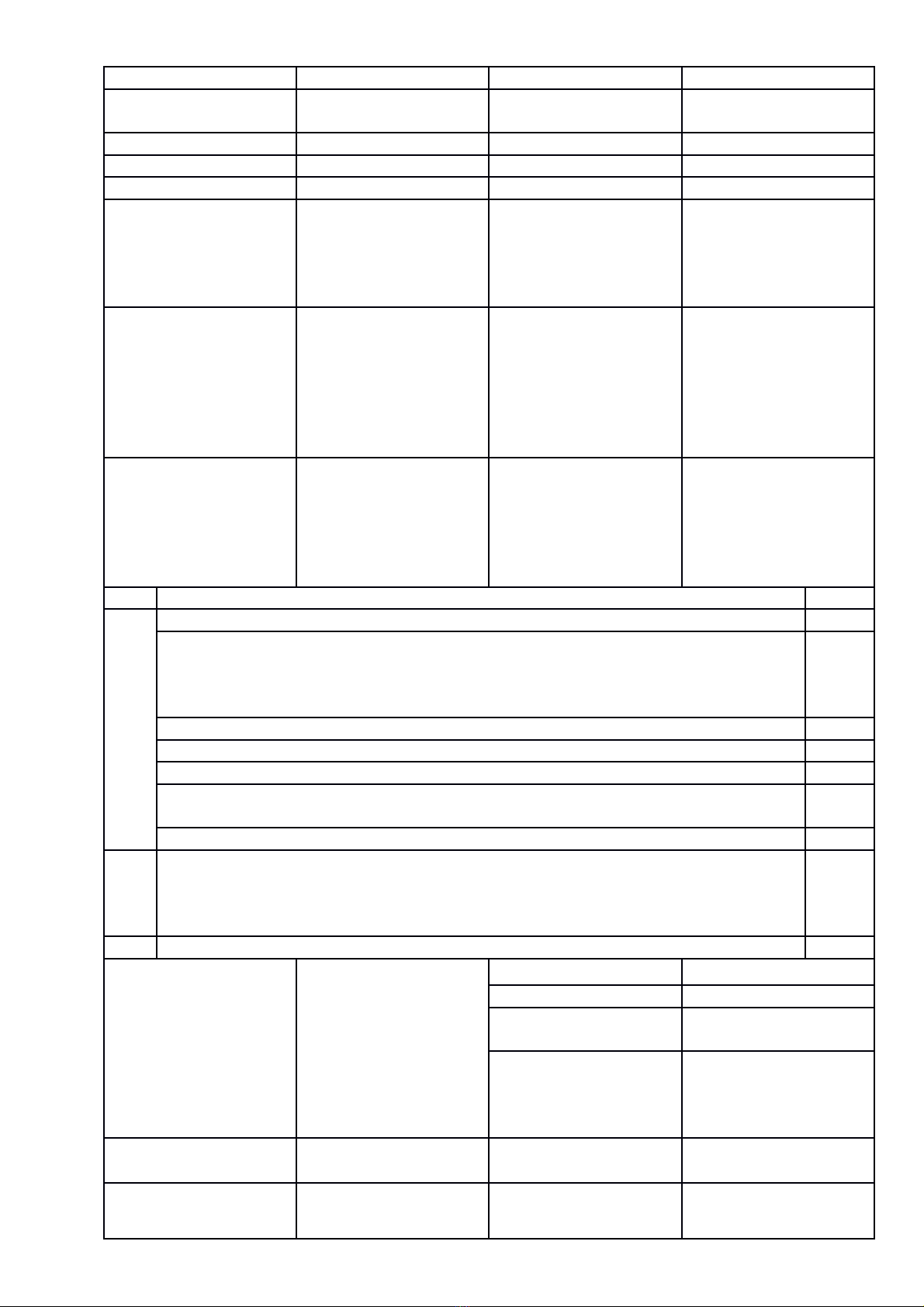
điều kiện)
Thay vào A ta được: A
= = 12
0,25
2) B = 0,25
= 0,25
= 0,25
=
0,25
3) .
Với x = 0 thì (thoả
mãn)
Vì x > 0 nên .
Mặt khác theo bất đẳng
thức Cô-si ta có:
Do đó
0,25
Với thì x + 3 = 4= 0
(thoả mãn điều kiện)
Vậy x = 0; x = 1; x = 9
là những giá trị để
nhận giá trị là một số
nguyên.
0,25
II 2,5
1.Gọi số hàng ghế lúc đầu của phòng họp là x (hàng) (x,) 0,25
Số hàng ghế sau khi kê thêm là: x + 2 (hàng).
Số ghế mỗi hàng ban đầu là: (ghế).
Số ghế mỗi hàng lúc sau là: (ghế) 0,25
Theo đề bài ta có phương trình: . 0,25
Phương trình trên tương đương với x2 – 56x + 720 = 0 0,5
Giải phương trình này ta được hai nghiệm là x = 20; x = 36 0,25
Kết hợp với điều kiện xta được x = 20. 0,25
Vậy ban đầu phòng họp đó có 20 hàng ghế, mỗi hàng có 360:20 = 18 ghế. 0,25
2. Ta có: Thể tích hình cầu là:
Diện tích mặt cầu đó là:
0,25
0,25
III 2,0
1) 1. ĐKXĐ: 0,25
Đặt 0,25
Giải được nghiệm hệ
mới là (4;1)
0,25
Giải được nghiệm hệ
ban đầu là (3; 3) và (-5;
3).
Kết luận
0,25
2a) Pt có 2 nghiệm phân
biệt
0,25
Tìm được: và kết
luận đúng
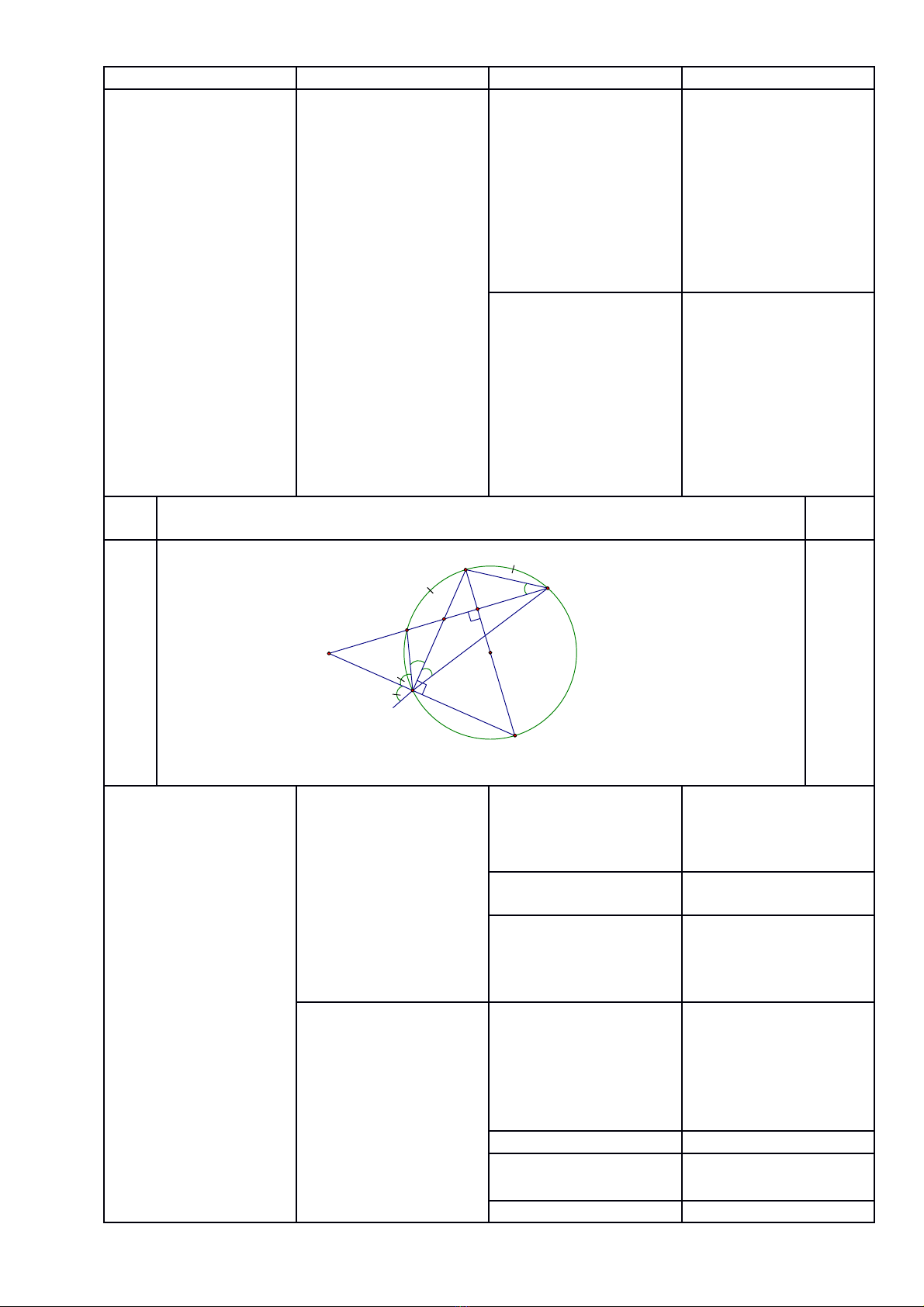
0,25
2b) Tính và lập
luận được để
PT có hai
nghiệm phân
biệt
0,25
Viết hệ thức Vi-
et
Lập luận được: Do các
nghiệm là các số
nguyên tố nên Kết
luận
0,25
IV 3,0
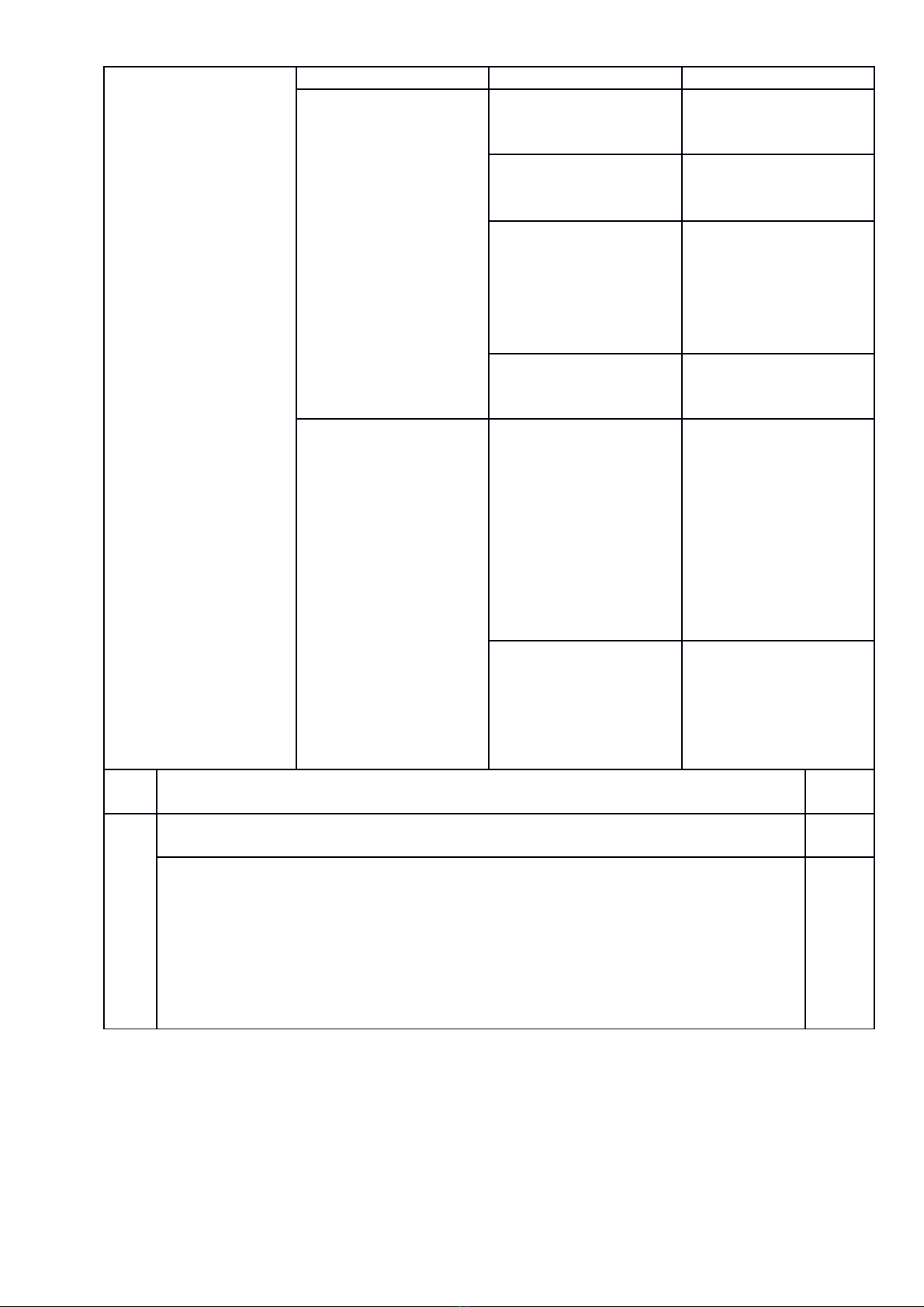
Vẽ hình đến câu a
D
K
I
P
Q
A
O
C
B
0,25
1Vì I thuộc đường tròn
đường kính PQ nên =
90o (góc nội tiếp chắn
nửa đường tròn).
0,25
Vì PQ vuông góc với
AB (gt) nên
0,25
Từ đó suy ra Tứ giác
PDKI nội tiếp (dấu
hiệu nhận biết tứ giác
nội tiếp).
0,25
2Vì PQ vuông góc với
AB nên Q là điểm
chính giữa cung AB
nên
(quan hệ giữa đường
kính và dây)
(tính chất góc nội tiếp) 0,25
KBQ đồng dạng với
BIQ (g – g)
0,25
(điều phải chứng 0,25
minh)
3Ta có (chứng minh
trên) nên (tính chất
góc nội tiếp).
Từ đó suy ra IK là
đường phân giác trong
của AIB (1)
0,25
Vì IC vuông góc với
IK (giả thiết) mà IK là
phân giác trong góc I
của AIB nên IC là
phân giác ngoài của
AIB
0,25
(2)
Từ (1) và (2) (điều
phải chứng minh) 0,25
4Vì tứ giác ABPI nội
tiếp, chứng minh được
CIA đồng dạng
CBP (g-g) CI.CP =
CA.CB (1)
Tương tự: Vì tứ giác
IKDP nội tiếp, chứng
minh được CIK đồng
dạng CDP (g-g)
CI.CP = CK.CD (2)
0,25
Từ (1) và (2) suy ra
CA.CB = CK. CD CK
= (không đổi vì C, A,
B, D cố định; D là
trung điểm của AB) K
là điểm cố định
0,25
V 0,5
Ta có: 0,25
0,25