TR NG THPT TH CH THÀNH ƯỜ Ạ
I
Đ THI MÔN TOÁN_ KH I 10 (l nỀ Ố ầ
2)
Năm h c: 2021 – 2022ọ
Th i gian: 120 phútờ
Câu 1 (1,0 đi m=0,5+0,5):ể
a) Hãy phát bi u m nh đ ph đnh c a m nh đ sau:ể ệ ề ủ ị ủ ệ ề
P
: “Có m t h c sinh c a l p không thích h c môn Toán”ộ ọ ủ ớ ọ
b) Cho các t p h p ậ ợ
{ } { }
1;2;3 , 2;3;4;5A B= =
. Xác đnh các t p h p sau: ị ậ ợ
,A B A B� �
.
Câu 2 (1,0 đi m=0,5+0,5):ể Gi i các ph ng trình sau:ả ươ
a)
2
9
1 1
x
x x
=
+ +
; b)
3 2 3 2x x+ = −
.
Câu 3 (1,0 đi m):ể Tìm
, ,abc
bi t parabol ế
2
y ax bx c= + +
có đnh ỉ
và c t tr c ắ ụ
tung t i đi m có tung đ b ng 6.ạ ể ộ ằ
Câu 4 (1,0 đi m=0,5+0,5):ể a) Cho hình bình hành
ABCD
và m t đi m ộ ể
M
tùy ý.
Ch ng minh r ng: ứ ằ
MB MA DM MC− = +
uuur uuur uuuur uuuur
.
b) Trong m t ph ng h t a đ ặ ẳ ệ ọ ộ
Oxy
, cho tam giác
ABC
v i ớ
( ) ( )
1; 2 , 2; 11B C− − −
. G iọ
,M N
là các đi m th a mãn ể ỏ
3 , 3AB AM AC AN= =
uuur uuuur uuur uuur
. Hãy tìm t a đ c a véct ọ ộ ủ ơ
MN
uuuur
.
Câu 5 (2,0 đi m=1+1): ể
Cho hàm s ố
( )
2
2 1 2 1y x m x m= − + + +
(v i ớ
m
là tham s th c) (1)ố ự
a) L p b ng bi n thiên và v đ th hàm s (1) khi ậ ả ế ẽ ồ ị ố
1m=
.
b) Tìm t t c các giá tr c a tham s ấ ả ị ủ ố
m
đ đ th hàm s (1) c t tr c hoành t iể ồ ị ố ắ ụ ạ
hai đi m phân bi t ể ệ
,A B
sao cho di n tích tam giác ệ
HAB
b ng 3, v i ằ ớ
H
là
giao đi m c a đ th hàm s (1) và tr c tung.ể ủ ồ ị ố ụ
Câu 6 (2,0 đi m=0,5+0,75+0,75):ể
Cho tam giác
ABC
có chi u cao ề
6 , 3 ,AH a HB a= =
( )
2 0 ,HC a a H= >
n m trên c nhằ ạ
BC
.
a) Phân tích véct ơ
AH
uuur
theo hai véct ơ
,AB AC
uuur uuur
.
b) Tính s đo c a góc ố ủ
ﾷ
BAC
.
c) G i ọ
,D E
l n l t là hình chi u vuông góc c a ầ ượ ế ủ
H
lên
,AB AC
. Tính đ dài ộ
đo n th ng ạ ẳ
DE
theo
a
.
Câu 7 (2,0 đi m=ể1+1):
a) Tìm t t c các giá tr c a tham s th c ấ ả ị ủ ố ự
m
đ ph ng trình sau vô nghi m:ể ươ ệ
1 1
2
x x
x m x
+ −
=
− −
.
b) Cho
0, 0, 6x y x y> > +
. Tìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
6 8
3 2P x y x y
= + + +
.
-------------H t-------------ế
ĐÁP ÁN MÔN TOÁN_KH I 10Ố
Câu N i dungộĐi mể
1a)
:P
”T t c h c sinh c a l p đu thích h c môn Toán”ấ ả ọ ủ ớ ề ọ 0,5
b)
{ }
2;3A B =�
,
{ }
1;2;3;4;5A B =�
0,5
2
a) Đi u ki n ề ệ
0,25
V i đi u ki n đó, pt ớ ề ệ
2
9 3x x= =� �
0,25
b) TH 1:
21
35
3 2 3 2
xx
x x
−
=�
+ = −
0,25
TH 2:
2
5
3
3 2 3 2
xx
x x
< −
= −�
− − = −
Pt đã cho có hai nghi m ệ
1; 5
5
x x= = −
0,25
3T gi thi t ta có h pt ừ ả ế ệ
1
2
4
6
b
a
a b c
c
− =
+ + =
=
0,5
Gi i h ta đc ả ệ ượ
2, 4, 6a b c= = − =
0,5
4
a)
MB MA AB DC DM MC− = = = +
uuur uuur uuur uuur uuuur uuuur
0,5
b)
( )
1
3 3 3 3 3
BC AC AB AN AM AN AM MN MN BC= − = − = − = =�
uuur uuur uuur uuur uuuur uuur uuuur uuuur uuuur uuur
0,25
Mà
( )
3; 9BC = − −
uuur
nên
( )
1; 3MN = − −
uuuur
0,25
5
a) Khi
1m=
, ta có
2
4 3y x x= − +
.
B ng bi n thiên (h c sinh t làm)ả ế ọ ự 0,5
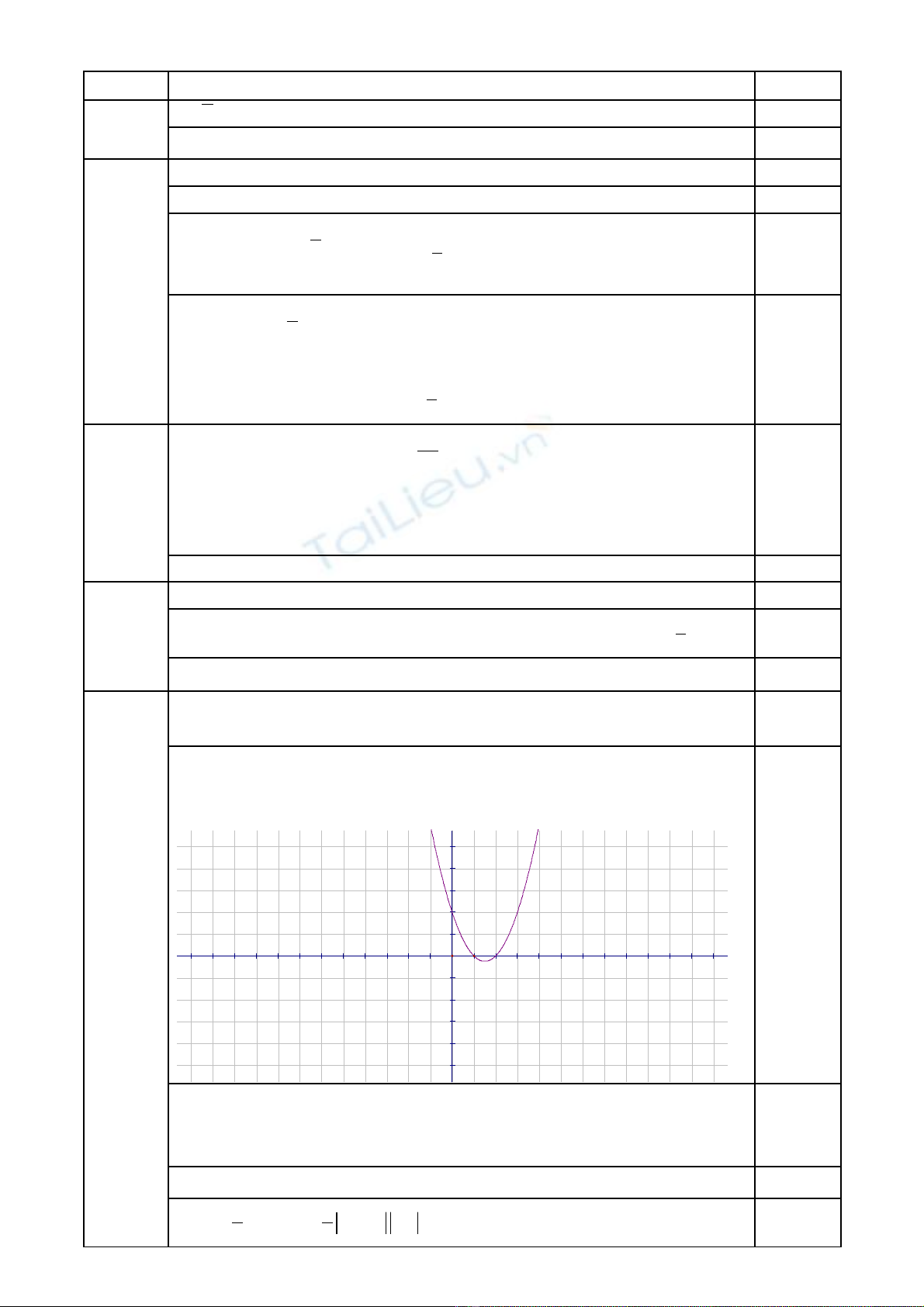
Đ th là đng parabol có đnh ồ ị ườ ỉ
( )
2; 1I−
, tr c đi x ng là ụ ố ứ
đng th ng có pt x=2; parabol c t tr c Ox t i các đi m (1;0), ườ ẳ ắ ụ ạ ể
(3;0); parabol c t tr c tung t i đi m (0;3).ắ ụ ạ ể
4
2
-2
-4
-10
-5
5
10
f
x
=
x
2
-3
x
+2
0,5
b) Pt hoành đ giao đi m:ộ ể
( ) ( )
2
1
2 1 2 1 0 0
2 1
x
x m x m m
x m
=
− + + + = ۹= +
0,25
( )
0;2 1H m +
0,25
1 1
. 2 1 2 3
2 2
HAB
S OH AB m m= = + =
0,25
2
1
2 3 3
2
m
m m m
=
+ =� � = −
0,25
6
a) T gi thi t, ta có ừ ả ế
3
5
BH BC=
uuur uuur
.0,25
( )
3 3 2 3
5 5 5 5
AH AB BH AB BC AB AC AB AB AC= + = + = + − = +
uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur
0,25
b) Áp d ng đnh lí Pitago cho các tam giác vuông HAB, HAC ta ụ ị
đc: ượ
3 5 , 2 10AB a BC a= =
.0,25
T đó ừ
ﾷ
2 2 2 2 2 2
45 40 25 1
os 2 . 2.3 5 .2 10 2
AB AC BC a a a
c BAC AC AB a a
+ − + −
= = =
0,25
V y ậ
ﾷ
45BAC =
o
0,25
c) D a vào ự
2 2
. , .AH AD AB AH AE AC= =
tính đcượ
12 18
,
5 10
a a
AD AE= =
0,25
Áp d ng đnh lí côsin cho tam giác ụ ị
ADE
, ta đcượ
ﾷ
2 2 2
2 2 2
144 18 12 18 2
2 . cos 2. . .
5 10 2
5 10
a a a a
DE AD AE AD AE DAE= + − = + −
0,25
=
2
18 3 2a DE a=�
.0,25
7
a) Đi u ki n: ề ệ
, 2x m x
.
V i đk đó, pt ớ
( ) ( ) ( ) ( )
1 2 1 2x x x m x mx m+ − = − − = +� �
0,5
Pt vô nghi m ệ
0
2 0
m
m
=
+
ho c ặ
0
2
m
m
x m
m
+
= =
ho c ặ
0
22
m
m
xm
+
= =
0,25
{ }
0; 1;2m−� �
0,25
( )
6 8 3 6 1 8 3
3 2 2 2 2
P x y x y x y
x y x y
� �
� �
= + + + = + + + + +
� �
� �
� � � �
0,5
3 6 1 8 3
2 . 2 . .6 19
2 2 2
P x y
x y
+ + =
. 0,25
H n n a khi ơ ữ
2, 4x y= =
(th a mãn) thì ỏ
. V y ậ
min 19P=
khi
2, 4x y= =
0,25