(ĐỀ THI THAM KHẢ O)
BỘ GIÁO DỤ C VÀ ĐÀO TẠ O
TRƯ Ờ NG ĐẠ I HỌ C MỞ TP. HCM
ĐỀ THI TUYỂ N SINH ĐẠ I HỌ C - HỆ VỪ A LÀM VỪ A HỌ C
Môn thi: TOÁN (ĐỀ SỐ 1)
Thờ i gian làm bài: 120 phút, không kể thờ i gian phát đề
Câu I (2 điể m) Tính đạ o hàm củ a các hàm số sau đây:
1. y = (x+2)lnx .
2. y =
sin cosx x x
e
.
Câu II (2 điể m) Cho hàm số y = x3– 3x2 + m2x + m; m là tham số.
1. Khả o sát và vẽ đồ thị (C) củ a hàm số đã cho khi m = 0.
2. Tìm các giá trị củ a m để hàm số có cự c trị .
Câu III (2 điể m) Tính các tích phân sau đây :
1.
( 1)sin 2x xdx
.
2.
5
4
0
xdx
tg
.
Câu IV (2 điể m) Trên mặ t phẳ ng vớ i hệ tọ a độ Đề các Oxy cho các điể m A(1;2),
B(–1;– 1), C(3; –1).
1. Chứ ng minh rằ ng ABC cân tạ i A. Tính diệ n tích ABC.
2. Lậ p phư ơ ng trình các đư ờ ng thẳ ng (AB), (CA).
Câu V (2điể m) Trong không gian vớ i hệ tọ a độ Đề các vuông góc Oxyz cho các
điể m A(0; – 1; 1), B(– 1; 2; 4) và đư ờ ng thẳ ng
d:
1 1
1 2 3
x y z
.
1. Viế t phư ơ ng trình mặ t phẳ ng (P) đi qua A và vuông góc vớ i d.
2. Tìm hình chiế u vuông góc củ a B trên (P).
--------------------------------------------- Hế t ----------------------------------------------
Cán bộ coi thi không giả i thích gì thêm.
Họ và tên thí sinh:……………………………………số báo danh:………………..
ĐÁP ÁN ĐỀ SỐ 1
Câu I (2 điể m = 1 + 1) Tính đạ o hàm củ a các hàm số sau đây:
1. y = (x+2)lnx .
2. y =
sin cosx x x
e
.
Giả i
1. y' = lnx +
2
1x
.
2. y’ =
sin cosx x x
e
(1 + cosx + sinx).
Câu II (2 điể m = 1 + 1) Cho hàm số y = x3– 3x2 + m2x + m (Cm).
1. Khả o sát và vẽ đồ thị (C) củ a hàm số đã cho khi m = 0.
2. Tìm các giá trị củ a m để hàm số có cự c trị .
Giả i
1. Khả o sát hàm số khi m = 0 : y = x3– 3x2 (C)
Tậ p xác đị nh : D = R.
y' = 3x2– 6x = 3x(x – 2).
y’ = 0
0 0;
2 4.
x y
x y
y’’ = 6x – 6 = 6(x – 1).
y’’ = 0 x = 1 y = – 2.
Bả ng biế n thiên
– 0 2 +
+ 0 – 0 +
+
(CĐ)
0
– 4
(CT)
–
Tính lồ i lõm
y’’ = 6x – 6 = 6(x – 1).
y’’ = 0 x = 1 y = – 2.
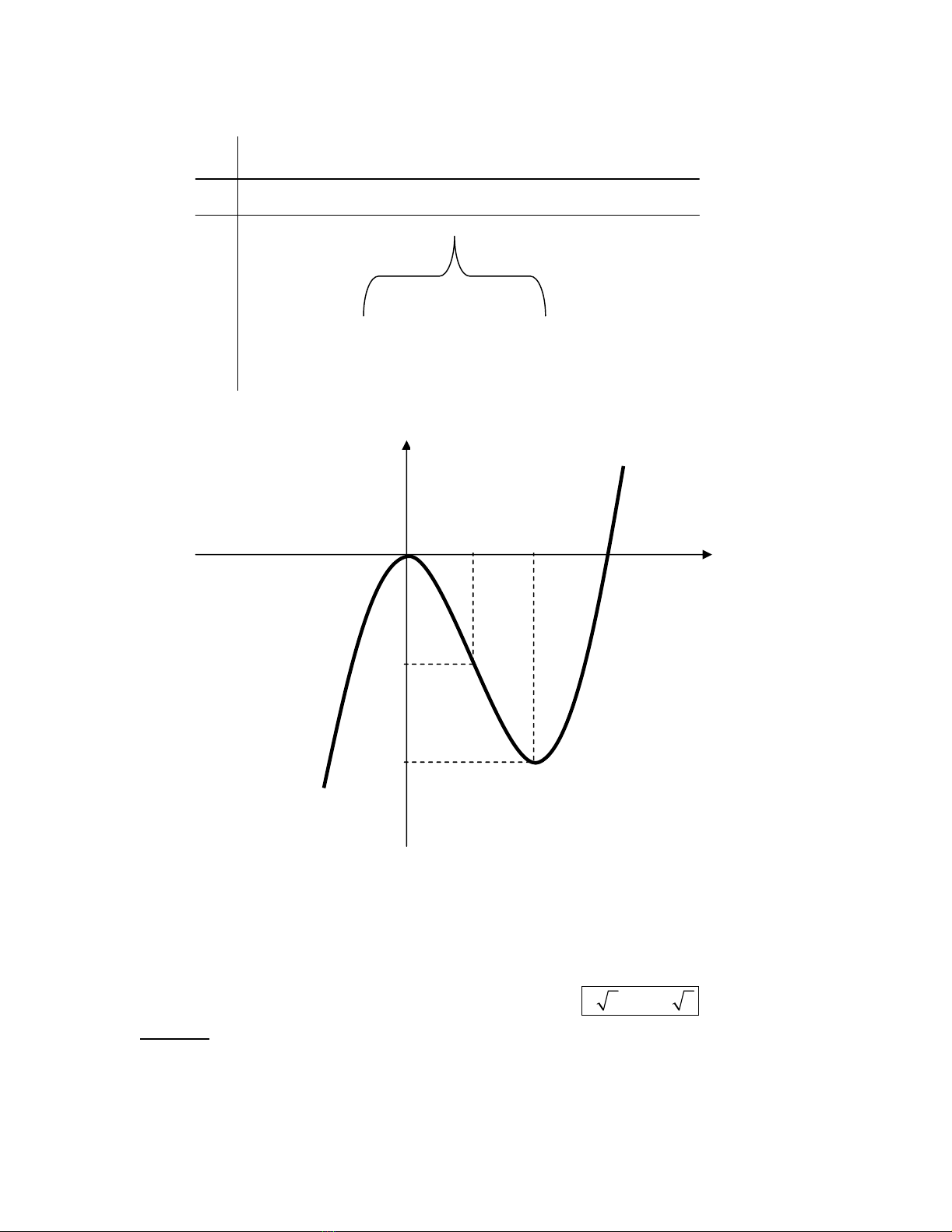
Điể m đặ c biệ t: CĐ(0; 0), CT(2; – 4), ĐU(1; – 2).
Đồ thị (C):
2. Tìm các giá trị củ a m để hàm số có cự c trị .
y' = 3x2– 6x + m2;’ = 3( 3 – m2).
Hàm số có cự c trị khi và chỉ khi y’ có hai nghiệ m phân biệ t và đổ i dấ u hai lầ n
khi x đi qua các nghiệ m. Tứ c là
’ = 3( 3 – m2) > 0
3 3m
.
Câu III (2 điể m = 1 + 1) Tính các tích phân sau đây :
1.
( 1)sin 2x xdx
.
x
y’’
– ∞
+∞
─
+
0
(C)
1
(Điể m uố n)
(
1
;
2
)
lồ i
lõm
0
-2
-4
1
2
2.
5
4
0
xdx
tg
.
Giả i
1. Tính I =
( 1)sin 2x xdx
.
Đặ t u = x – 1; dv = sin2xdx du = dx; v = –
1
2
cos2x.
I =
udv uv vdu
=
1
2
(1 – x)cos2x +
1
2
cos2xdx
=
1
4
[ 2(1 –x)cos2x + sin2x ] + C.
2. Tính J =
5
4
0
xdx
tg
=
5 3 3
4
0
) ( ) ][( x tg x tg x tgx tgx dxtg
=
3 2
4 4
0 0
sin
)( 1) cos
(x
x tgx tg x dx dx
x
tg
=
3
4 4
0 0
(cos )
) ( ) cos
(d x
x tgx d tgx x
tg
=
4 2 4
0
ln cos
4 2
tg x tg x x
=
1
4
(2ln2 –1).
Câu IV (2 điể m = 1 + 1) Trên mặ t phẳ ng vớ i hệ tọ a độ Đề các Oxy cho các điể m
A(1; 2), B(– 1;– 1), C(3; – 1).
1. Chứ ng minh rằ ng ABC cân tạ i A. Tính diệ n tích ABC.
2. Lậ p phư ơ ng trình chính tắ c các đư ờ ng thẳ ng (AB), (CA).
Giả i
1. Chứ ng minh rằ ng
ABC cân tạ i A. Tính diệ n tích
ABC.
AB =
13
= AC (ABC cân tạ i A).
2 3 12
2 3
B B
A A
C A C A
x x y y
x x y y
; dt(ABC) =
12
= 12 (dvdt).
2. Lậ p phư ơ ng trình chính tắ c các đư ờ ng (AB), (CA).
(AB):
B B
B B
A A
x x y y
x x y y
1 1
2 3
x y
.
(CA):
A A
C A C A
x x y y
x x y y
1 2
2 3
x y
.
Câu V (2điể m = 1 + 1) Trong không gian vớ i hệ tọ a độ Đề các vuông góc Oxyz
cho các điể m A(0; – 1; 1), B(– 1; 2; 4) và đư ờ ng thẳ ng
d:
1 1
1 2 3
x y z
.
1. Viế t phư ơ ng trình mặ t phẳ ng (P) đi qua A và vuông góc vớ i d.
2. Tìm hình chiế u vuông góc củ a B trên (P).
Giả i
1. Viế t phư ơ ng trình mặ t phẳ ng (P) đi qua A và vuông góc vớ i d.
(P) có vectơ pháp tuyế n chính là vectơ chỉ phư ơ ng củ a d:
Pd
n v
= (1; 2; 3)
Phư ơ ng trình củ a (P) là:
(x – 0) + 2(y + 1) + 3(z – 1) = 0 x + 2y + 3z –1 = 0.
2. Tìm hình chiế u vuông góc củ a B trên (P).
Gọ i H là hình chiế u vuông góc củ a B trên (P). Đư ờ ng thẳ ng (BH) nhậ n
d
v
làm vectơ chỉ phư ơ ng nên có phư ơ ng trình tham số như sau: x = –
1+ t, y = 2 + 2t, z = 4 + 3t.
H là giao điể m củ a (BH) vớ i (P). Tọ a độ củ a H xác đị nh bở i hệ
1 ;
2 2 ;
4 3 ;
2 3 1 0.
x t
y t
z t
x y z
Giả i hệ ta đư ợ c H( 0 –2; 0; 1).