SỞ GIÁO DỤC KHOA HỌC VÀ CÔNG NGHỆ
BẠC LIÊU
--------------
ĐỀ CHÍNH THỨC
KỲ THI TUYN SINH L"P 10 THPT
NĂM HC 2019 – 2020
Môn thi: TOÁN (Không chuyên)
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Ngày thi: 07/6/2019
-------------------
ð BÀI
Câu 1:(4,0 ñi8m) Rút g(n bi+u th-c:
a) 45 2 20A= −
b)
( )
2
3 5 27 3 12
3 5
B−
= − −
−.
Câu 2:(4,0 ñi8m)
a) Gi5i h6 phương trình 2 4
5
x y
x y
− =
+ =
b) Cho hàm s?
2
3y x= có ñB thC
( )
P
và ñưEng thFng
( )
: 2 1d y x= +
. Tìm t(a ñH gia0 ñi+m cIa
( )
P
và
( )
d
bJng phép tính.
Câu 3:(6,0 ñi8m)
Cho phương trình:
( )
2
2 4 5 1x mx m− − −
(m là tham s?).
a) Gi5i phương trình
( )
1
khi
2m= −
.
b) Ch-ng minh phương trình
( )
1
luôn có nghi6m vQi m(i giá trC cIa m.
c) G(i
1
x;
2
x là hai nghi6m cIa phương trình
( )
1
. Tìm m ñ+:
( )
2
1 1 2
1 33
1 2 762019
2 2
x m x x m− − + − + =
.
Câu 4:(6,0 ñi8m)
Trên nUa ñưEng tròn ñưEng kính AB, lXy hai ñi+m I, Q sao cho I thuHc cung AQ. G(i C là giao
ñi+m hai tia AI và BQ; H là giao ñi+m hai dây AQ và BI.
a) Ch-ng minh t- giác CIHQ nHi ti\p.
b) Ch-ng minh:
. .CI AI HI BI=
.
c) Bi\t
2AB R=
. Tính giá trC bi+u th-c:
. .M AI AC BQ BC= +
theo R.
^^^^^^^^^^^H<t^^^^^^^^^^^
HƯ"NG DDN GIEI.
Câu 1:(4,0 ñi8m) Rút g(n bi+u th-c:
a)
45 2 20
A= −
b)
( )
2
3 5 27
3 12
3 5
B−
= − −
−
GiFi:
a) 2 2
45 2 20 3 .5 2 2 .5 3 5 2.2 5 5
A
= − = − = − = −
b)
( )
2
3 5 27 3 5 3 3
3 12 3 12
3 5 3 5
B− −
= − − = − −
− −
(
)
( )
3 5 3
3 5
−
= − − +
− (do
2
3 12 3 12
< ⇒ <
)
3 3 12 12 2 3
= − + − = − = − .
Câu 2:(4,0 ñi8m)
a) Gi5i h6 phương trình
2 4
5
x y
x y
− =
+ =
b) Cho hàm s?
2
3
y x
= có ñB thC
(
)
P
và ñưEng thFng
(
)
: 2 1
d y x
= +
. Tìm t(a ñH giao ñi+m cIa
(
)
P
và
(
)
d
bJng phép tính.
GiFi:
a)
2 4 3 9 3
5 5 2
x y x x
x y y x y
− = = =
⇔ ⇔
+ = = − =
V_y h6 phương trình có nghi6m là:
(
)
(
)
; 3;2
x y =
b) Phương trình hoành ñH giao ñi+m:
(
)
2 2
3 2 1 3 2 1 0 *
x x x x= + ⇔ − − =
Phương trình
(
)
*
có h6 s?:
3; 2; 1 0
a b c a b c
= = − = − ⇒ + + =
⇒
Phương trình
(
)
*
có hai nghi6m:
1 2
1
1;
3
c
x x
a
−
= = =
^ VQi
(
)
2
1
1 3.1 3 1;3
x y A= ⇒ = = ⇒
^ VQi
2
2
1 1 1 1 1
3. ;
3 3 3 3 3
x y B
− − −
= ⇒ = = ⇒
V_y t(a ñH giao ñi+m cIa
(
)
P
và
(
)
d
là
(
)
1;3
A
và
1 1
;
3 3
B−
.
Câu 3:(6,0 ñi8m)
Cho phương trình:
(
)
2
2 4 5 1
x mx m− − −
(m là tham s?).
a) Gi5i phương trình
(
)
1
khi
2
m
= −
.
b) Ch-ng minh phương trình
(
)
1
luôn có nghi6m vQi m(i giá trC cIa m.
c) G(i
1
x
;
2
x
là hai nghi6m cIa phương trình
(
)
1
. Tìm m ñ+:
( )
2
1 1 2
1 33
1 2 762019
2 2
x m x x m− − + − + =
GiFi:
a) Thay
2
m
= −
vào phương trình
(
)
1
ta có:
( ) ( ) ( )( )
2
3
4 3 0 3 3 0 3 1 0
1
x
x x x x x x x x
= −
+ + = ⇔ + + + = ⇔ + + = ⇔
= −
V_y vQi
2
m
= −
thì phương trình có t_p nghi6m
{
}
3; 1
S
= − −
b) Ta có:
( ) ( )
2
' 2
4 5 2 1 0,
m m m m
= − − − = + + > ∀
Do ñó phương trình
(
)
1
luôn có hai nghi6m vQi m(i giá trC cIa m.
c) Do phương trình
(
)
1
luôn có hai nghi6m vQi m(i giá trC cIa m, g(i
1 2
;
x x
là hai nghi6m cIa
phương trình
(
)
1
Áp dcng ñCnh lí Vi^ét ta có: 1 2
1 2
2
4 5
x x m
x x m
+ =
= − −
Ta có:
( )
2
1 1 2
1 33
1 2 762019
2 2
x m x x m− − + − + =
(
)
( )
1
1
2
1 2
2
1 1 2
2 1 2 4 33 1524038
2 4 5 2 1524000
x m x x m
x mx m x x
⇔ − − + − + =
⇔ − − − + + =
(
)
1 2
2 1524000
x x⇔ + =
(do
1
x
là nghi6m cIa
(
)
1
nên
1
2
1
2 4 5 0
x mx m
− − − =
)
2.2 1524000 381000
m m
⇔ = ⇔ =
V_y
381000
m
=
thea mãn yêu cgu bài toán.
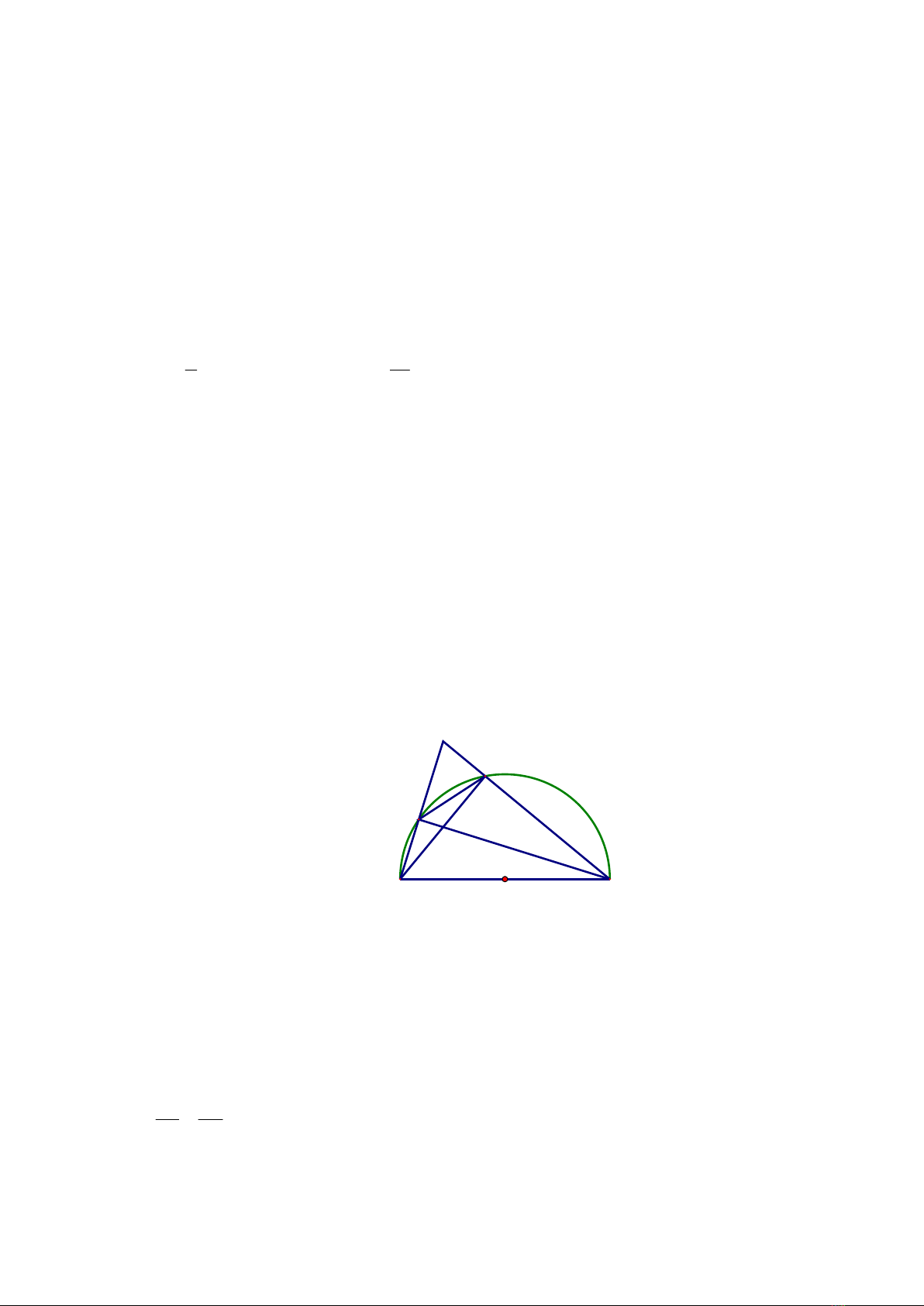
Câu 4:(6,0 ñi8m)
Trên nUa ñưEng tròn ñưEng kính AB, lXy hai ñi+m I, Q sao cho I thuHc cung AQ. G(i C là giao
ñi+m hai tia AI và BQ; H là giao ñi+m hai dây AQ và BI.
a) Ch-ng minh t- giác CIHQ nHi ti\p.
b) Ch-ng minh:
. .
CI AI HI BI
=
.
c) Bi\t
2
AB R
=
. Tính giá trC bi+u th-c:
. .
M AI AC BQ BC
= +
theo R.
GiFi:
a) Ta có:
0
90
AIB AQB= =
(góc nHi ti\p chhn nUa ñưEng tròn)
0
90
CIH CQH⇒ = =
Xét t- giác CIHQ có
0 0 0
90 90 180
CIH CQH+ = + =
⇒
t- giác CIHQ nHi ti\p
b) Xét
AHI
và
BCI
có:
( )
0
90
.
AIH BIC
AHI BCI g g
IAH IBC
= = ⇒
=
∽
∽∽
∽
. .
AI HI
CI AI HI BI
BI CI
⇒ = ⇒ =
c) Ta có:
(
)
(
)
. .
M AI AC BQ BC AC AC IC BQ BQ QC
= + = − + +
H
Q
C
I
OB
A
( )
( )
2 2
2 2 2
2 2
2
. .
. .
.
. .
AC AC IC BQ BQ QC
AQ QC AC IC BQ BQ QC
AQ BQ QC QC BQ AC IC
AB QC BC AC IC
= − + +
= + − + +
= + + + −
= + −
T- giác AIBQ nHi ti\p
(
)
O
CIQ CBA
⇒ =
(cùng phc vQi
AIQ
)
Xét
CIQ
và
CBA
có:
( )
.
ACB chung
CIQ CBA g g
CIQ CBA
⇒
=
∽
∽∽
∽
. .
. . 0
IC QC
QC BC AC IC
BC AC
QC BC AC IC
⇒ = ⇒ =
⇒ − =
Suy ra:
( )
2
2 2
2 4
M AB R R
= = =
^^^^^^^^^^^ HẾT ^^^^^^^^^^^