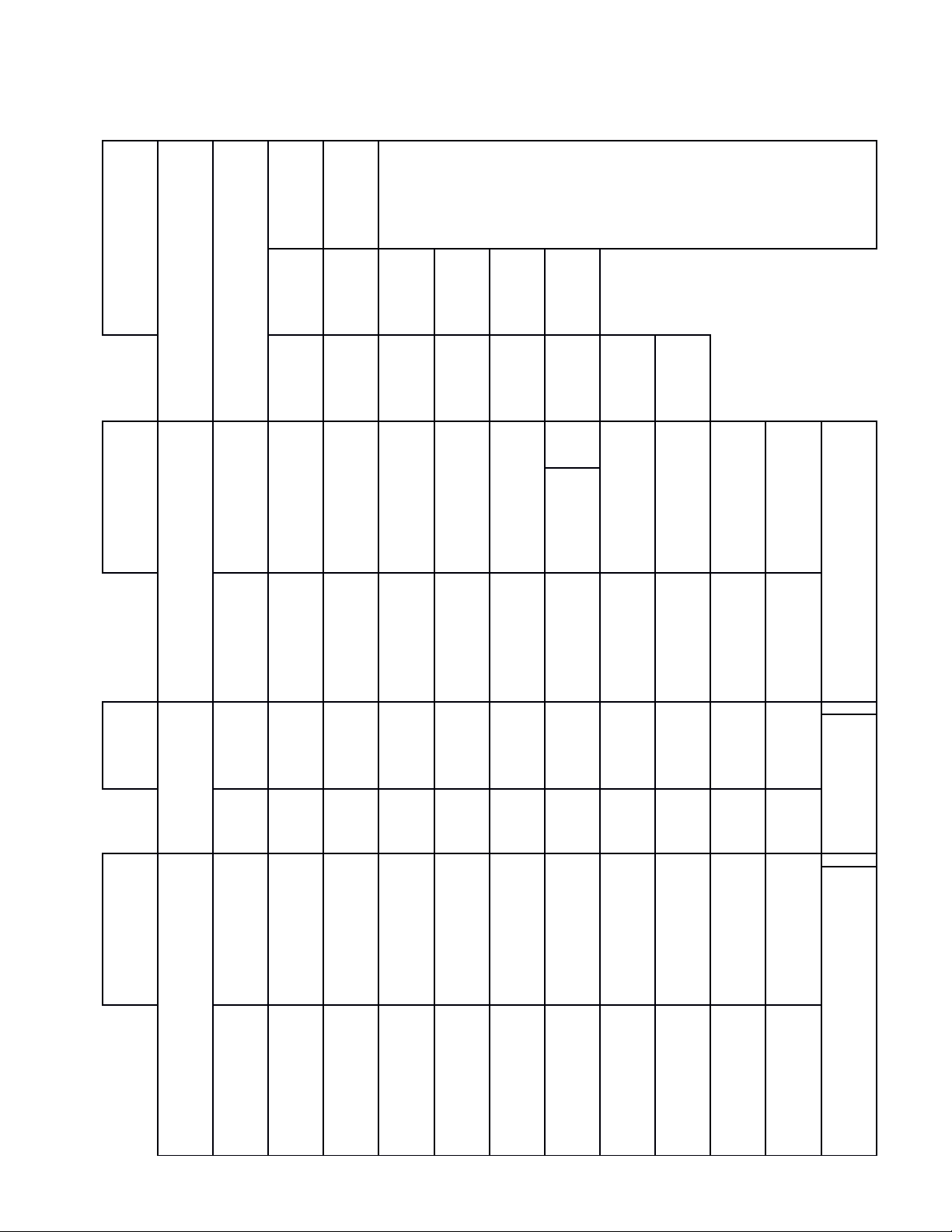
MA TRẬN ĐỀ THI TUYỂN SINH VÀO 10 THPT
MÔN TOÁN (CHUYÊN) – THỜI GIAN LÀM BÀI 150 PHÚT
TT Nội
dun
g
kiến
thức
Đơn
vị
kiến
thức
Mức
độ
nhậ
n
thức
Tổn
g% tổng điểm
Nhậ
n
biết
Thô
ng
hiểu
Vận
dụn
g
Vận
dụn
g
cao
Số
câu
hỏi Thời
gian
(phú
t)
Số
câu
hỏi
Thời
gian
(phú
t)
Số
câu
hỏi
Thời
gian
(phú
t)
Số
câu
hỏi
Thời
gian
(phú
t)
Số
câu
hỏi
Thời
gian
(phú
t)
1
Biến
đổi
đại
số
1.
Tính
giá
trị
của
biểu
thức
0 0 0 0 1 10 0 0 1 10
20
2.
Giải
hệ
phư
ơng
trình
0 0 0 0 1 10 0 0 1 10
2
Đa
thức
1.
Bất
đẳng
thức.
0 0 0 0 0 0 1 15 1 10
20
2.
Đa
thức
0 0 0 0 1 10 0 0 1 10
3 Số
học
1. Số
chín
h
phư
ơng,
hợp
số
0 0 0 0 0 0 1 10 1 10
15
2.
Phư
ơng
trình
nghi
ệm
nguy
0 0 0 0 0 0 1 15 1 15
ên
4
Hìn
h
học
Hình
học
phẳn
g
0 0 0 0 1 15 2 30 3 45 30
5
Toá
n
rời
rạc,
suy
luận
logic
1.
Suy
luận
logic
0 0 0 0 0 0 1 15 1 10 7,5
2.
Suy
luận
logic
, quy
nạp
0 0 0 0 0 0 1 15 1 15 7,5
Tổn
g0 0 0 0 4 45 7 105 11 150 100
Tỉ lệ
(%) 0 0 40 60 100
Tỉ lệ chung (%) 040 60
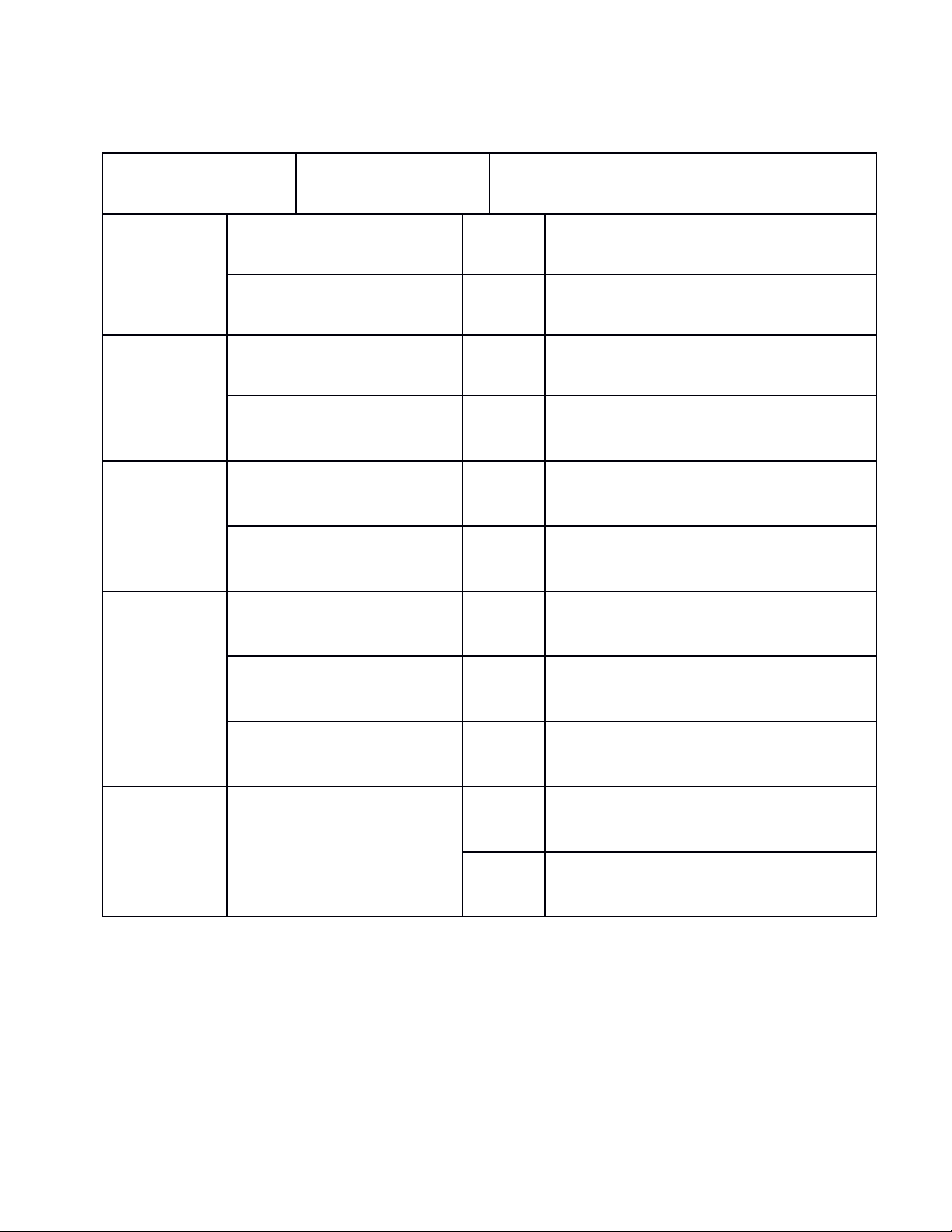
BẢNG ĐẶC TẢ ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT
MÔN TOÁN (CHUYÊN) – THỜI GIAN LÀM BÀI 150 PHÚT
CHỦ ĐỀ MỨC ĐỘ MÔ TẢ
Biến đổi đại
số
Áp dụng các hằng đẳng thức,
biến đổi đại số.
Vận
dụng
Biến đổi đại số nhằm tính giá trị biểu
thức.
Giải hệ phương trình Vận
dụng
Vận dụng thành thạo các phương pháp
giải hệ phương trình.
Đa thức. Bất
đẳng thức
Đa thức Vận
dụng
Vận dụng định lý Bezout, linh hoạt trong
các phép biến đổi.
Bất đẳng thức.
Vận
dụng
cao
Vận dụng thành thạo các phương pháp
chứng minh bất đẳng thức.
Số học
Số chính phương, hợp số
Vận
dụng
cao
Vận dụng thành thạo các tính chất của số
chính phương, hợp số.
Phương trình nghiệm nguyên
Vận
dụng
cao
Vận dụng các phương pháp giải phương
trình nghiệm nguyên.
Hình học
phẳng
Góc nội tiếp; Góc tạo bởi
tiếp tuyến và dây cung; Tứ
giác nội tiếp.
Vận
dụng
Vận dụng các kiến thức về góc trong
đường tròn, tứ giác nội tiếp để chứng
minh tứ giác nội tiếp.
Đường tròn ngoại tiếp,
đường tròn nội tiếp, tứ giác
nội tiếp.
Vận
dụng
Vận dụng tính chất của góc trong đường
tròn, tam giác đồng dạng, tứ giác nội tiếp
để chứng minh đẳng thức hình học.
Tam giác đồng dạng, góc nội
tiếp, tứ giác nội tiếp
Vận
dụng
cao
Vận dụng thành thạo các kiến thức hình
học để chứng minh bài toán tỉ số không
đổi.
Toán rời rạc,
suy luận
logic
Suy luận logic. Nguyên lý
dirichlet, Toán tô màu. Quy
nạp
Vận
dụng
cao
Vận dụng linh hoạt, suy luận logic.
Vận
dụng
cao
Vận dụng linh hoạt, suy luận logic, quy
nạp toán học.
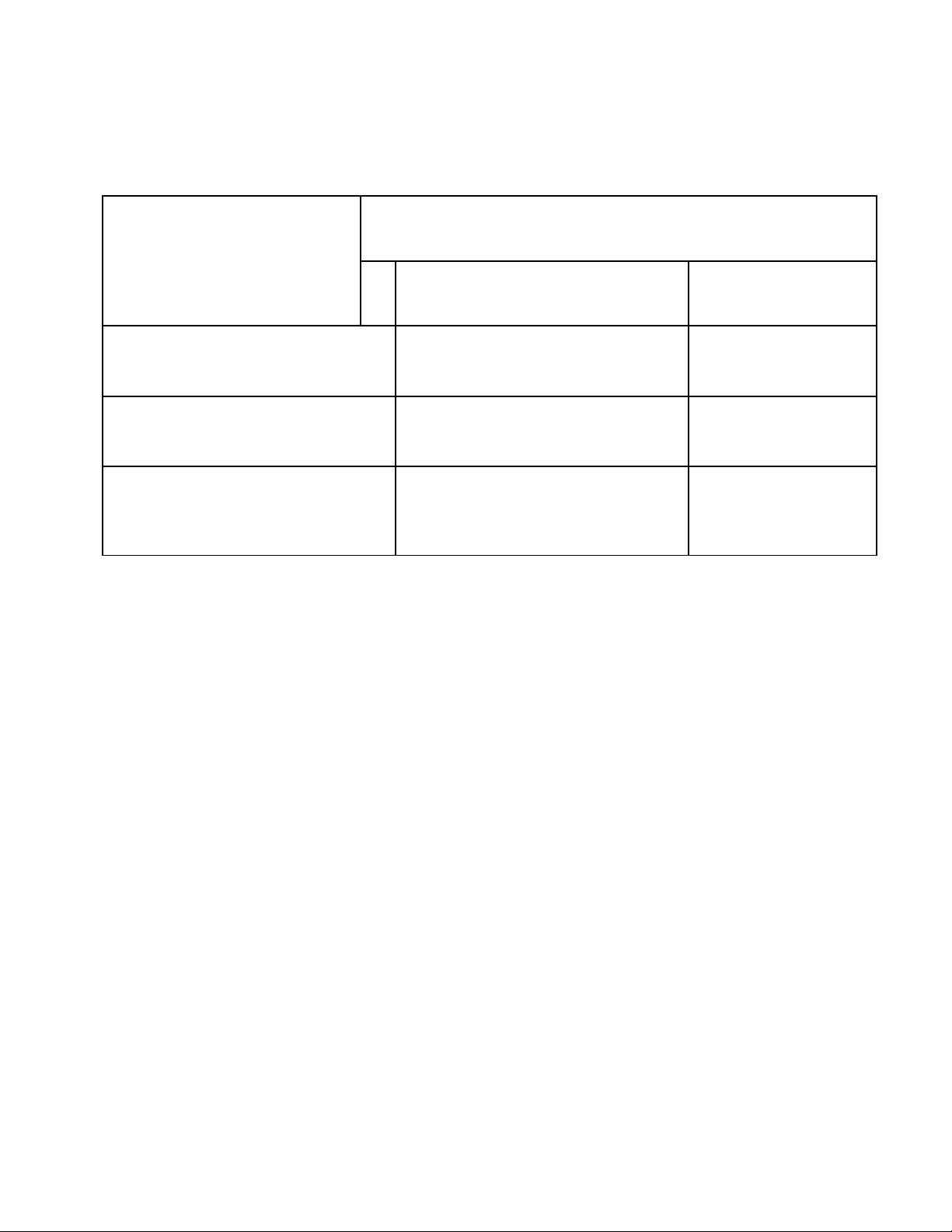
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY ĐỀ THI TUYỂN SINH 10 THPT
Môn: TOÁN (CHUYÊN)
Năng lực
Cấp độ tư duy
Vận dụng Vận dụng cao
Tư duy và lập luận Toán học 4
(Câu 1a,b; 3a,b)
1
(Câu 3c)
Giải quyết vấn đề Toán học 1
(Câu 2a)
5
(Câu 2b; 4a,b; 5a,b)
Tổng
(Số lệnh hỏi của từng cấp độ tư duy)
5 6
SỞ GD & ĐT NINH BÌNH ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT
Năm 2024
MÔN: TOÁN (CHUYÊN)
Thời gian làm bài: 150 phút
(Đề thi gồm 05 câu, 01 trang)
Câu 1 (2,0 điểm)
a) Cho là các số nguyên dương thỏa mãn . Tính giá trị biểu thức
.
b) Giải hệ phương trình .
Câu 2 (2,0 điểm)
a) Tìm tất cả các đa thức có hệ số thực thỏa mãn và
.
b) Cho thỏa mãn . Chứng minh rằng
.
Câu 3 (3,0 điểm) Cho tam giác nội tiếp đường tròn tâm , là điểm bất kì thuộc cạnh ( khác và ). Gọi ,
lần lượt là trung điểm của các cạnh và . Đường thẳng cắt đường tròn tại , (theo thứ tự P, M, N,
Q). Đường tròn ngoại tiếp tam giác cắt tại (khác ). Các đường thẳng và cắt nhau tại .
a) Chứng minh điểm A, I, P, K nằm trên một đường tròn.
b) Chứng minh .
c) Đường thẳng cắt đường tròn ngoại tiếp tam giác tại (khác ). Đường thẳng cắt đường thẳng tại .
Chứng minh khi di chuyển trên đoạn thì tỉ số không đổi.
Câu 4 (1,5 điểm)
a) Chứng minh rằng nếu tồn tại số nguyên dương x thỏa mãn là một số chính phương thì x là hợp
số.
b) Tìm tất cả các cặp số nguyên dương thỏa mãn
Câu 5 (1,5 điểm) Ban đầu trên bàn có một đống có n viên bi với . A và B cùng chơi một trò chơi như
sau: ở mỗi lượt của mình, người chơi chia một đống bi có mặt trên bàn thành hai đống nhỏ hơn (mỗi
đống phải có ít nhất một viên bi). Người thắng cuộc là người chơi mà trong lượt chơi của mình có thể
làm cho tất cả các đống bi có tối đa hai viên bi. A là người đi trước.
a) Với , chứng minh A có chiến thuật để thắng cuộc.
b) Với , chứng minh B có chiến thuật để thắng cuộc.
------------Hết----------