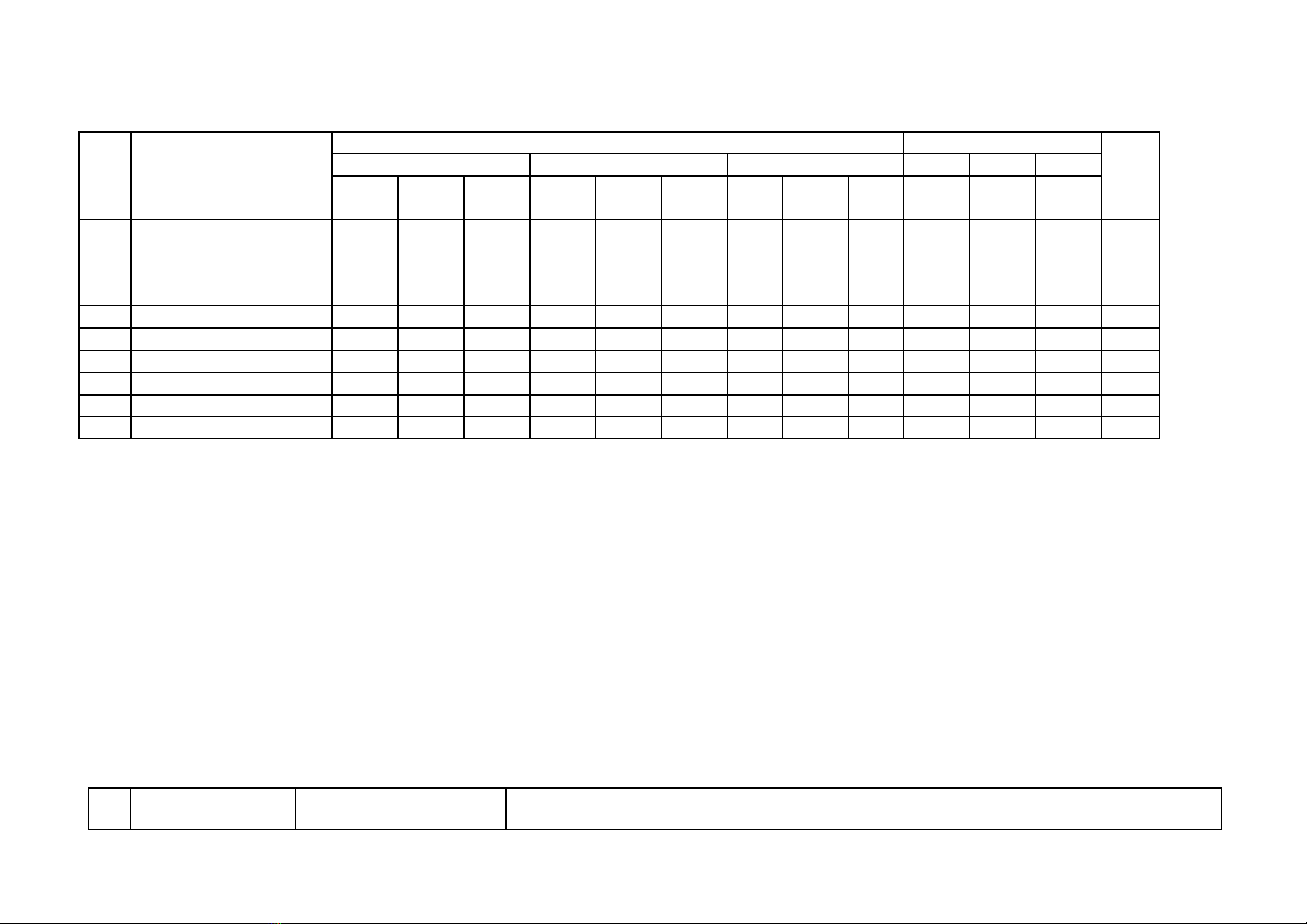
MA TRẬN ĐỀ THI TUYỂN SINH LỚP 10 THPT - MÔN: TOÁN CHUYÊN
TT Nội dung kiến thức
Mức độ nhận thức Tổng Tỉ lệ
%
tổng
điểm
Thông hiểu Vận dụng Vận dụng cao
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
Số
CH
Số
điểm
Thời
gian
1
Rút gọn biểu thức nhiều
biến có điều kiện liên hệ
giữa các biến
1 1 10 1 1 10 10
2Hệ Phương trình 1 1 10 1 1 15 10
3Đa thức 1 1 10 1 1 15 10
4Bất đẳng thức 1 1 25 1 1 25 10
5Hình học phẳng 1 1 10 1 1 10 1 1 15 3 3 35 30
6Số học 1 1 10 1 0,5 15 2 1,5 25 15
7Tổ hợp 1 1 10 1 0,5 15 2 1,5 25 15
BẢN ĐẶC TẢ ĐỀ THI
câ
u
Nội dung kiến thức Đơn vị kiến thức Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá
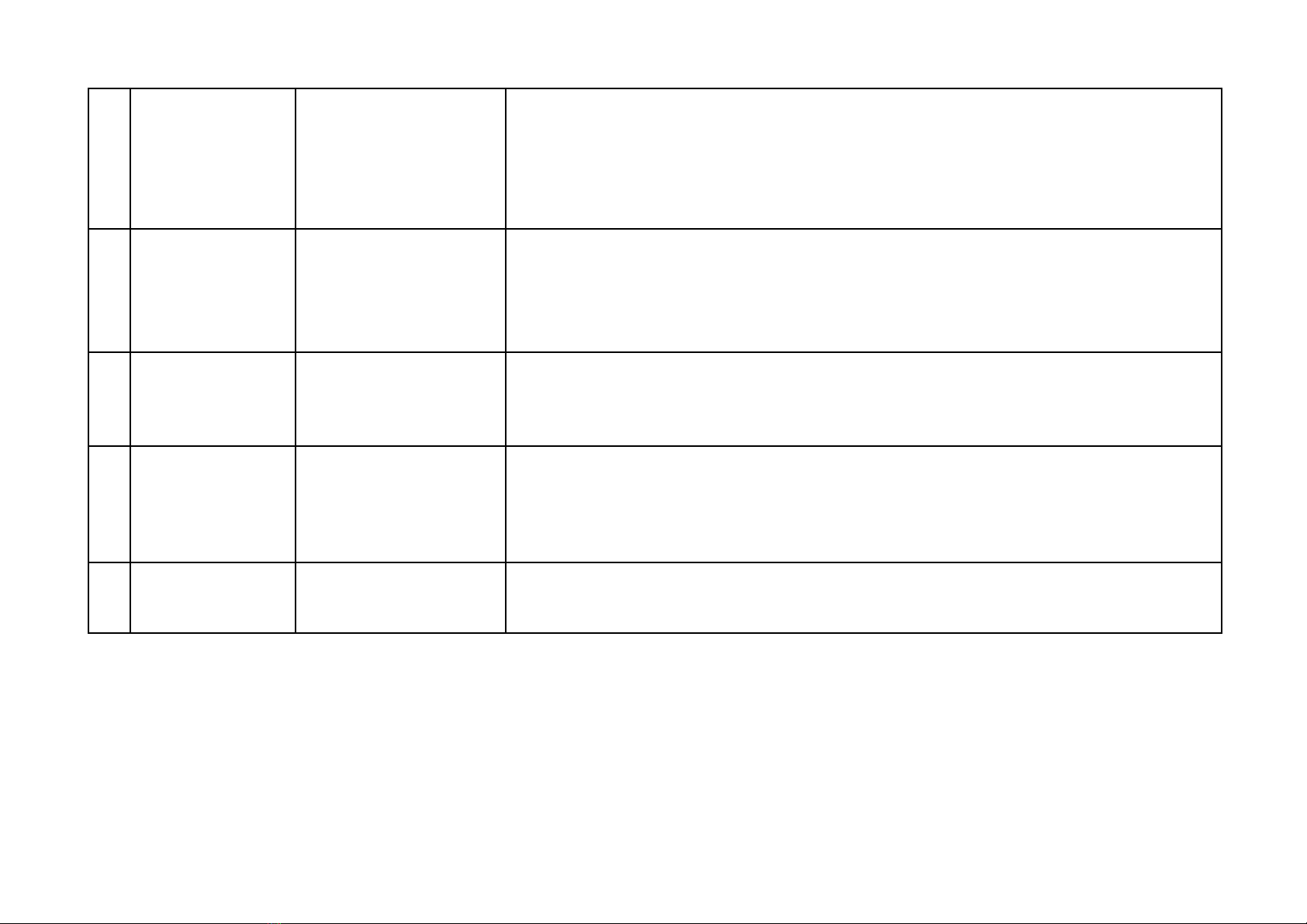
1
- Tính giá trị biểu
thức, có yếu tố
căn bậc hai.
- Hệ phương trình
-Tính giá trị biểu thức.
- Hệ phương trình
không mẫu mực
- Kĩ năng biến đổi biểu thức
- Kỹ năng dùng hằng đẳng thức biến đổi 1 trong hai PT của hệ PT thành dạng luỹ thừa
cùng bậc ở 2 vế, sử dụng phương pháp thế.
2-Đa thức.
-Bất đẳng thức
- Đa thức có hệ số
nguyên.
-Tìm GTLN của biểu
thức có ĐK.
- Sử dụng hệ quả định lí Bơdu. Kĩ năng biến đổi đại số các đa thức một biến.
- Kĩ năng tách hạng tử để có thể áp dụng BĐT quen thuộc.
3Số học
- Chứng minh bài toán
liên quan đến số
nguyên tố.
- Số chính phương
Kĩ năng sử dụng linh hoạt các tính chất chia hết trong tập hợp số nguyên.
4Hình học phẳng. Hình học phẳng.
-Vận dụng hệ thức lượng trong tam giác, trong đường tròn.
-Vận dụng tính chất góc nội tiếp, tỉ số lượng giác , tứ giác nội tiếp, tam giác đồng
dạng,…vào việc chứng minh sự bằng nhau, hệ thức hình học, xác định vị trí của một
điểm.
5Tổ hợp
-Cấu tạo số, chia hết
- Nguyên lí Dỉichlet
Phân chia trường hợp và suy luận logic.
BẢNG NĂNG LỰC VÀ CẤP ĐỘ TƯ DUY ĐỀ THI TUYỂN SINH 10 THPT CHUYÊN
Môn: TOÁN
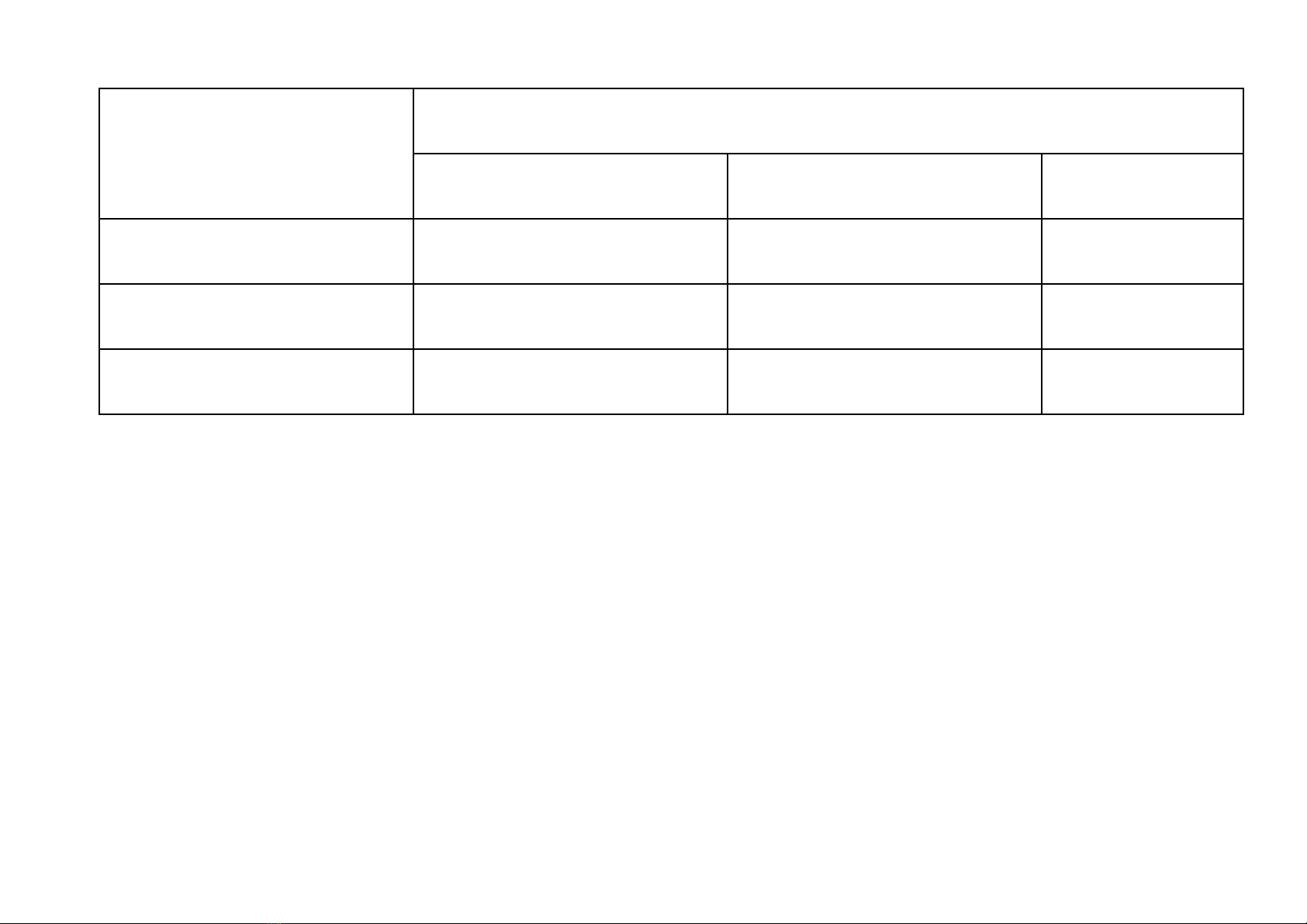
Năng lực
Cấp độ tư duy
Thông hiểu Vận dụng Vận dụng cao
Tư duy và lập luận Toán học 2
(Câu 1a, 4a)
1
(Câu 4b) 0
Giải quyết vấn đề Toán học 1
(Câu 1b)
3
(Câu 2a, 3a, 5a)
4
(Câu 2b, 4c, 3b, 5b)
Tổng
(Số lệnh hỏi của từng cấp độ tư duy) 3 4 4
PHO]NG GD&ĐT TP TAM ĐIÊ_P ĐỀ THI TUYỂN SINH CHUYÊN LỚP 10
Năm 2024
MÔN: TOAdN
Thời gian làm bài:150 phút (không kể thời gian phát đề)
Đề thi gồm 05 câu trong 01 trang
Câu 1 (2,0 điểm).
a) Cho
=2a b
−
. Tính giá trị của biểu thức:
( ) ( ) ( )
2 2
1 – –1 2023 – 3 – 675B a a b b ab ab a b
= + + +
b) Giải hệ phương trình:
2 2
2 2
x y xy 2
x y 2x 4y
+ + =
+ = +
Câu 2 (2,0 điểm).
a) Đa thức P(x) chia cho
3 2x
−
có số dư là 5, chia cho
2x
+
có số dư là 12. Tìm dư
khi chia đa thức P(x) cho
b)Cho a, b, c là các số thực dương thoả mãn:
abc 1
=
Tìm giá trị lớn nhất của biểu thức:
3
1
P1 1
a 2b 3 b 2c 3 c 2a
+ +
+ + + + + +
=
Câu 3 (1,5 điểm).
a)Cho hai số tự nhiên a, b thoả mãn điều kiện:
2 2
a a 2b b
+ = +
. Chứng minh rằng
a b−
và
a b 1
+ +
đều là các số chính phương.
b)Tìm số nguyên tố p sao cho các số
2 2 2
2p 1;2p 3;3p 4
− + +
đều là số nguyên tố.
Câu 4 (3,0 điểm).
Cho đường tròn
( )
O; R
đường kính BC. Gọi A là điểm thoả mãn tam giác ABC nhọn. AB,
AC cắt đường tròn trên tại điểm thứ hai tương ứng là E và D. Trên cung không chứa D
lấy F
( )
F B, C
. AF cắt BC tại M, cắt đường tròn
( )
O; R
tại N
( )
N F
và cắt đường
tròn ngoại tiếp tam giác ADE tại P
( )
P A
.
a) Giả sử
ﾷ
BAC 60
=
. Tính DE theo R.
b) Chứng minh
AN.AF AP.AM
=
c) Gọi I, H thứ tự là hình chiếu vuông góc của F trên các đường thẳng BD, BC. Các đường
thẳng IH và CD cắt nhau ở K. Tìm vị trí của F trên cung để biểu thức
BC BD CD
FH FI FK
+ +
đạt giá trị nhỏ nhất.
Câu 5 (1,5 điểm).
a)Cho n là số nguyên dương có chữ số tận cùng bằng 3. Chứng minh rằng có một số nguyên
dương m chia hết cho n sao cho trong biểu diễn thập phân của số m chỉ xuất hiện chữ số 1.
b) Cho 121 điểm phân biệt nằm trong hoặc trên các cạnh của một tam giác đều có cạnh
bằng 6 cm. Chứng minh rằng có thể vẽ được một hình tròn đường kính bằng
3
cm chứa ít
nhất 11 điểm trong số các điểm đã cho.
-----------Hêdt----------
PHO]NG GD&ĐT TP TAM ĐIÊ_P HƯỚNG DẪN CHẤM ĐÊ] THI TUYỂN SINH
CHUYÊN LỚP 10
Năm 2024
MÔN: TOÁN
(Hươ-ng dâ/n châ-m gô0m 06 trang)
Câu Nội dung Điểm
Câu 1
(2,0 điểm)
a) ( 1,0 điểm)
( )
3 3 2 2
2023 2025 3 B a b a b ab ab ab a b
= − + + + − − −
( )
3 3 2 2
3 2a b ab a b a b ab
= − − − + + −
( ) ( )
3 2
8 4 12a b a b= − + − = + =
b) ( 1,0 điểm)
( )
( )
( ) ( )
( )
2 2
2 2
2 2
3 3
2 2 2
2
x y xy 2 2xy
x y xy 2
x y x y xy 2x 4y
x y 2x 4y
x y 2 2xy 2x 4y
y 0
x y xy y 0 y x xy 1 0 x xy 1 0
+ − = −
+ + =
+ + − = +
+ = +
+ − = +
=
+ + = + + = + + =
+) Với
y 0 x 2
= =
.
+) Với
2 2
x xy 1 0 x xy 1
+ + = + = −
2 2
y 3 y 3 x 3x 1 0
= + = =
có
0
∆ <
phương trình vô
nghiệm.
Vậy hệ phương trình có nghiệm là
( )
( ) ( )
x; y 2;0 , 2;0
= −
.
0,5
0,5
0,25
0,25
0,25
0,25
Câu 2
(2,0 điểm)
a) ( 1,0 điểm)
Dư nếu có khi chia đa thức P(x) cho
là
ax b
+
( )
( )
2
( ) 2 6 ( ) 2 (3 2 ) ( )P x x x q x ax b x x q x ax b
= − − + + = − + − + +
Theo bài ra:
0,25
0,25
0,25