SỞ GIÁO DỤC & ĐÀO TẠO KỲ THI TUYỂN SINH VÀO
LỚP 10
TP ĐÀ NẲNG Khóa ngày 23 tháng 06 năm
2009
MÔN: TOÁN
( Thời gian 120 phút, không kể thời gian giao đề )
Bài 1. ( 3 điểm )
Cho biểu thức
a 1 1 2
K :
a 1
a 1 a a a 1
a) Rút gọn biểu thức K.
b) Tính giá trị của K khi a = 3 + 2
2
c) Tìm các giá trị của a sao cho K < 0.
Bài 2. ( 2 điểm ) Cho hệ phương trình:
mx y 1
x y
334
2 3
a) Giải hệ phương trình khi cho m = 1.
b) Tìm giá trị của m để phương trình vô nghiệm.
Bài 3. ( 3,5 điểm )
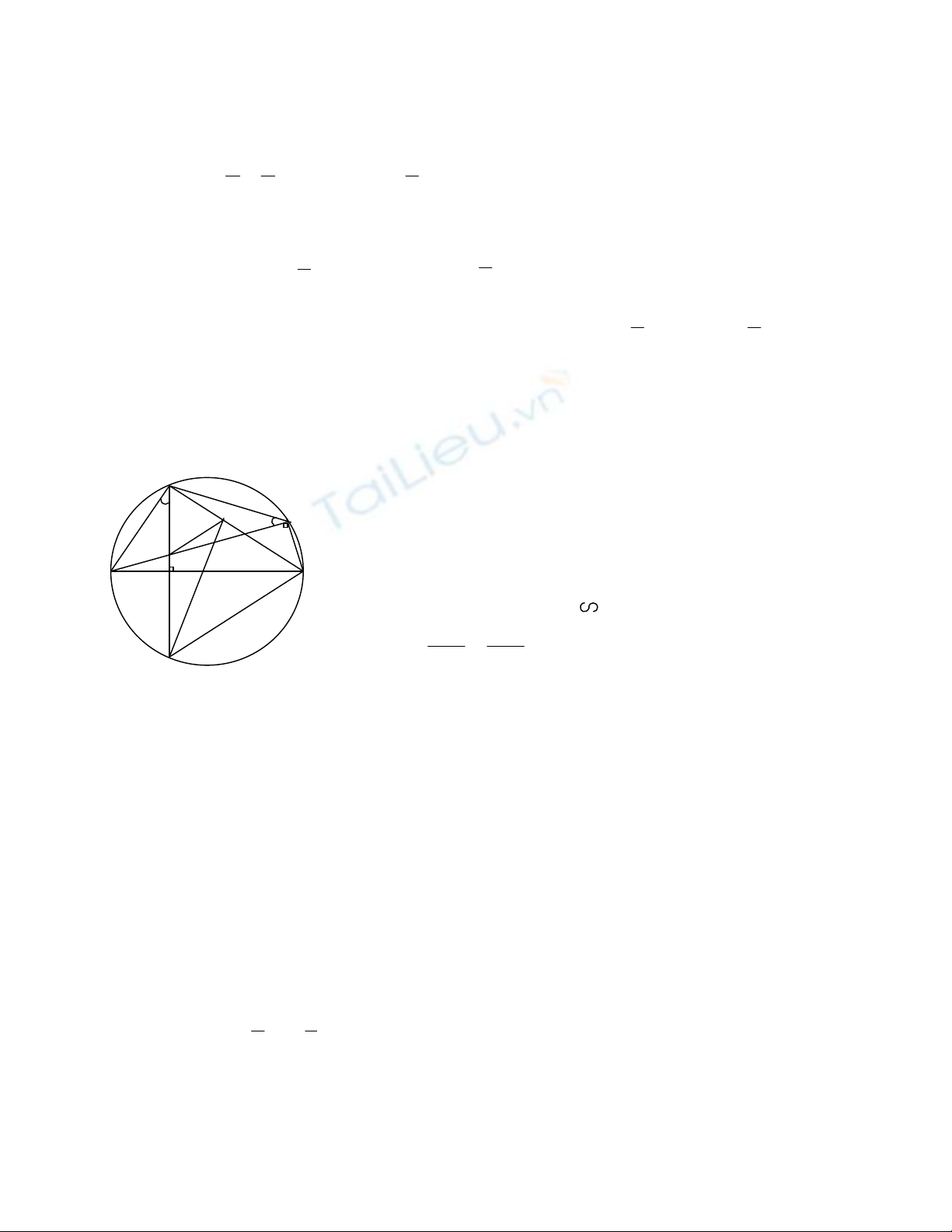
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho
AI =
2
3
AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc
cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.
a) Chứng minh tứ giác IECB nội tiếp được trong một đường tròn.
b) Chứng minh ∆AME ∆ACM và AM2 = AE.AC.
c) Chứng minh AE.AC - AI.IB = AI2.
d) Hãy xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đường
tròn ngoại tiếp tam giác CME là nhỏ nhất.
Bài 4. ( 1,5 điểm )
Người ta rót đầy nước vào một chiếc ly hình nón thì được 8 cm3. Sau đó người
ta rót nước từ ly ra để chiều cao mực nước chỉ còn lại một nửa. Hãy tính thể
tích lượng nước còn lại trong ly.
ĐÁP ÁN
ĐỀ SỐ 1.
Bài 1.
a)
Điều kiện a > 0 và a ≠ 1 (0,25đ)
a 1 1 2
K :
a 1 a 1
:
a( a 1) ( a 1)( a 1)
a 1 a 1
.( a 1)
a( a 1) a
b)
a = 3 + 2
2
= (1 +
2
)2
a 1 2
3 2 2 1 2(1 2)
K 2
1 2 1 2
c)
a 1 0
a 1
K 0 0
a 0
a
a 1
0 a 1
a 0
Bài 2.
a)
Khi m = 1 ta có hệ phương trình:
x y 1
x y
334
2 3
x y 1
3x 2y 2004
2x 2y 2
3x 2y 2004
x 2002
y 2001
b)
mx y 1 y mx 1
x y 3
334
y x 1002
2 3 2
y mx 1
y mx 1
3
3
m x 1001 (*)
mx 1 x 1002 2
2
Hệ phương trình vô nghiệm
(*) vô nghiệm
3 3
m 0 m
2 2
Bài 3.
a)
* Hình vẽ đúng
*
0
EIB 90
(giả thiết)
*
0
ECB 90
(góc nội tiếp chắn nửa đường tròn)
* Kết luận: Tứ giác IECB là tứ giác nội tiếp
b) (1 điểm) Ta có:
* sđ
cungAM
= sđ
cungAN
*
AME ACM
*GócAchung,suyra∆AME ∆ACM.
* Do đó: AC AM
AM AE
AM2 = AE.AC
c)
* MI là đường cao của tam giác vuông MAB nên MI2 = AI.IB
* Trừ từng vế của hệ thức ở câu b) với hệ thức trên
* Ta có: AE.AC - AI.IB = AM2 - MI2 = AI2.
d)
* Từ câu b) suy ra AM là tiếp tuyến của đường tròn ngoại tiếp tam giác CME.
Do đó tâm O1 của đường tròn ngoại tiếp tam giác CME nằm trên BM. Ta thấy
khoảng cách NO1 nhỏ nhất khi và chỉ khi NO1
BM.)
* Dựng hình chiếu vuông góc của N trên BM ta được O1. Điểm C là giao của
đường tròn đã cho với đường tròn tâm O1, bán kính O1M.
Bài 4. (2 điểm)
Phần nước còn lại tạo thành hình nón có chiều cao bằng một nửa chiều cao
của hình nón do 8cm3 nước ban đầu tạo thành. Do đó phần nước còn lại có thể
tích bằng
3
1 1
2 8
thể tích nước ban đầu. Vậy trong ly còn lại 1cm3 nước.
…………………………
A
B
M
E
C
I
O
1
N