SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH BÌNH PHƯỚC
KỲ THI TUYỂN SINH LỚP 10
NĂM HỌC: 2022 – 2023
ĐỀ THI MÔN: TOÁN (CHUYÊN )
ĐỀ CHÍNH THỨC
(Đề thi gồm có 01 trang)
Thời gian: 150 phút (không kể thời gian phát đề)
Ngày thi: 07/06/2022
Câu 1. (2,0 điểm) Cho biểu thức
2
23 1x xx x x
Px x x xx x
+ −+
=+−
−+
với
0, 1xx>≠
.
a) Rút gọn biểu thức
.P
b) Tìm giá trị nhỏ nhất của biểu thức
.P
Câu 2. (1,5 điểm) Cho phương trình
( )
( )
( )
2
1 2 01x x xm
− −+ =
với
là tham số. Tìm tất cả các
giá trị của tham số
m
để phương trình
( )
1
có đúng ba nghiệm phân biệt thỏa mãn
123
1111
3xxx
++=
.
Câu 3. (2,0 điểm)
a) Giải phương trình:
()()
2
1 3 64 4 6
x x xx
− − += − +
.
b) Giải hệ phương trình:
22
4 10 12 12 9 0
.
5
32 22
2
x xy x y y
x
y xy y
+ + − − +=
+
−− = − −
Câu 4. (2,5 điểm) Cho tam giác
ABC
nhọn nội tiếp đường tròn tâm
O
bán kính
R
. Gọi
H
là trực
tâm của tam giác
ABC
,
M
là điểm bất kì trên cung nhỏ
BC
. Gọi
,IJ
lần lượt là hình chiếu của
M
lên các đường thẳng
,.BC CA
Đường thẳng
IJ
cắt đường thẳng
AB
tại
K
.
a) Chứng minh bốn điểm
,, ,BKM I
cùng thuộc một đường tròn. Từ đó suy ra
.MK AB
⊥
b) Gọi
123
,,MM M
lần lượt là các điểm đối xứng của
M
qua các đường thẳng
,,.BC CA AB
Chứng minh bốn điểm
123
,,MM M
và
H
thẳng hàng.
c) Chứng minh khi điểm
M
di động trên cung nhỏ
BC
ta luôn có
23
4 .sin .M M R BAC
≤
Xác định vị trí của điểm
M
khi dấu bằng xảy ra.
Câu 5. (1,0 điểm)
a) Giải phương trình nghiệm nguyên:
22
6 2 7 0.x y xy y x− + + −−=
b) Cho
,xy
là các số nguyên thỏa mãn
22
2021 2022xy−+
chia hết cho
xy
. Chứng minh rằng
,xy
là các số lẻ và nguyên tố cùng nhau.
Câu 6. (1,0 điểm)
a) Cho
,ab
là các số thực dương thỏa mãn
2ab+=
.
Chứng minh:
22
1
11
ab
ba
+≥
++
.
b) Cho
,,abc
là các số thực dương thỏa mãn
16ab a b c++++=
.
Tìm giá trị lớn nhất của biểu thức
2 12 12 2
112
abc
Pabc
+++
=++
+++
.
………HẾT………
- Thí sinh không được sử dụng tài liệu.
- Giám thị coi thi không giải thích gì thêm.
1
SỞ GIÁO DỤC & ĐÀO TẠO
BÌNH PHƯỚC
ĐỀ CHÍNH THỨC
KÌ THI TUYỂN SINH LỚP 10 THPT
NĂM HỌC 2022 - 2023
ĐÁP ÁN – THANG ĐIỂM
Bài thi: TOÁN
(Đáp án – thang điểm gồm có 07 trang)
ĐÁP ÁN VÀ THANG ĐIỂM
Câu 1. (2 điểm)
Cho biểu thức
2
23 1x xx x x
Px x x xx x
+ −+
=+−
−+
với
0; 1xx>≠
Rút gọn biểu thức
()( )
()()()
( )
2
23 1
11 11
23
11
x xx x x
Px x x xx x
x x x xx x x
x
xxx xx
+ −+
=+−
−+
− ++ + −+
+
=+−
−+
0.5
23 1 1x xx xx
xx x
+ ++ −+
=+−
0.25
22 3
.
xx
x
++
=
0.25
Tìm giá trị nhỏ nhất của
P
33
2 2 22 . 2
Px x
xx
= + +≥ +
26 2= +
0.25
0.25
Vậy GTNN của
26 2P= +
khi và chỉ khi
33
22
xx
x
= ⇔=
(thỏa mãn điều kiện)
0.25
0.25
Câu 2. (1.5 điểm)
Nội dung
Điểm
Cho phương trình
( )
( )
( )
2
1 2 01x x xm− −+ =
với
m
là tham số. Tìm tất cả các giá trị của
tham số
m
để phương trình
( )
1
có đúng ba nghiệm phân biệt thỏa mãn
123
1111
3xxx
++=
.
2
Ta có:
( )
( )
( )
2
2
1
12 0 2 0*
x
x x xm x xm
=
− −+ =⇔
− +=
Để phương trình
( )
1
có ba nghiệm phân biệt
123
,,xxx
thì phương trình
()
*
phải có
hai nghiệm phân biệt khác 1.
0.25
0.25
( ) ( )
( )
2
'1 0 11
10 2 1
mmm
f fx x x m m
∆= − >
<
⇔ ⇔<

≠ =−+ ≠
0.25
Do vai trò các nghiệm như nhau, gọi
3
1x=
và phương trình
( )
*
có hai nghiệm
phân biệt
12
,xx
thỏa mãn hệ thức viet
12
12
2xx
xx m
+=
=
Từ yêu cầu bài toán:
123
1111
3xxx
++=
thì phương trình
( )
*
phải có nghiệm khác
0
hay
0m≠
0.25
0.125
12
1 2 3 12
1111 2 2 2 3
3 33
xx m
x x x xx m
+
+ + =⇔ =−⇔ =−⇔ =−
thỏa mãn điều kiện.
0.375
Câu 3. (2 điểm)
Nội dung
Điểm
a) Giải phương trình:
( )( )
2
1 3 64 4 6x x xx− − += − +
.
Phương trình đã cho
22
464 4630xx xx⇔−+− −++=
Đặt
2
4 60txx= − +≥
0.25
Phương trình trở thành:
2
4 30tt− +=
1
3
t
t
=
⇔=
0.25
Với
22 27
3 4 63 4 30 27
x
t xx xx
x
= +
=⇒ −+=⇔−−=⇔
= −
0.25
Với
( )
22
1 4 61 4 50t xx xx vn=⇒ −+=⇔−+=
.
0.25
b) Giải hệ phương trình:
22
4 10 12 12 9 0
.
5
32 22
2
x xy x y y
x
y xy y
+ + − − +=
+
−− = − −
3
ĐK:
5
2
3
x
y
≥−
≥
Ta có
() ( )
22
1 2 5 2 12 12 9 0
x yx y y⇔ + + − − +=
( )
2
'16 1 0
xy∆= + ≥
0.125
21
69
xy
xy
= −
⇒=−−
0.125
* Với
6 9 13xy=− − ≤−
loại.
0.125
* Với
21xy= −
thay vào phương trình
( )
2
ta được:
2
32 22 32y y yy−− += − −
( ) ( )( )
22 22 1 0
32 2
yyy
yy
−
⇔ − − +=
−+ +
0.25
( ) ( )
2
22 1 0 **
32 2
y
y
yy
=
⇔− +=
−+ +
0.125
+ Với
23
yx=⇒=
(thỏa mãn điều kiện).
0.125
+ Xét phương trình
()
**
:
()
22 1 **
32 2 y
yy
= +
−+ +
Vì
2
3
y≥
nên:
22
32 2 2 2 2
332 2
yy yy
−+ +≥ +> ⇒ <
−+ +
Mà
4
21 1 2
3
y+> +>
Vậy phương trình
( )
**
vô nghiệm.
Kết luận: hệ có nghiệm duy nhất
( ) ( )
; 3; 2xy =
.
0.125
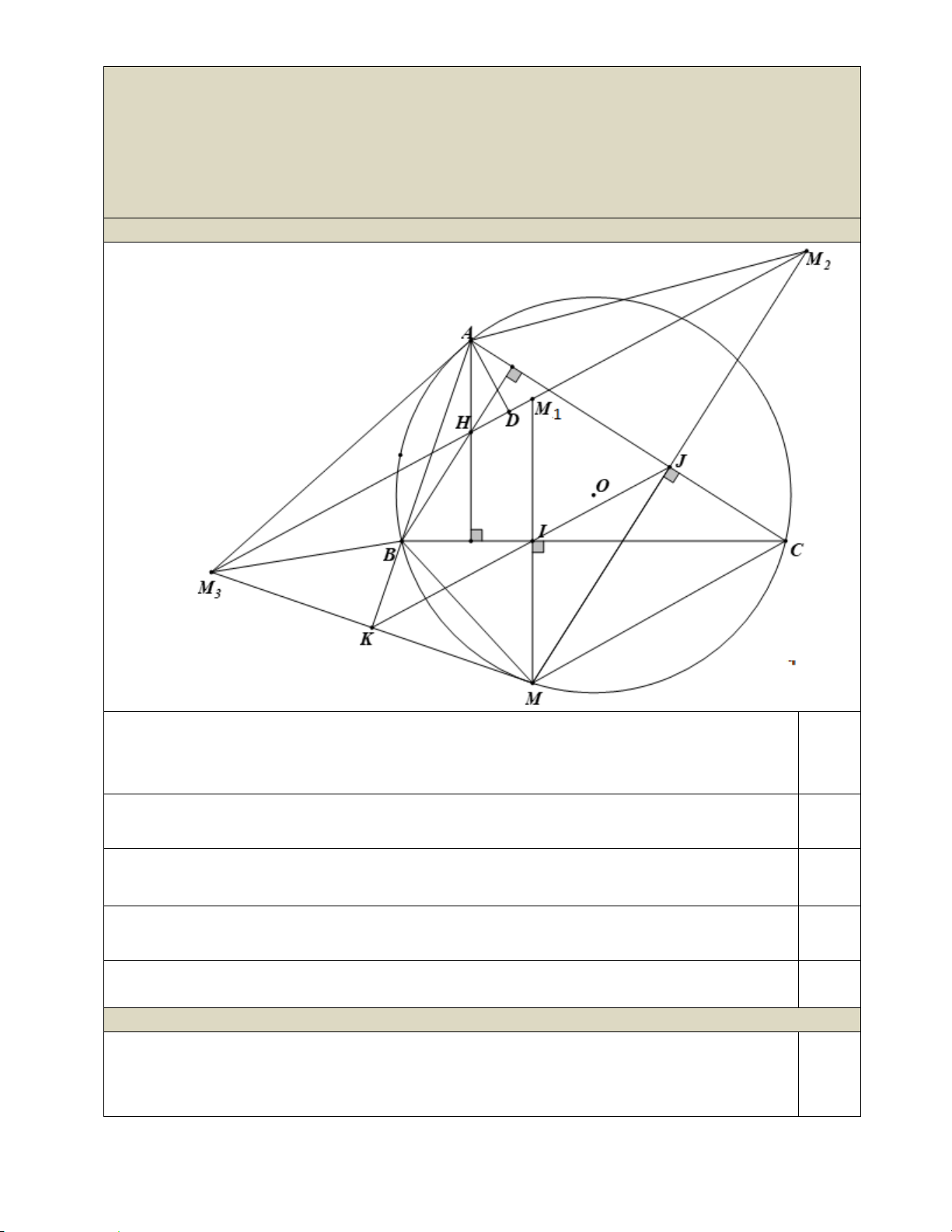
Câu 4. (2.5 điểm)
Nội dung
Điểm
Cho tam giác
ABC
nhọn nội tiếp đường tròn tâm
O
bán kính
R
. Gọi
H
là trực tâm của
tam giác
ABC
,
M
là điểm bất kì trên cung nhỏ
BC
. Gọi
,IJ
lần lượt là hình chiếu của
M
lên các đường thẳng
,.BC CA
Đường thẳng
IJ
cắt đường thẳng
AB
tại
K
.
a) Chứng minh bốn điểm
,, ,BKM I
cùng thuộc một đường tròn. Từ đó suy ra
.MK AB⊥
b) Gọi
123
,,MM M
lần lượt là các điểm đối xứng của
M
qua các đường thẳng
4
,,BC CA AB
. Chứng minh bốn điểm
123
,,MM M
và
H
cùng thuộc một đường
thẳng.
Chứng minh khi điểm
M
di động trên cung nhỏ
BC
ta luôn có
23
4 .sin .M M R BAC≤
Xác định vị trí của điểm
M
khi dấu bằng xảy ra.
a)
a) Ta có:
()
0
90MIC MJC gt= =
nên tứ giác
IJCM
nội tiếp
Do đó:
KIM JCM=
( trong bằng ngoài đỉnh đối)
0.125
0.125
Tứ giác
ABMC
nội tiếp nên
KBM ACM JCM= =
0.25
Từ đó suy ra
KIM KBM BIMK= ⇒
nội tiếp.
Vậy bốn điểm
,, ,BKM I
cùng thuộc một đường tròn.
0.25
Do
00
90 90BIM BKM MK AB=⇒ =⇒⊥
(đpcm)
0.25
Lưu ý: khi học sinh vẽ điểm M sao cho J nằm ngoài AC, K nằm trong AB vẫn đạt
điểm tối đa.
b)
Ta có
12 23
// , // .IJ M M JK M M
và theo giả thiết có
,,IJK
thẳng hàng nên ta có các điểm
123
,,MM M
thẳng hàng.
0.125
0.125