SỞ GIÁO DỤC VÀ ĐÀO TẠO
SƠN LA
-----------
ĐỀ THI CHÍNH THỨC
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2019 - 2020
MÔN THI: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
---------------------
Bài 1.(3,0 ñi5m)
a) Gii phương trình 3(x + 2) = x +36
b) Gii h' phương trình 4x 3 1
3 2
y
x y
− =
− + =
c) Rút g,n bi.u th0c
( )
2. 4
2 2
x
P x
x x
= + −
+ −
(v4i
0x≥
và
x 4≠
)
Bài 2.(1,5 ñi5m)
Trong kỳ thi tuy.n sinh vào l4p 10 năm h,c 2019 – 2020, sB thí sinh vào trưDng THPT chuyên bHng
2
3
sB thí
sinh thi vào trưDng PTDT NIi trú. BiKt rHng tLng sB phòng thi cNa c hai trưDng là 80 phòng thi và mQi phòng
thi có ñúng 24 thí sinh. HTi sB thí sinh vào mQi trưDng bHng bao nhiêu?
Bài 3. (1,5 ñi5m)
Cho parabol (P) 2 y x=và ñưDng thVng 2
2( 1) 2y m x m m= − + + (m là tham sB,
m∈ℝ
).
a) Xác ñYnh tZt c các giá trY cNa m ñ. ñưDng thVng (d) ñi qua ñi.m I (1; 3).
b) Tìm m ñ. parabol (P) c^t ñưDng thVng (d) t_i hai ñi.m phân bi't A, B. G,i 1 2
,x x là hoành ñI hai ñi.m
A, B; tìm m sao cho 2 2
1 2 1 2
x x 6 2020x x+ + =
.
Bài 4. (3,0 ñi5m)
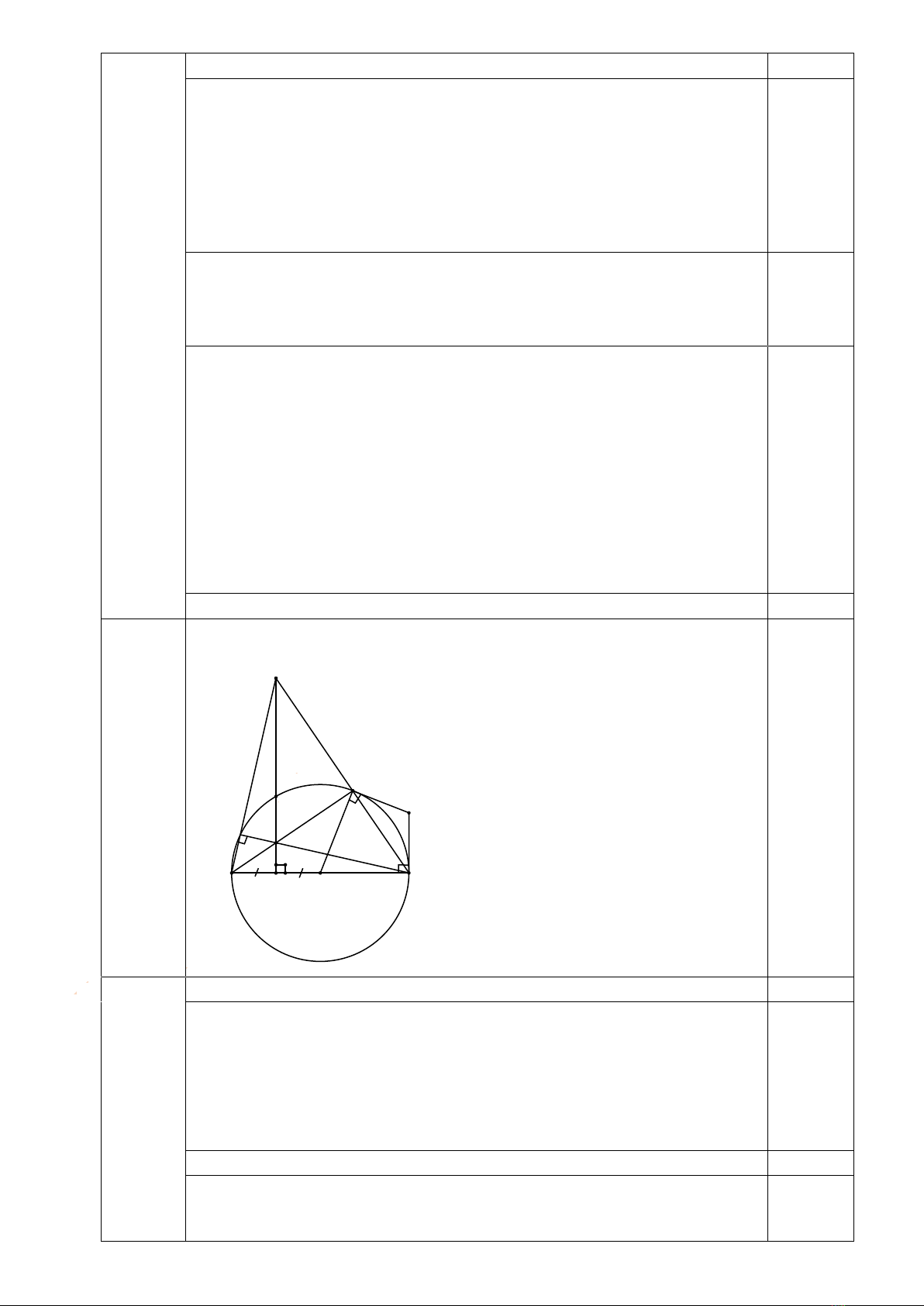
Cho ñưDng tròn (O) ñưDng kính AB = 2R và C là mIt ñi.m nHm trên ñưDng tròn sao cho CA > CB. G,i I là
trung ñi.m cNa OA, vb ñưDng thVng d vuông góc v4i AB t_i I, d c^t tia BC t_i M và c^t ño_n AC t_i P, AM
c^t ñưDng tròn (O) t_i ñi.m th0 hai K.
a) Ch0ng minh t0 giác BCPI nIi tiKp ñưfc trong mIt ñưDng tròn.
b) Ch0ng minh ba ñi.m B, P, K thVng hàng.
c) Các tiKp tuyKn t_i B và C cNa ñưDng tròn (O) c^t nhau t_i Q, biKt BC = R. Tính ñI dài BK và di'n tích t0
giác QAIM theo R.
Bài 5. (1,0 ñi5m)
Gii phương trình
3 3x x x− = +
HƯjNG DkN CHlM VÀ BImU ðImM
Bài ðáp án ði.m
Bài 1
a)(1,0 ñi5m)
3(x + 2) = x + 36
3x + 6 = x + 36 0,25
2x = 30
x = 15
0,25
0,25
Vpy phương trình ñã cho có 1 nghi'm x =15 0,25
b) (1,0 ñi5m)
4x 3 1
3 2
y
x y
− =
− + =
3x 3 x 1
3 2 1 3 2x y y
= =
⇔ ⇔
− + = − + =
0,5
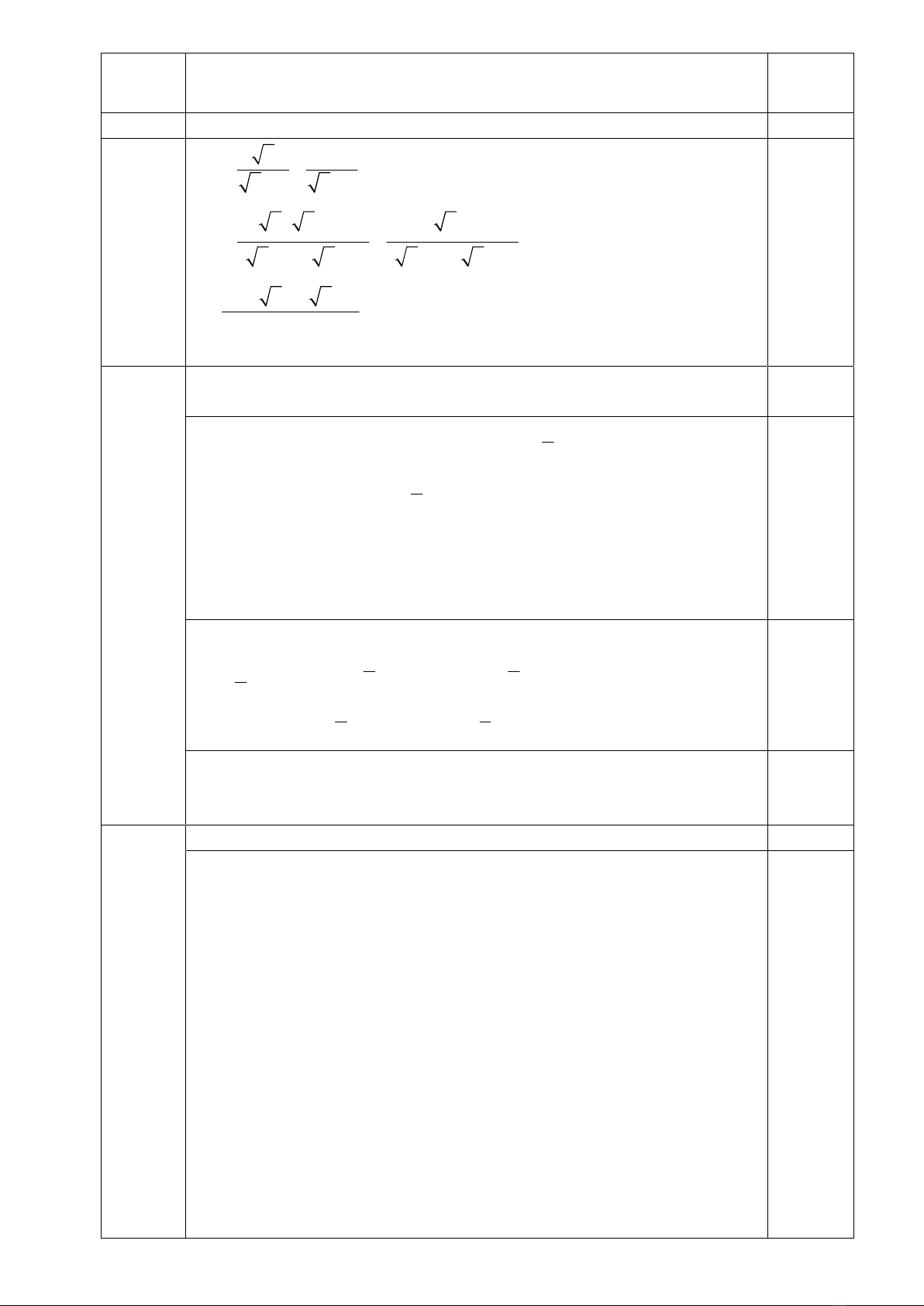
(3,0
ñi5m)
x 1 x 1
3 3 1
y y
= =
⇔ ⇔
= =
Vpy h' ñã cho có nghi'm duy nhZt
x 1
1
y
=
0,5
b) (1,0 ñi5m)
( )
2
. 4
2 2
x
P x
x x
= + −
+ −
(v4i
0
x
≥
và
x 4
≠
)
(
)
( )( )
(
)
( )( )
( )
( )
2 2 2
. 4
2 2 2 2
2 2 4 . 4
4
4
x x x
P x
x x x x
x x x x
x
x
− +
= + −
+ − + −
− + +
= −
−
= +
0,5
0,5
Bài 2
(1,5
ñi5m)
G,i sB thí sinh vào trưDng THPT Chuyên và sB thí sinh vào trưDng PTDT
NIi trú lrn lưft là x , y (thí sinh) (ñisu ki'n x > 0, y > 0)
0,25
Vì sB thí sinh vào trưDng THPT Chuyên bHng
2
3
sB thí sinh vào trưDng
PTDT NIi trú nên ta có:
2
3
x y
=
(1)
Vì tLng sB phòng thi cNa c hai trưDng là 80 phòng thi và mQi phòng thi có
ñúng 24 thí sinh nên tLng sB thí sinh cNa c hai trưDng là:
24.80 = 1920 (thí sinh)
Do ñó ta có phương trình; x + y = 1920 (2)
0,25
0,25
Tu (1) và (2) ta có h' phương trình
2 2
2
1152
3 3
3
2 5 768
1920 1920 1920
3 3
x y x y y
x y
x
x y y y y
= =
=
=
⇔ ⇔ ⇔
=
+ = + = =
0,25
ðBi chiKu ñisu ki'n ta thZy x = 768; y = 1152 ñsu thTa mãn.
Vpy sB thí sinh vào trưDng THPT Chuyên và sB thí sinh vào trưDng PTDT
NIi trú lrn lưft là 768 thí sinh , 1152 thí sinh.
0,25
0,25
Bài 3
(1,5
ñi5m)
3 a)(0,5 ñi5m)
ð. ñưDng thVng (d) 2
2( 1) 2
y m x m m
= − + + ñi qua ñi.m I (1;3) thì x = 1; y
= 3 thTa mãn phương trình ñưDng thVng (d) nên ta có:
2
2
2
3 2( 1).1 2
2 2 2 3
4 5 0
m m m
m m m
m m
= − + +
⇔ + + − =
⇔ + − =
( )( ) ( )
( )( )
21 4 4 0
1 1 4 1 0
1 5 0
1 0
5 0
1
5
m m
m m m
m m
m
m
m
m
⇔ − + − =
⇔ − + + − =
⇔ − + =
− =
⇔+ =
=
⇔= −
Vpy v4i m = 1 howc m = x 5 thì ñưDng thVng (d) ñi qua ñi.m I(1;3)
0,25
0,25
3 b) (1,0 ñi5m)
(P)
2
y x
=và (d)
2
2( 1) 2
y m x m m
= − + +
( 1)
m
≠
Hoành ñI giao ñi.m cNa (d) và (P) là nghi'm cNa phương trình:
2 2
2 2
2( 1) 2 (1)
2( 1) ( 2 ) 0
x m x m m
x m x m m
= − + +
⇔ − − − + =
' 2 2 2
( 1) 2 2 1 0
m m m m
= − + + = + >
v4i m,i m
0,25
Phương trình (1) luôn có hai nghi'm phân bi't v4i m,i m
Khi ñó theo h' th0c Vixét
(
)
1 2
2
1 2
2 1
(2)
( 2 )
x x m
x x m m
+ = −
= − +
Theo bài ra, ta có:
2 2
1 2 1 2
x x 6 2020
x x+ + =
(
)
( )
2
1 2 1 2 1 2
2
1 2 1 2
2 6 2020
4 2020(3)
x x x x x x
x x x x
⇔ + − + =
⇔ + + =
Thay (2) vào (3) ta có:
[
]
22
2 2
2( 1) 4( 2 ) 2020
4 4 4 4 8 2020
12 2016
168
m m m
m m m m
m
m
− − + =
⇔ − + − − =
⇔ = −
⇔ = −
0,25
Vpy m =
−
168 thTa mãn bài. 0,25
Bài 4
(3,5
ñi5m)
Vb hình ñúng cho câu a
0,25
4.1 a (0,75 ñi5m)
Xét (O) có
0
ACB 90
= (Góc nIi tiKp ch^n n{a ñưDng tròn) nên
0
PCB 90
=
Ta có:
d AB
⊥
t_i I;
P d
∈
nên
PI AB
⊥
t_i I =>
0
PIB 90
=
Xét t0 giác BCPI có:
0
PCB 90
= và
0
PIB 90
=(cmt)
Do ñó t0 giác BCPI nIi tiKp ñưfc ñưDng tròn.
0,25
0,25
0,25
4.1 b (1,0 ñi5m)
Xét
MAB
có
MI AB
⊥
t_i I(gt);
AC BM
⊥
t_i C (
0
ACB 90
=)
Mà
{
}
MI AC P
∩ ≡
nên P là tr|c tâm cNa
MAB
(1) 0,25
Q
P
K
P
M
I
B
O
A
C
L_i có:
0
AKB 90
= (Góc nIi tiKp ch^n n{a ñưDng tròn)
BK AK
⊥
t_i K hay
BK AM
⊥
t_i K
BK là ñưDng cao cNa
MAB
(2)
Tu (1) và (2) suy ra BK ñi qua P hay 3 ñi.m B, P, K thVng hàng.
0,25
0,25
0,25
4.1 c (1,0 ñi5m)
Có OA = R mà I là trung ñi.m cNa AO nên
O
2 2
OA R
AI I
= = =
BI = OB + IO =
3R
2 2
R
R+ =
Xét
BOC
có OB = OC = BC = R nên
BOC
là tam giác ñsu.
Do ñó
0
60
OBC =hay
0
60
ABC =
Xét
ABC
có :
0
ACB 90
= (Góc nIi tiKp ch^n n{a ñưDng tròn)
Nên
0
90
ABC CAB+ = mà
0
60
ABC =nên
0 0 0
90 60 30
CAB = − = hay
0
30
PAI =
Xét
0
: 90
AIP AIP = (
;
d AB P d
⊥ ∈
) nên:
0
R R 3 3
.tan .tan30 .
2 2 3 6
R
PI AI PAI= = = =
Xét
ABK
và
BI
P
có
ABK
chung;
0
90
AKB PIB= =
0,25
Do ñó
BI
ABK P
∼
(g.g)
BK BI
AK PI
⇒ =
(các c_nh tương 0ng t} l') hay
BK AK
BI PI
=
2 2
3R 3 9 1
3 3
2 2 4 12
6 6
BK AK BK AK BK AK
R
⇒ = ⇒ = ⇒ =
Do ñó:
2 2 2 2 2 2 2
4R 12R
9 1 9 1 7 7
7
4 12 4 12 3 3
BK AK BK AK AB+
= = = = =
+
Suy ra: BK =
189
7
R
(ñơn vY ñI dài)
0,25
Có
B
AIM AK
∼
(g.g)
MI BK
AI AK
⇒ =
(các c_nh tương 0ng t} l')
Mà
BK BI
AK PI
=
(cmt) nên
MI BI
AI PI
=
3R
.
. 3R 6 3 3
2 2 .
4 2
3. 3
6
R
AI BI R
MI PI R
⇒ = = = =
0,25
Tu Q k~
IM
QH
⊥
t_i H. D• dàng ch0ng minh ñưfc t0 giác QHIB là hình
vuông. Suy ra QH = BI
Ta có :
. .
.( )
2 2 2
AMQI AMI QMI
AI MI QH MI MI
S S S AI QH
= + = + = +
0,25
2
3 3 3 3
.( ) . .
2 2 2 2
MI AB R R
AI BI MI R= + = = =
(ñvdt)
Bài 5
(1,0
ñi5m)
3 3
x x x
− = +
ðisu ki'n
0 9
x
< ≤
0,25
Bình phương hai vK phương trình ñã cho, ta ñưfc:
2
3 2
3 .( 3 )
3. 3
x x x
x x x
− = +
⇔ + + =
0,25
2 3 3
3 2
3
3
1 1 1 1
3. . 3. . 3
3 3 3 3
1 10 10 3
9
3 3 3
1 10 3
9
3
x x x
x
x
⇔ + + + = +
⇔ + = =
⇔ + =
0,25
3
10 3 3
9 3
x⇔ = −
(thTa mãn ñisu ki'n)
Vpy phương trình ñã cho có 1 nghi'm
3
10 3 3
9 3
x= −
0,25