THI TH TRƯNG CHUYÊN ðHSP HÀ NI 2009  2010
=============================================
==============================================
1
TRƯNG ðHSP HÀ NI
ð THI TH ðI HC LN I NĂM 2010
TRƯNG THPT CHUYÊN – ðHSP Môn thi: TOÁN
Thi gian làm bài: 180 phút, không k$ thi gian giao ñ'
==========================================
Câu 1. ( 2,0 ñi$m )
Cho hàm s. y = 2x
3
+ 9mx
2
+ 12m
2
x + 1, trong ñó m là tham s..
1. Kh8o sát s: bi;n thiên và v> ñ? th@ cBa hàm s. ñã cho khi m = D 1.
2. Tìm tFt c8 các giá tr@ cBa m ñ$ hàm s. có c:c ñGi tGi x
Cð
, c:c ti$u tGi x
CT
thIa mãn:
x
2Cð
= x
CT
.
Câu 2. ( 2,0 ñi$m )
1. Gi8i phương trình: + + 1 = 4x
2
+ .
2. Gi8i phương trình: 5cos(2x +
π
) = 4sin(
π
D x) – 9 .
Câu 3. ( 2,0 ñi$m )
1. Tìm hO nguyên hàm cBa hàm s.: f(x) =

+
++
.
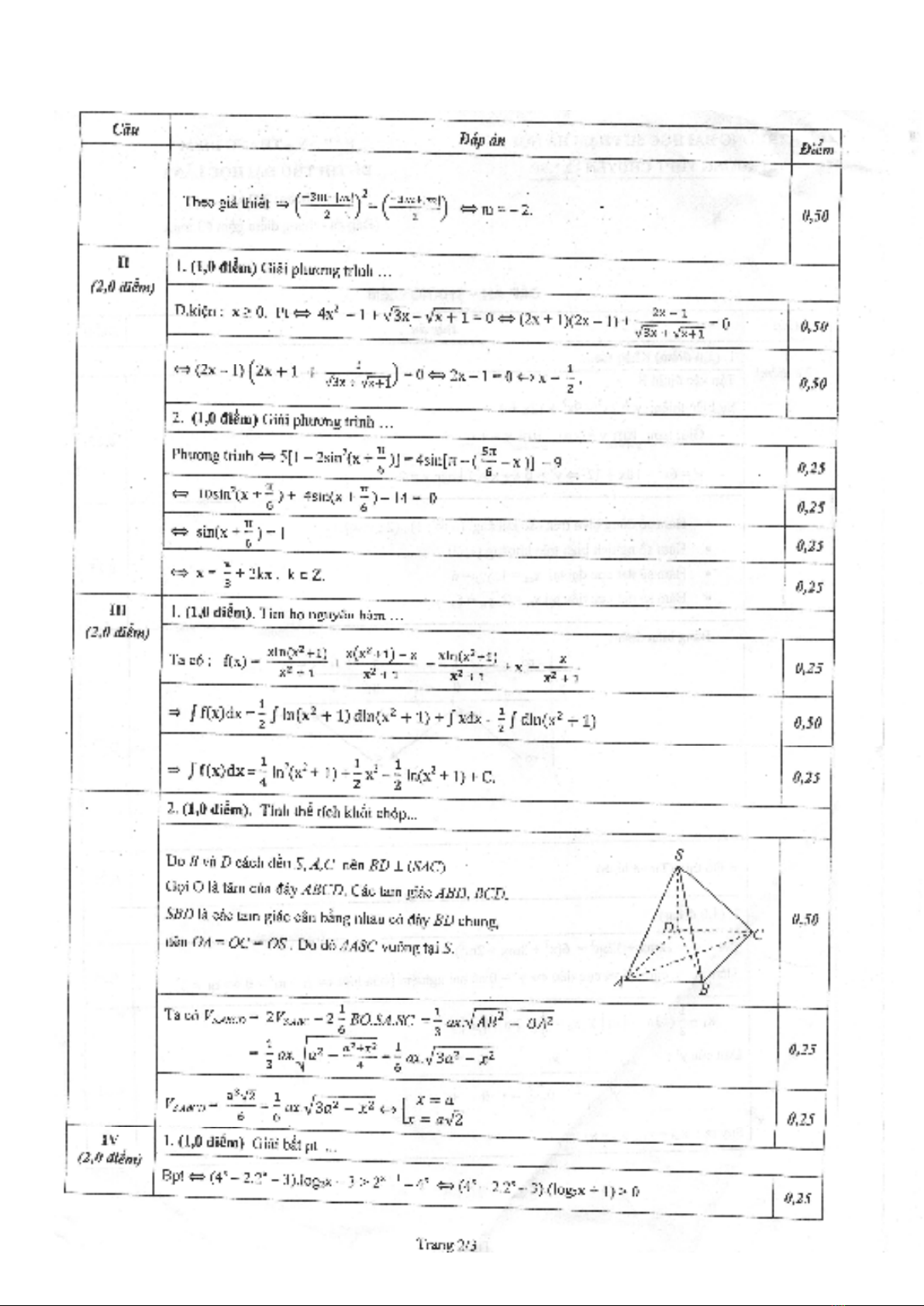
2. Cho hình chóp S.ABCD có SA =x và tFt c8 các cGnh còn lGi có ñU dài bWng a.
ChXng minh rWng ñưng thYng BD vuông góc vZi m[t phYng (SAC). Tìm x theo a
ñ$ th$ tích cBa kh.i chóp S.ABCD bWng
.
Câu 4. ( 2,0 ñi$m )
1. Gi8i bFt phương trình: (4
x
– 2.2
x
– 3). log
2
x – 3 >
+
D 4
x
.
2. Cho các s. th:c không âm a, b.ChXng minh rWng:
( a
2
+ b +
) ( b
2
+ a +
)
≥
( 2a +
) ( 2b +
).
Câu 5. ( 2,0 ñi$m )
Trong m[t phYng vZi h` tOa ñU Oxy, cho ba ñưng thYng :
d
1
: 2x + y – 3 = 0, d
2
: 3x + 4y + 5 = 0 và d
3
: 4x + 3y + 2 = 0.
1. Vi;t phương trình ñưng tròn có tâm thuUc d
1
và ti;p xúc vZi d
2
và d
3
.
2. Tìm tOa ñU ñi$m M thuUc d
1
và ñi$m N thuUc d
2
sao cho

+ 4

= .
………………………………..H;t…………………………………..
THI TH TRƯNG CHUYÊN ðHSP HÀ NI 2009  2010
=============================================
==============================================
2
THI TH TRƯNG CHUYÊN ðHSP HÀ NI 2009  2010
=============================================
==============================================
3
THI TH TRƯNG CHUYÊN ðHSP HÀ NI 2009  2010
=============================================
==============================================
4
THI TH TRƯNG CHUYÊN ðHSP HÀ NI 2009  2010
=============================================
==============================================
5
ƯNG ðHSP HÀ NI ð THI TH ðI HC LN II NĂM 2010
TRƯNG THPT CHUYÊN – ðHSP Môn thi: TOÁN
_______________
Thi gian làm bài: 180 phút, không k$ thi gian phát ñ'
==========================================
Ngày thi: 07 – 3 – 2010
.
Câu 1. ( 2,0 ñi$m). Cho hàm s. y =
−
−
.
1. Kh8o sát s: bi;n thiên và v> ñ? th@ ( C ) cBa hàm s..
2. Lep phương trình ti;p tuy;n cBa ñ? th@ ( C ) mà ti;p tuy;n này cft các trgc Ox , Oy
lhn lưit tGi các ñi$m A và B thIa mãn OA = 4OB.
Câu 2. ( 2,0 ñi$m)
1. Gi8i phương trình:



−
+
+ 2tan2x + cos2x = 0.
2. Gi8i h` phương trình:
=−++++
=−++++



Câu 3. ( 2,0 ñi$m)
1. Tính tích phân: I =
∫+
+

.
2. Cho lăng trg ñXng ABC.A’B’C’ có ñáy ABC là tam giác vuông vZi AB = BC = a,
cGnh bên A A’ = a
. M là ñi$m trên A A’ sao cho
 =
. Tính th$ tích cBa kh.i tX
di`n MA’BC’.
Câu 4. ( 2,0 ñi$m)
1. Tìm tFt c8 các giá tr@ cBa tham s. a ñ$ phương trình sau có nghi`m duy nhFt:
log
5
(25
x
– log
5
a ) = x.
2. Cho các s. th:c dương a, b, c thay ñli luôn thIa mãn a + b + c = 1.
ChXng minh rWng :
≥
+
+
+
+
+
+
+
+
Câu 5. ( 2,0 ñi$m).
Trong m[t phYng vZi h` tOa ñU Oxy, cho ñi$m E(D1;0) và ñưng tròn
( C ): x
2
+ y
2
– 8x – 4y – 16 = 0.
1. Vi;t phương trình ñưng thYng ñi qua ñi$m E cft ( C ) theo dây cung MN có ñU dài
ngfn nhFt.
2. Cho tam giác ABC cân tGi A, bi;t phương trình ñưng thYng AB, BC lhn lưit là:
x + 2y – 5 = 0 và 3x – y + 7 = 0. Vi;t phương trình ñưng thYng AC, bi;t rWng AC ñi
qua ñi$m F(1; D 3).
DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD H;tDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD
D kin thi th ln sau vào các ngày 27,28 tháng 3 năm 2010.