
[CTCT] - CHÚNG TA CÙNG TIẾN
Trang 1
GIẢI ĐỀ THI THỬ [CTCT] – VẬT LÝ
Câu 1. Một chất điểm đang chuyển động theo chiều dương của trục 𝑂𝑥. Tại thời điểm 𝑡1, vật
đi qua gốc tọa độ với vận tốc 𝑣0. Tại thời điểm 𝑡2=𝑡1+1, vật có vận tốc 𝑣0−𝑎. Tại thời
điểm 𝑡3=𝑡2+1, vật có vận tốc 𝑣0−2𝑎 (𝑣0>2𝑎>0) và vẫn chưa đổi chiều chuyển
động. Kết luận nào sau đây đúng :
A. Vật chuyển động chậm dần theo chiều dương sau đó dừng lại.
B. Vật chuyển động thẳng biến đổi đều.
C. Vật chuyển động thẳng đều.
D. Vật sẽ tiếp tục chuyển động thêm môt đoạn theo chiều dương
Giải.
Câu này có độ lừa đảo khá là cao ! Nhiều bạn đọc đề rồi nhận xét là do cứ sau 1s, vận tốc
chất điểm giảm 𝑎, nên vật đang chuyển động biến đổi đều (chậm dần). Sai rồi ! Dựa vào dữ
kiện bài toán, chúng ta chỉ khẳng định được là gia tốc TRUNG BÌNH của chất điểm trong
hai giai đoạn (𝑡1→𝑡2,𝑡2→𝑡3) là bằng nhau thôi ! Còn muốn khẳng định tính chât chuyển
động của vật là biến đổi đều hay không chúng ta phải dựa vào gia tốc TỨC THỜI nhé !
Suy ra B, C sai từ vòng gửi xe ! (do có chữ “đều”)...
Còn A thì sao ? Sai luôn. Ta chỉ biết là vận tốc của chất điểm tại 𝑡2 bé hơn tại 𝑡1, tại 𝑡3 bé
hơn tại 𝑡2. Nhưng không thể khẳng định được là vận tốc chất điểm chậm dần từ 𝑡1 đến 𝑡2. Có
thể có một giai đoạn nào đó nó tăng, rồi sau đó giảm lại thì sao. Miễn sao, tại 𝑡2 và 𝑡3 vận tốc
vận tốc là 𝑣0−𝑎 và 𝑣0−2𝑎 !!!!
Chỉ còn lại thằng D thôi. Vận tốc nó theo chiều dương 𝑂𝑥, tại cuối thời điểm 𝑡3 vẫn lớn hơn
0 (𝑣0−2𝑎>), và cũng chưa đổi chiều chuyển động nên chất điểm sẽ tiếp tục chuyển động
thêm một đoạn nữa theo chiều dương.
⇒ Chọn D
Câu 2. Một vật đựơc ném từ mặt đất với vận tốc có độ lớn 𝑣0 theo phương hợp với mặt đất
một góc 𝛼 (0<𝛼<900) Biết vận tốc của vật tại thời điểm ném và lúc vật cham đất hợp với
nhau một góc 60𝑜. Bỏ qua mọi lực cản. Tính vận tốc của vật khi vật có gia tốc tiếp tuyến nhỏ
nhất ?
C. 1
2𝑣0. B. 𝑣0. C. 0. D. √3
2𝑣0.
Giải.
Do tính đối xứng của quỹ đạo ném xiên (hình parabol), nên vân tốc khi chạm đất bằng vận
tốc tại thời điểm ném và..... So với phương ngang, góc hợp bởi vận tốc tại thời điểm ném và
lúc vật chậm đất sẽ bằng nhau về độ lớn. Vận tốc lúc ném có chiều hướng lên, lúc chạm đất
.
Group
: .
[CTCT] - CHÚNG TA CÙNG TIẾN
Trang 2
có chiều hướng xuống. Tức là góc hơp bởi vận tốc tại thời điểm và lúc chạm đất là 2𝛼=
600→𝛼=30𝑜.
Gia tốc tiếp tuyến nhỏ nhất lúc vật đạt độ cao cực đại. Tại độ cao cực đại, thành phần vận
tốc theo phương thẳng đứng bằng 0. Vân tốc bằng vận tốc theo phương ngang : 𝑣=𝑣𝑥=
𝑣0𝑥=𝑣0𝑐𝑜𝑠𝛼=√3
2𝑣0
⇒ Chọn D
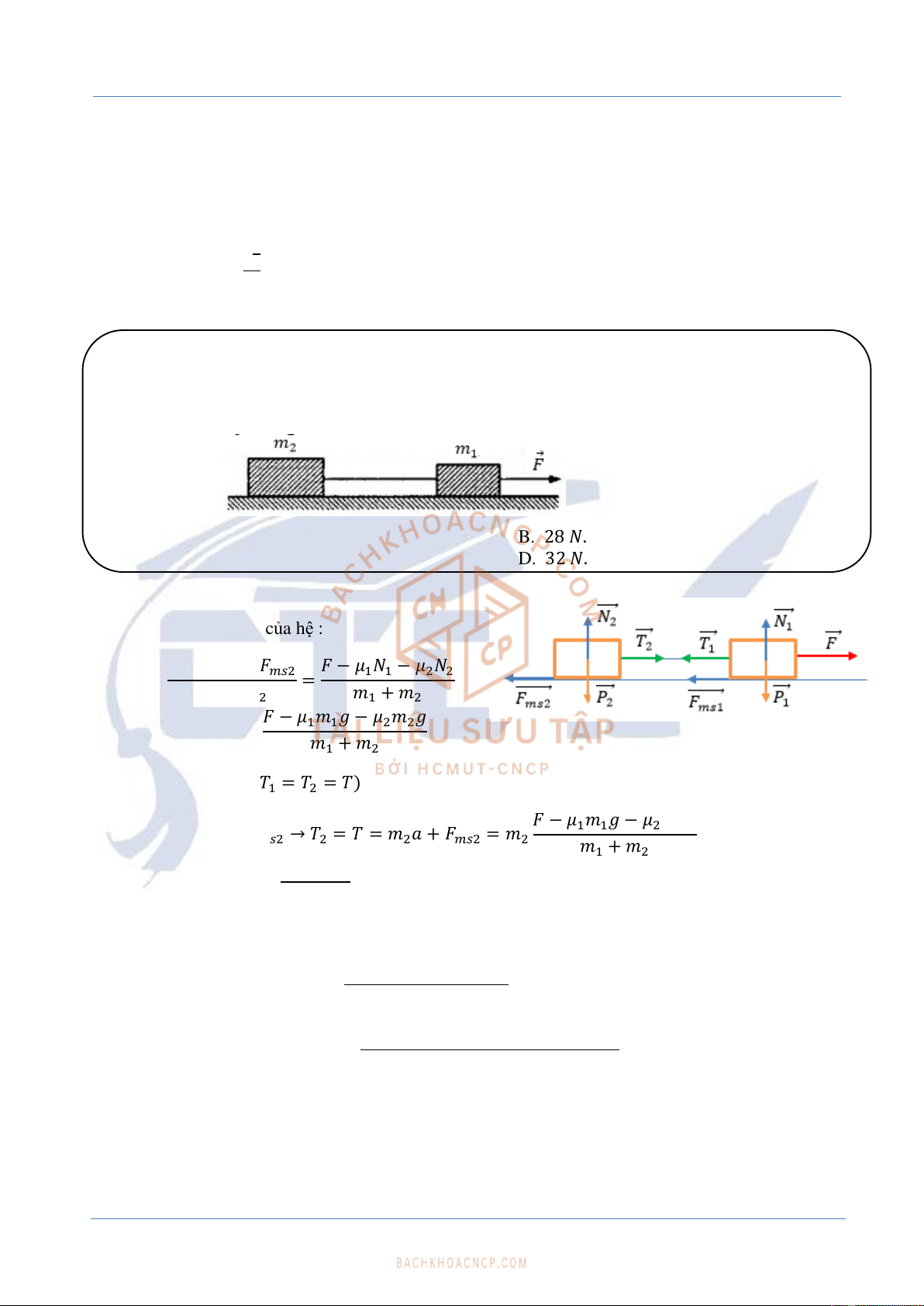
Câu 3. Cho hệ như hình vẽ. Biết 2𝑚1=3𝑚2=6 𝑘𝑔. Hệ sô ma sát trượt giữa 𝑚1,𝑚2 với
mặt phẳng lần lượt là 𝜇1,𝜇2 với 𝜇1=2𝜇2=0.2. Lực căng tối đa dây có thể chịu được là
𝑇0=10 𝑁. Tìm độ lớn cực đại của lực 𝐹 để dây không bị đứt ? Cho 𝑔=10 𝑚/𝑠2.
A. 24 𝑁. B. 28 𝑁.
C. 30 𝑁. D. 32 𝑁.
Giải.
Xét toàn hệ. Gia tốc của hệ :
𝑎=𝐹−𝐹𝑚𝑠1−𝐹𝑚𝑠2
𝑚1=𝑚2=𝐹−𝜇1𝑁1−𝜇2𝑁2
𝑚1+𝑚2
=𝐹−𝜇1𝑚1𝑔−𝜇2𝑚2𝑔
𝑚1+𝑚2
Xét riêng vật 𝑚2 : (𝑇1=𝑇2=𝑇)
𝑚2𝑎=𝑇2−𝐹𝑚𝑠2→𝑇2=𝑇=𝑚2𝑎+𝐹𝑚𝑠2=𝑚2𝐹−𝜇1𝑚1𝑔−𝜇2𝑚2𝑔
𝑚1+𝑚2+𝜇2𝑚2𝑔
=𝑚2
𝑚1+𝑚2(𝐹−(𝜇1−𝜇2)𝑚1𝑔)
Để dây không bị đứt : 𝑇≤𝑇0
→𝑚2𝐹−𝜇1𝑚1𝑔−𝜇2𝑚2𝑔
𝑚1+𝑚2+𝜇2𝑚2𝑔≤𝑇0
→𝐹≤(𝑚1+𝑚2)𝑇0+𝑚1𝑚2(𝜇1−𝜇2)𝑔
𝑚2
Thế số : 𝐹≤28 (𝑁)
⇒ Chọn D
.
Group
: .

[CTCT] - CHÚNG TA CÙNG TIẾN
Trang 3
Câu 4. Một chất điểm chuyển động thẳng với gia tốc không đổi 𝑎<0. Kết luận đúng là:
A. Chất điểm chuyển động chậm dần đều
B. Chất điểm chuyển động nhanh dần đều
C. Chất điểm chuyển động biến đổi đều.
D. Không thể kết luận được.
Giải.
Chất điểm chuyển động nhanh dần hay chậm dần, không chỉ phụ thuộc vào dấu của gia tốc
mà còn phụ thuộc vào chiều chuyển động : Cùng hay ngược chiều dương tọa độ ???
Nếu chất điểm chuyển động theo chiều dương tọa độ : 𝑎>0 chất điểm chuyển động nhanh
dần, 𝑎<0 chất điểm chuyển động chậm dần.
Nếu chất điểm chuyển động theo chiều âm tọa độ : 𝑎>0 chất điểm chuyển động chậm dần,
𝑎<0 chất điểm chuyển động nhanh dần.
Bởi vậy loại câu A, B.
Chất điểm chuyển động với gia tốc không đổi → chuyển động biến đổi đều.
⇒ Chọn C
Câu 5. Hạt chuyển động dưới lực 𝐹=(2𝑥𝑦+1)𝑖+𝑥2𝑗
(𝑁). Đơn vị 𝑥,𝑦 là mét (𝑚), Xác
định công của lực tác dụng khi hạt chuyển động từ điểm 𝐴(0,0) (𝑚) đến điểm 𝐵(1,1) (𝑚) ?
A. 2 𝐽. B. 4 𝐽.
C. 6 𝐽. D. 8 𝐽.
Giải.
Bài này là một bài toán liên quan đến lực thế. Vậy đặt ra câu hỏi “Thế nào lực thế ?” – Lực
thế là lực mà công tác dụng bởi lực không phụ thuộc vào quỹ đạo, chỉ phụ thuộc vào điểm
đầu và điểm cuối.
Với lực có dạng : 𝐹=𝐹𝑥𝑖+𝐹𝑦𝑗
. Lực 𝐹 được gọi là lực thế khi thỏa mãn :
𝜕𝐹𝑦
𝜕𝑥=𝜕𝐹𝑥
𝜕𝑦
Kí hiệu 𝜕
𝜕𝑥, 𝜕
𝜕𝑦 trên được gọi là đạo hàm riêng phần (từng phần) nhé ! Các bạn có thể lên mạng
tìm hiểu về cách tính. Cũng dễ thôi ^^ . Cái công thức đóng khung ở trên là để xác định xem
lực 𝐹 đã cho có phải là lực thế không. Nhưng khi đi thi, nếu đề bài cho một lực phụ thuộc vào
tọa độ như trên thì...... 99% LÀ LỰC THẾ nhé. 1% còn lại là do bạn quá XUI thôi. Nếu
nhớ, biết cách triển khai công thức đóng khung trên thì làm, không thì tự cho là lực thế luôn
:v :v
Cách tính công lực thế ? Công thức là thế này :
.
Group
: .

[CTCT] - CHÚNG TA CÙNG TIẾN
Trang 4
𝐴=∫𝐹.𝑑𝑠=∫(𝐹𝑥𝑖+𝐹𝑦𝑗
).(𝑑𝑥𝑖+𝑑𝑦𝑗)=∫(𝐹𝑥𝑑𝑥+𝐹𝑦𝑑𝑦)=∫𝐹𝑥𝑑𝑥+∫𝐹𝑦𝑑𝑦
Quay lại bài toán của chúng ta.
Ta có : 𝐹=𝐹𝑥𝑖+𝐹𝑦𝑗
=(2𝑥𝑦+1)𝑖+𝑥2𝑗
𝜕𝐹𝑦
𝜕𝑥=𝜕𝐹𝑥
𝜕𝑦=2𝑥 (∗)
Làm sao có kết quả (*) trên thì hỏi chị Google đi nhé.
Công của lực thế không phụ thuộc vào quãng đường đi, nên bạn có thể chọn quỹ đạo bất kỳ
cho nó !!!! Chọn sao cho tính toán dễ nhất nhé !
Chọn quỹ đạo chất điểm là các đường thẳng vuông góc với các trục
tọa độ. Từ A(0,0), chất điểm chuyển động thẳng với vị trí C(1,0).
Sau đó từ C(1,0), chuyển động thằng đến B(1,1).
Ta có : 𝐴𝐴𝐵=𝐴𝐴𝐶+𝐴𝐶𝐵
(1). Công trên đoạn AC :
𝐴𝐴𝐶=∫𝐹𝑥𝑑𝑥
𝐶
𝐴+∫𝐹𝑦𝑑𝑦
𝐶
𝐴
Trên đoạn AC : 𝑦=0=𝑐𝑜𝑛𝑠𝑡→𝑑𝑦=0
→𝐴𝐴𝐶=∫𝐹𝑥𝑑𝑥
𝐶
𝐴=∫(2𝑥.0+1)𝑑𝑥
𝐶
𝐴= ∫ 𝑑𝑥
𝑥=1
𝑥=0 =1(𝐽)
(1). Công trên đoạn CB :
𝐴𝐴𝐶=∫𝐹𝑥𝑑𝑥
𝐵
𝐶+∫𝐹𝑦𝑑𝑦
𝐵
𝐶
Trên đoạn AC : 𝑥=1=𝑐𝑜𝑛𝑠𝑡→𝑑𝑥=0
→𝐴𝐴𝐶=∫𝐹𝑦𝑑𝑦
𝐵
𝐶=∫(12)𝑑𝑦
𝐵
𝐶= ∫ 𝑑𝑦
𝑦=1
𝑦=0 =1(𝐽)
Vậy : 𝐴𝐴𝐵=𝐴𝐴𝐶+𝐴𝐶𝐵=2(𝐽)
⇒ Chọn A
.
Group
: .

[CTCT] - CHÚNG TA CÙNG TIẾN
Trang 5
Câu 6. Cho cơ hệ như hình vẽ. Vật 𝐴 có khối
lượng 𝑚1=1.5 𝑘𝑔, được đặt trên sàn. Vật
𝐵 khối lượng 𝑚2=0.45 𝑘𝑔, được buộc vào
sợi dây treo trên một thanh đòn nhẹ. Chiều
dài hai cánh tay đòn 𝑙1=0.6 𝑚,𝑙2=1 𝑚.
Cần đưa dây treo B nghiêng góc 𝛼 so với
phương thẳng đứng nhỏ nhất bao nhiêu để
sau khi buông tay, vật 𝐴 có thể nhấc khỏi
bàn.
A. 45𝑜. B. 60𝑜.
C. 65𝑜. D. 56𝑜.
Giải.
Gọi góc lệch ban đầu là 𝛼0. Xét tại thời điểm phương sợi dây hợp với phương ngang góc 𝛼.
Tại vị trí 𝛼, vật B có vận tốc là 𝑣. Bảo toàn năng lượng :
𝑚2𝑔𝑙(𝑐𝑜𝑠𝛼−𝑐𝑜𝑠𝛼0)=1
2𝑚2𝑣2 (1)
Lực căng dây T. Phương trình động lực học :
𝑇−𝑚2𝑔𝑐𝑜𝑠𝛼=𝑚2𝑣2
𝑙 (2)
(1),(2)→𝑇=𝑚2𝑔(3𝑐𝑜𝑠𝛼−2𝑐𝑜𝑠𝛼0)
Để vật A nhắc lên khỏi mặt đất thì momen lực căng dây T phải lớn hơn (hoặc bằng) momen
trọng lực 𝑃1 đối cới trục quay qua O.
𝑇𝑙2𝑐𝑜𝑠𝛼≥𝑚1𝑔𝑙1→𝑚2𝑔(3𝑐𝑜𝑠𝛼−2𝑐𝑜𝑠𝛼0)𝑙2𝑐𝑜𝑠𝛼≥𝑚1𝑔𝑙1
→𝑐𝑜𝑠𝛼0≤3
2𝑐𝑜𝑠𝛼− 𝑚1𝑙1
2𝑚2𝑙2𝑐𝑜𝑠𝛼≤3
2−𝑚1𝑙1
2𝑚2𝑙2=1
2→𝛼0≥60𝑜
⇒ Chọn B
Câu 7. Một chất điểm chuyển động có vận tốc 𝑣=𝑎𝑦𝑖+𝑏𝑐𝑜𝑠(𝑐𝑡)𝑗, với 𝑎,𝑏,𝑐 là hằng số.
Quỹ đạo của chất điểm có dạng :
A. Elip. B. Tròn.
D. Hyperbol. D. Đáp án khác.
Giải.
{𝑣𝑥=𝑎𝑦
𝑣𝑦=𝑏𝑐𝑜𝑠(𝑐𝑡)→{𝑣𝑥=𝑎(𝑏𝑐𝑠𝑖𝑛(𝑐𝑡)+𝐶1)=𝑎𝑏
𝑐sin(𝑐𝑡)+𝑐𝐶1
𝑦=𝑏𝑐𝑠𝑖𝑛(𝑐𝑡)+𝐶1
.
Group
: .


























