zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Điện - Điện tử

Giáo trình Cơ sở kỹ thuật điện - Mạch tuyến tính có nguồn chu kỳ không điều hòa

Chia sẻ: Thiên Nam Hải | Ngày: | Loại File: PDF | Số trang:6

Báo xấu

389
lượt xem 136
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu tham khảo chuyên ngành kỹ thuật công nghệ, điện và điện tử - Giáo trình Cơ sở kỹ thuật điện - Mạch tuyến tính có nguồn chu kỳ không điều hòa

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giáo trình Cơ sở kỹ thuật điện - Mạch tuyến tính có nguồn chu kỳ không điều hòa

Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 66 CHÆÅNG 5 MAÛCH TUYÃÚN TÊNH COÏ NGUÄÖN CHU KYÌ KHÄNG ÂIÃÖU HOÌA Trong thæûc tãú ngoaìi kêch thêch âiãöu hoìa ta thæåìng gàûp caïc kêch thêch chu kyì khäng âiãöu hoìa nhæ caïc nguäön chènh læu, nguäön xung chu kyì, caïc nguäön tên hiãûu âiãöu biãn duìng trong VTÂ cuîng nhæ trong KTÂ, nãn cáön dáùn ra phæång phaïp tênh maûch naìy åí chãú âäü xaïc láûp, laìm roî tênh læûa choün cuía phaín æïng maûch âäúi våïi táön säú, tæì âoï âæa âãún khaïi niãûm vãö phäø laì mäüt caïch biãøu diãùn tên hiãûu . Phán têch kêch thêch chu kyì khäng âiãöu hoaì thaình täøng caïc haìm âiãöu hoìa coï caïc táön säú khaïc nhau Theo toaïn hoüc : Báút kyì mäüt haìm chu kyì naìo thoía maîn âiãöu kiãûn Diricle âãöu coï thãø biãøu diãùn dæåïi daûng chuäùi vä haûn cuía caïc haìm læåüng giaïc (âiãöu hoìa, chuäùi Fourier) ∞ ƒ(t) = ƒ(t + T) = Ao + ∑C 1 km cos(kω.t + ψ k ) . (5-1) trong âoï : Ao thaình pháön hàòng ( ω = 0, ƒ = 0, T = ∞ ) k : säú thæï tæû cuía caïc âiãöu hoìa, Ckm, ψk : Biãn âäü vaì goïc pha âáöu cuía âiãöu hoìa thæï k. Nhæ váûy mäüt haìm chu kyì khäng hçnh sin chênh laì täøng cuía caïc âæåìng hçnh sin coï táön säú bäüi fk = k.f1 vaì goïc pha âáöu ψk .Våïi f1 =1/ T laì táön säú cå baín (táön säú cuía soïng báûc nháút). Vç mäùi âiãöu hoìa âãöu coï biãn âäü vaì pha ban âáöu cuía noï nãn chuäùi noïi trãn (5-1) coï thãø dæåïi daûng täøng caïc âæåìng sin vaì cos, mäùi âæåìng âãöu coï pha ban âáöu bàòng 0. ∞ ∞ ƒ(t) = A0 + ∑ Akm cos kω.t + ∑ Bkm sin kω.t (5-2) k =1 k =1 B km våïi Ckm = A 2 + B 2 ψk = arctg km km A km Thaình pháön hàòng A0 laì trë säú trung bçnh cuía haìm trong mäüt chu kyì táön säú cå baín : 1 T 2 T A0= ∫ ƒ(t) .dt (5-3) Akm= ∫ ƒ(t) cos kωt.dt (5-4) T 0 T 0 2 T Bkm= ∫ ƒ(t) sin kωt.dt (5-5) T 0 Trong caïc cäng thæïc trãn, k coï giaï trë nguyãn dæång chaûy tæì 1 âãún ∞. Khi chuäùi häüi tuû, nhæîng thaình pháön âiãöu hoìa cao phaíi nhoí dáön. Do âoï mäüt caïch gáön âuïng chè láúy mäüt vaìi säú haûn âáöu thæåìng cuîng âuí thoía maîn âäü chênh xaïc yãu cáöu. Nãúu goüi mäùi âæåìng hçnh sin æïng våïi mäùi âiãöu hoìa thæï k laì mäüt soïng thç táûp håüp caïc soïng taûo nãn haìm chu kyì khäng âiãöu hoìa. Soïng æïng våïi k =1, táön säú f1 våïi ω1 =2πf1 goüi laì soïng cå baín. Soïng æïng våïi k = 2 , f2 = 2f1 våïi ω2 = 2ω1 goüi laì soïng bäüi 2. Soïng æïng våïi k = 3 , f3 = 3f1 våïi ω3 = 3ω1 goüi laì soïng bäüi 3. Tæì soïng bäüi 2 tråí lãn goüi laì soïng báûc cao. Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
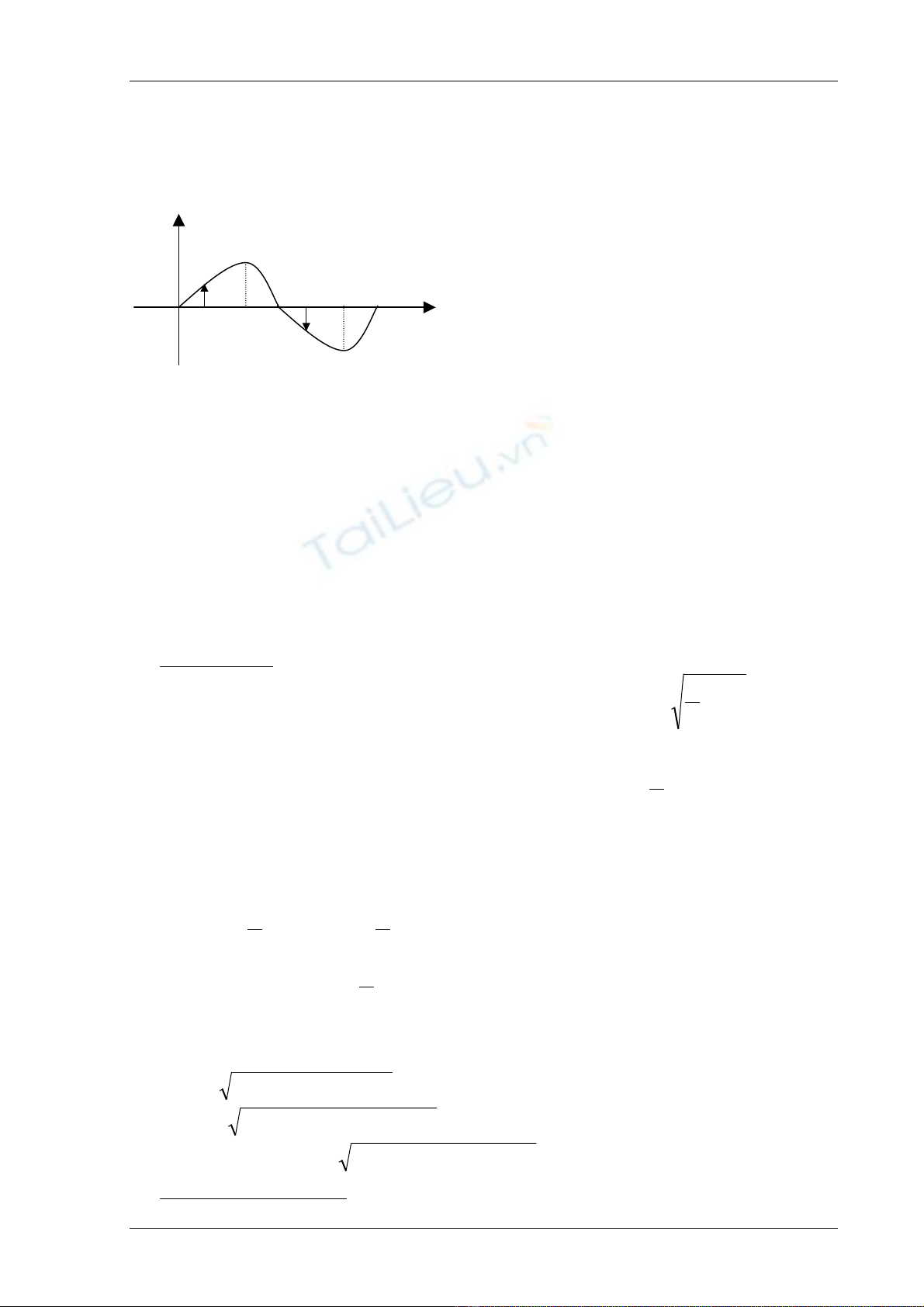
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 67 Trong thæûc tãú thæåìng gàûp caïc tên hiãûu chu kyì âäúi xæïng våïi truûc thåìi gian nhæ hçnh (h.5-1) tæïc laì nhæîng tên hiãûu coï âäü låïn taûi thåìi âiãøm ωt bàòng âäü låïn taûi thåìi âiãøm ωt +π nhæng traïi dáúu : f(ωt ) = -f(ωt +π) (5-6) Luïc naìy chuäùi Fourier khäng coï nhæîng thaình e pháön âiãöu hoìa chàôn, tæïc seî triãût tiãu åí caïc âiãøm 2k. Vç nãúu täön taûi nhæîng thaình pháön π e(ωt+π) 2π t âiãöu hoìa chàôn 2k ta seî coï : 0 e(ωt) T/2 T ωt ƒ2k(ωt + π) = A2kmcos[2k(ωt + π) + ψ2k] = h.5-1 A2km cos[2kωt + ψ2k] = ƒ2k(ωt) âiãöu naìy traïi våïi (5-6) Vç váûy âäúi våïi tên hiãûu chu kyì âäúi xæïng qua truûc thåìi gian ta phán têch Fourier ra caïc soïng cå baín + soïng báûc 3 + soïng báûc 5 + ...(noïi chung laì soïng báûc leí). Trong âoï ngoaìi soïng cå baín räöi âãún soïng bäüi 3 coï biãn âäü âaïng kãø. Tháût váûy qua phán têch caïc âiãöu hoìa tháúy nãúu biãn âäü cuía âiãöu hoìa cå baín cuía aïp laì 100% thç biãn âäü cuía âiãöu hoìa báûc 3chè coï 15%, coìn biãn âäü cuía âiãöu hoìa báûc 5 chè coìn coï 10%. Coìn caïc âiãöu hoìa khaïc vç biãn âäü quaï nhoí nãn khäng chuï yï âãún. Thäng thæåìng caïc chuäùi cuía nhæîng haìm chu kyì âæåüc cho åí caïc cáøm nang toaïn hoüc. Cuîng coï thãø phán têch tæì (5-3), (5-4) , (5-5). Trë hiãûu duûng vaì cäng suáút doìng chu ky ì Trë hiãûu duûng : Ta âaî biãút âãø âo khaí nàng sinh cäng cuía doìng chu kyì ta duìng trë 1T 2 T∫ hiãûu duûng I laì giaï trë trung bçnh bçnh phæång cuía haìm chu kyì : I = i dt (5-7). 0 Giaí sæí læåüng chu kyì khäng âiãöu hoìa i âæåüc phán tich thaình täøng caïc âiãöu hoìa coï ∞ 1T ∞ táön säú khaïc nhau i0, i1, i2, ik : i = ∑ ik(5-8) ta âæåüc I = ∫ (∑ i k ) 2 dt (5-9) 2 0 T0 0 Taïch bçnh phæång cuía täøng caïc säú haûng ik thaình 2 täøng, täøng thæï nháút gäöm nhæîng säú haûn ik2 vaì täøng thæï hai gäöm nhæîng säú haûng daûng ik il våïi ik ≠ il. Ta âæa têch phán vãö daûng : ∞ ∞ 1T 2T I2 = ∑ ∫ i 2 dt + ∑ k ∫ i k i l dt , säú haûng thæï hai bàòng 0, coìn säú haûng thæï nháút : 0 T0 k ,l =0 , k ≠ l T 0 ∞ 1T I2 = ∑ ∫ i 2 dt . k 0 T0 ∞ Trong âoï ik laì nhæîng haìm âiãöu hoìa æïng våïi táön säú khaïc nhau, nãn : I 2 = ∑ I 2 k 0 I = I + I + I + ... + I 2 0 2 1 2 2 2 k (5-10) U = U 0 + U 1 + U 2 + ... + U 2 2 2 2 k (5-11) Tæång tæû coï : E = E 0 + E 1 + E 2 + ... + E 2 2 2 2 k (5-12) Cäng suáút doìng chu kyì : Cäng suáút taïc duûng : P = I2 R thay I2 = ΣIk2 ta coï : Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 68 ∞ P = (I20+ I21+I22+...+ I2k) R = P0 + P1 + P2 + ...+ PK = ∑P 0 K (5-13) ∞ Vaì vç : Pk = Uk.Ikcosϕk nãn P= ∑U 0 I cosΨk K k (5-14) Tênh læûa choün âäúi våïi táön säú cuía caïc thäng säú täøng tråí, täøng dáùn : Ta biãút XL = ωL, Xc= 1/ω.C, XL1= ωL thç XLk = kωL = kXL1 (5-15) Xc1 = 1/ωC thç XCk = 1/kω C = XC1/ k (5-16) ⎫ Z K = R + j( kx L 1 − x C 1 / k ) = z k < ϕ k ⎪ ⎪ Nãn täøng tråí våïi soïng báûc k : z k = R 2 + ( k ω L − 1 2 ⎪ ) ⎬ (5-17) kω C ⎪ kω L − 1 / kω C ⎪ ϕ k = arctg ⎪ R ⎭ Phæång phaïp xeït maûch tuyãún tênh coï nguäön chu kyì khäng âiãöu hoìa Vç kêch thêch chu kyì khäng âiãöu hoìa theo Fourier âæåüc phán têch thaình täøng caïc kêch thêch thaình pháön chu kyì âiãöu hoìa khaïc nhau, nãn coï thãø coi kêch thêch taïc âäüng vaìo maûch gäöm caïc kêch thêch thaình pháön coï táön säú khaïc nhau. Theo nguyãn tàõc xãúp chäöng ta coï thãø tênh âaïp æïng æïng våïi tæìng kêch thêch thaình pháön, xong xãúp chäöng caïc âaïp æïng thaình pháön ta seî âæåüc âaïp æïng chung, æïng våïi kêch thêch chu kyì khäng âiãöu hoìa. Viãûc tênh âaïp æïng thaình pháön æïng våïi khêch thêch thaình pháön (kêch thêch æïng våïi mäüt táön säú xaïc âënh ) laì chu kyì âiãöu hoìa nãn duìng phæång phaïp phæïc tênh ráút thuáûn låüi, chè cáön læu yï luïc tênh våïi kêch thêch åí táön säú naìo thç täøng tråí phaíi âæåüc tênh theo táön säú âoï. Sau khi tênh âæåüc caïc âaïp æïng thaình pháön dæåïi daûng phæïc ta chuyãøn sang daûng tæïc thåìi âãø xãúp chäöng âæåüc caïc âaïp æïng chung (læu yï khäng xãúp chäöng nhæîng aính phæïc cuía nhæîng âiãöu hoìa táön säú khaïc nhau). .i (t) = Σik(t), u(t) = Σuk(t), e(t) = Σek(t) (5-18) Coìn giaï trë hiãûu duûng thç ta coï theo (5-10), (5-14). I = ΣI k , U = ΣU 2 , P = ΣPk 2 k Tæì phán têch trãn ruït ra caïc bæåïc giaíi maûch chu kyì khäng âiãöu hoìa: Phán têch kêch thêch chu kyì khäng âiãöu hoìa thaình täøng nhæîng kêch thêch chu kyì âiãöu hoìa coï táön säú khaïc nhau (thäng thæåìng bæåïc naìy khäng phaíi laìm maì âæåüc cho træåïc) Tênh täøng tråí phæïc caïc nhaïnh theo caïc táön säú. Duìng phæång phaïp phæïc tênh caïc âaïp æïng thaình pháön æïng våïi tæìng táön säú. Xãúp chäöng caïc âaïp æïng thaình pháön âãí âæåüc caïc âaïp i(t) æïng chung. 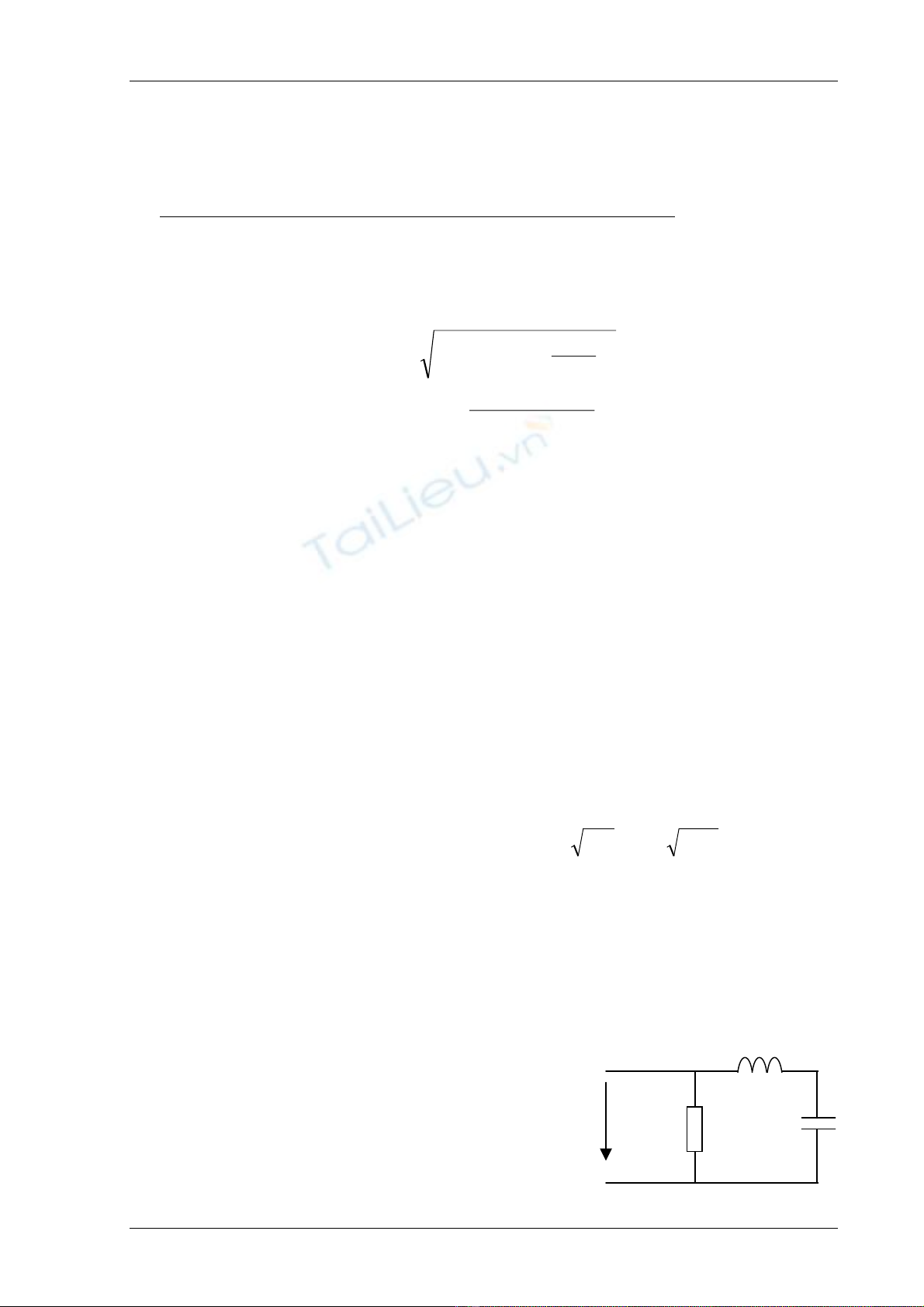L Vê duû : Giaíi maûch âiãûn nhæ hçnh (h.5-2). Biãút u(t) =100+141sin 100t, R=10Ω, XL1= 20Ω, XC1= 1/ωC= u(t) R C 10Ω. Xaïc âënh i, I , P trong maûch ? Giaíi: Âáy laì baìi toaïn maûch chu kyì khäng âiãöu hoìa. Kêch h.5-2 Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 69 thêch gäöm thaình pháön 1 chiãöu U0=100V thaình pháön âiãöu hoìa táön säú ω laì u1(t) = 141sin100t (âaî âæûåc phán têch Fourier). Ta tênh våïi tæìng kêch thêch thaình pháön . Khi chè coï U0=100V taïc duûng : I0=U0/R =100/10 =10 A cäng suáút tiãu thuû : P0 = I20 R =102.10 =1000 W. . Khi chè coï U 1 = 141 < 00 taïc duûng : Täøng tråí nhaïnh L- C laì : Z1LC= j (ωL- 1/ω C) = j(20 - 10) = j10Ω. . U. Doìng qua nhaïnh L - C laì : I 1LC = 1 = 141/j10 = 14,1 < - π/2. Z 1LC . . U Doìng qua tråí R laì : I 1R = 1 = 141/10 = 14,1 < 0. R . . . Doìng trong nhaïnh chung : I1 = I1LC + I1R = - j14,1 + 14,1 = 2 .14,1〈−450 ↔ i1(t) = 2 .14,1 sin (100t - 450) P1 = I21RR = (14,1/ 2 )2.R= 14,12.10/2 = 980 W 141 P1 = U1.I1. cosϕ =( ). 14,1. cos450 = 980 W 2 Täøng håüp kãút quaí : Giaï trë tæïc thåìi cuía doìng âiãûn trong maûch : i(t) = io + i1(t) = 10 + 2 .14,1 sin (100t - 450) Giaï trë hiãûu duûng doìng âiãûn trong maûch : I = I 0 + I1 = 10 2 + 14,12 ≈ 17 A 2 2 Cäng suáút taïc duûng trong maûch : P = P0 + P1 = 1000 + 980 =1980 W . Phäø táön cuía haìm chu kyì khäng âiãöu hoìa Phäø biãn âäü vaì phäø pha : Ta biãút coï thãø khai triãøn mäüt haìm thåìi gian chu kyì khäng âiãöu hoìa thaình chuäùi Fourier ∞ daûng : ƒ(ωt) = ∑F 0 km cos (kωt + Ψk). trong âoï biãn âäü vaì goïc pha cuía caïc thaình pháön âiãöu hoìa phuû thuäüc táön säú theo nhæîng qui luáût hoaìn toaìn tuìy thuäüc riãng daûng ƒ(ωt) : Fkm = Fkm(ω) , Ψk = Ψkm(ω) (5-19) goüi Fkm(ω) : phäø biãn âäü Ψkm(ω) : phäø pha cuía haìm chu kyì - goüi chung laì phäø táön säú. Våïi càûp phäø táön biãn, pha xaïc âënh tæång æïng coï haìm thåìi gian xaïc âënh . Vç váûy ta coï quan hãû doïng âäi giæîa mäüt càûp phäø táön våïi mäüt haìm thåìi gian . ƒ(ωt) ↔[ Fkm(ω),Ψkm(ω) ] (5-20) Âäúi våïi caïc haìm chu kyì ƒ(ωt) thç Fkm(ω) vaì Ψkm(ω) khäng triãût tiãu åí caïc âiãøm råìi raûc kω (k nguyãn dæång 0,1, 2, 3...) trãn truûc táön säú . 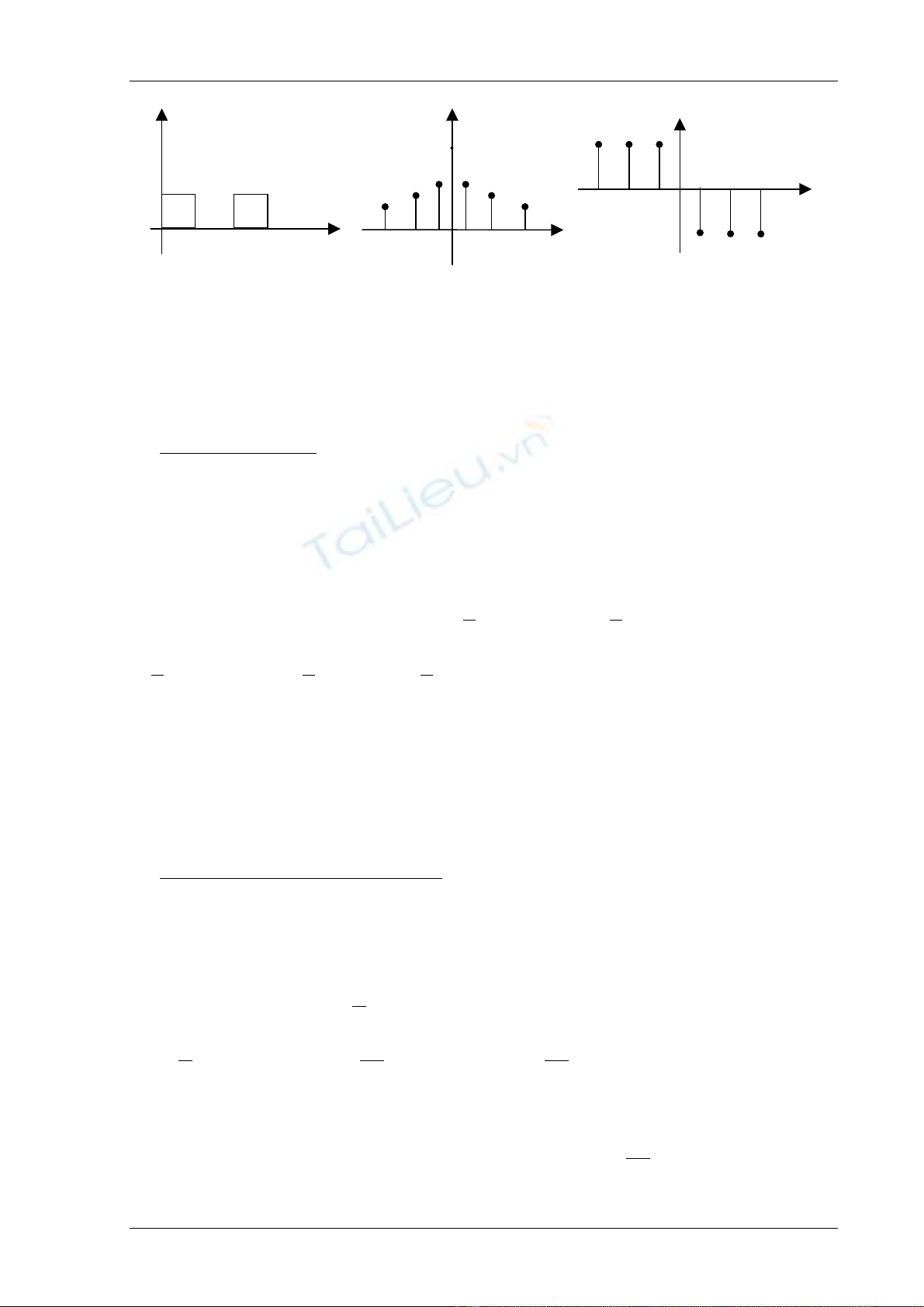⎧1 → 0 < ωt < π Vê duû : Tçm phäø táön cuía haìm thåìi gian hçnh (h.5-3) : e(ωt) = ⎨ ⎩0 → π < ωt < 2π Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 70 ψk e Ekm 1 900 ω 3ω 5ω ω -5ω -3ω -ω ωt 0 0 π 2π 3π -5ω -3ω -ω ω 3ω 5ω -900 h.5-3 h.5-4 h.5-5 Váûy phäø cuía haìm chu kyì laì nhæîng haìm råìi raûc vaì giaïn âoaûn cuía táön säú nãn goüi laì phäø giaïn âoaûn hay phäø vaûch. Tæì âoï cuîng tháúy khi haìm khäng chu kyì, tæïc laì haìm coï T = ∞ thç luïc âoï caïc vaûch phäø seî xêt laûi nhau, phäø seî liãn tuûc theo táön säú. Váûy mäüt haìm khäng chu kyì seî coï caïc phäø táön liãn tuûc, coìn goüi laì phäø âàûc. Daûng phæïc cuía phäø : ÅÍ mäùi táön säú kω phäø táön xaïc âënh mäüt càûp säú mäâun - argumen (Fkm, ψkm) vç váûy . . coï thãø biãøu diãùn bàòng säú phæïc F km = Fkm e jψ km . Caïc säú phæïc F km (ω) phán bäú råìi raûc theo táön säú laìm thaình mäüt phäø táön phæïc. Cáön xaïc âënh quan hãû giæîa haìm thåìi gian f(ωt) . vaì phäø táön F km (ω) . Tæì : ∞ 1∞ 1 ∞ f (ωt ) = f 0 + ∑ Fkm cos(kωt + ψ k ) = f 0 + ∑ Fkm e jψ e jkωt + ∑ Fkm e − jψ e − jkωt k k 1 2 1 2 1 ∞ 1 1 ∞ . 1 . . = ∑ 2 −∞ Fkm e jψ e jkωt = ∑ F km e jkωt , F 0 m e jψ = f 0 → F 0 m = 2f 0 , ψ 0 = 0 k 2 −∞ 2 0 (5-21) . F km (ω) = Fkm (ω)e jψ k (ω) Váûy daûng phæïc cuía phäø hay phäø phæïc laì mäüt haìm coï giaï trë phæïc råìi raûc cuía táön säú ω. Trë tuyãût âäúi cuía haìm âoï laì phäø biãn âäü coìn argumen laì phäø pha. Phäø phæïc laì mäüt caïch biãøu diãùn ráút goün tên hiãûu thåìi gian bàòng mäüt haìm giaï trë phæïc cuía táön säú ráút tiãûn duûng trong tênh toaïn phán têch quaï trçnh. Tênh phäø phæïc theo tên hiãûu âaî cho : Tæì cäng thæïc (5-21) ta tçm âæåüc haìm thåìi gian theo phäø phæïc âaî cho. Ngæåüc laûi ta tçm âæåüc phäø phæïc theo haìm thåìi gian âaî cho. . . Âãø tçm phäø phæïc F km (ω) cáön tçm säú phæïc F km æïng våïi caïc táön säú kω. Muäún váûy 1 nhán hai vãú cuía (5-21) våïi e-jkωt vaì láúy têch phán theo ωt trong mäüt chu kyì ta âæåüc : π 2π 1 1 2π • ∞ 1 2π • ∫ f (ωt )e − jkωt d (ωt ) = ∫ F km d (ωt ) + ∑ ∫ F lm e j ( l − k ) ωt d ( ωt ) π0 2π 0 l = −∞ , k ≠ l 2 π 0 . Theo Euler caïc säú haûng daûng F lm e j( l − k ) ωt våïi l≠k laì täøng cuía hai haìm âiãöu hoìa nãn 1 2π . . 2π ∫ têch phán cuía chuïng trong mäüt chu kyì bàòng 0 vaì têch phán F km .d (ωt ) = F km nãn 0 ta âæåüc cäng thæïc : Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 71 . 1 2π F km = ∫ f (ωt ).e d (ωt ) − jkωt (5-22) π0 . Nãúu k laì mäüt säú âaî cho thç cäng thæïc (5-22) cho F km laì mäüt säú phæïc æïng våïi táön säú kω. Nãúu coi k laì thäng säú chaûy thç (5-22) cho mäüt haìm säú phæïc cuía kω hay cuía ω vaì âoï chênh laì phäø phæïc cáön tçm cuía haìm thåìi gian f(ωt). Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2431 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.