Tổ Tin Học
Trang 9 Chủ biên Võ Thanh Ân
CHƯƠNG 2: HÀM LOGIC
9 HÀM LOGIC CƠ BẢN
9 CÁC DẠNG CHUẨN CỦA HÀM LOGIC
• Dạng tổng chuẩn
• Dạng tích chuẩn
• Dạng số
• Biến đổi qua lại giữa các dạng chuẩn
9 RÚT GỌN HÀM LOGIC
• Phương pháp đại số
• Phương pháp dùng bảng Karnaugh
• Phương pháp Quine Mc. Cluskey
I. HÀM LOGIC CƠ BẢN
1. Một số định nghĩa
- Trạng thái logic được biểu diễn bằng số 0 hoặc 1.
- Biến logic là đại lượng biễu diễn bởi một ký hiệu (chữ hay dấu) chỉ gồm các
giá trị 0 hay 1 tuỳ theo điều kiện nào đó.
- Hàm logic diễn tả một nhóm biến logic liên hệ với nhau bởi các phép toán
logic. Cũng như biến logic, hàm logic chỉ nhận 1 giá trị 0 hoặc 1.
2. Biểu diễn biến và hàm logic
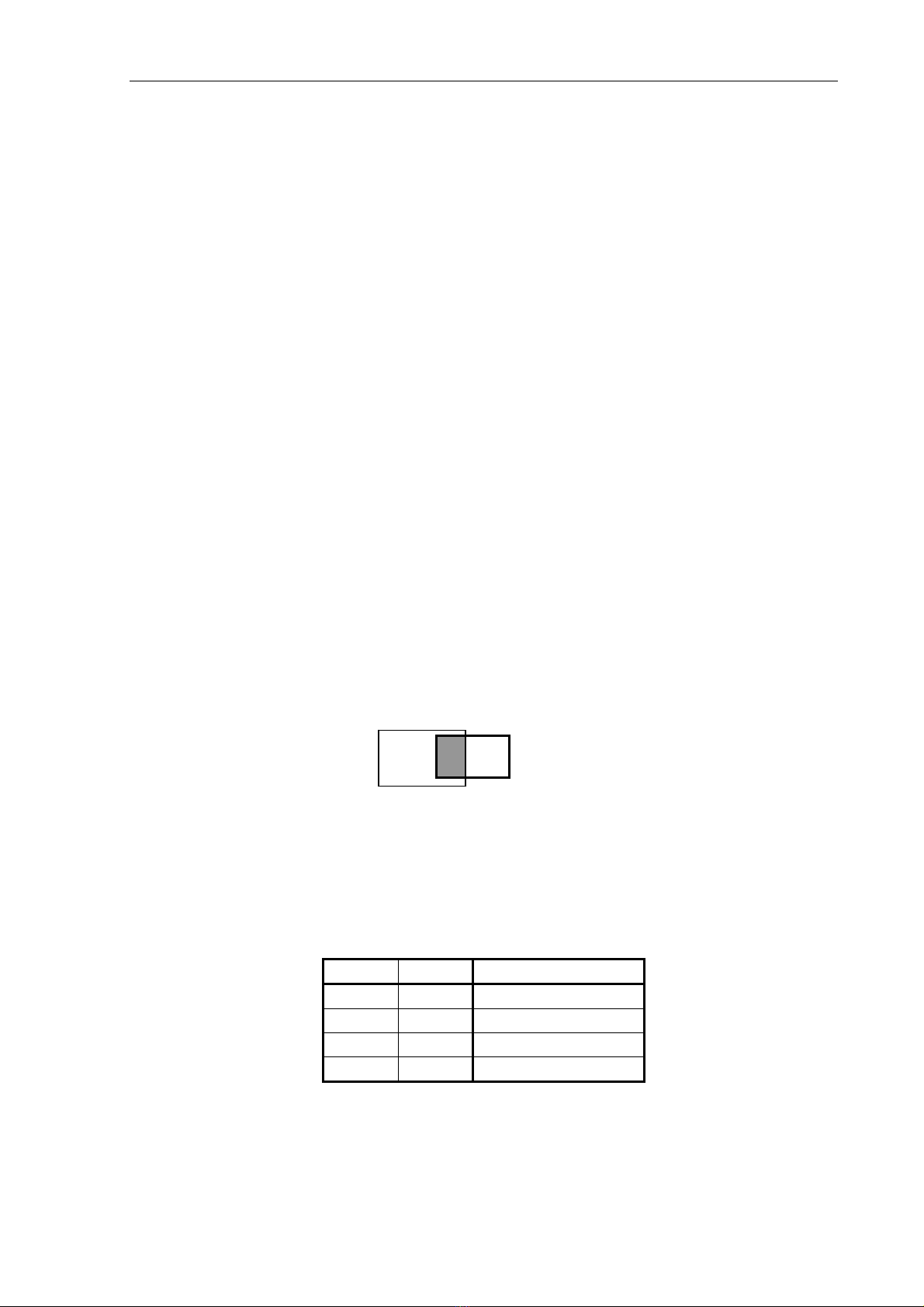
a. Giản đồ Venn
Còn gọi là giản đồ Euler, đặc biệt dùng trong lĩnh vực tập hợp. Mỗi biến logic
chia không gian ra 2 vùng không gian con, 1 vùng trong đó giá trị biến là đúng hay 1,
vùng còn lại là vùng phụ trong đó giá trị biến là sai hay 0.
Ví dụ: Phần giao nhau của 2 tập hợp A và B (màu xám) biểu diễn tập hợp trong
đó A và B đúng (A and B = 1).
b. Bảng sự thật
Nếu hàm có n biến, bảng sự thật có n + 1 cột và 2n + 1 hàng. Hàng đầu tiên chỉ
tên biến và hàm, các hàng còn lại trình bày những tổ hợp của n biến, có cả thảy 2n tổ
hợp có thể có. Các cột ghi tên biến, cột cuối cùng ghi tên hàm và giá trị của hàm tương
ứng với các tổ hợp biến trên cùng hàng.
Ví dụ: Hàm F(A,B) = A OR B có bảng sự thật như sau:
A B F(A,B) = A OR B
0 0 0
0 1 1
1 0 1
1 1 1
A B
Giáo trình Kỹ Thuật Số
Chủ biên Võ Thanh Ân Trang 10
c. Bảng Karnaugh
Đây là cách biểu diễn khác của bảng sự thật trong đó mỗi hàng của bảng sự thật
được thay thế bởi 1 ô mà tọa độ hàng và cột có giá trị xác định bởi tổ hợp đã cho của
biến.
Bảng Karnaugh của hàm có n biến gồm 2n ô. Bảng Karnaugh rất thuận tiện để
đơn giản hàm logic bằng cách nhóm các ô lại với nhau.
Ví dụ: Hàm F(A,B) = A OR B có bảng Karnaugh như sau:
B
A 0 1
0 0 1
1 1 1
d. Giản đồ thời gian
Dùng để diễn tả quan hệ giữa hàm và biến theo thời gian.
Ví dụ: Hàm F(A,B) = A OR B có bảng giản đồ thời gian như sau:
A
T
B
T
F(A,B)
T
3. Qui ước
Khi nghiên cứu một hệ thống logic, cần xác định qui ước logic. Qui ước này
không được thay đổi trong suốt quá trình nghiên cứu.
Ví dụ: Trong một hệ thống số có 2 giá trị điện áp 0V (thấp) và 5V (cao), ta có thể
chọn một trong hai qui ước sau:
Điện áp Logic dương Logic âm
0V
5V
1
0
0
1
4. Các hàm logic cơ bản
a. Hàm NOT (đảo, bù)
Phép toán (gạch trên):⎯
Bảng sự thật dưới đây:
A
Y
=
A A
Y
=
0 1
1 0
Tổ Tin Học
Trang 11 Chủ biên Võ Thanh Ân
b. Hàm OR (hoặc)
Phép toán: + (cộng).
Bảng sự thật dưới đây.
A B F(A,B) = A + B
0 0 0
0 1 1
1 0 1
1 1 1
c. Hàm AND (và)
Phép toán: • (nhân – dấu chấm).
Bảng sự thật dưới đây.
A B F(A,B) = A.B
0 0 0
0 1 0
1 0 0
1 1 1
d. Hàm EX–OR (OR loại trừ)
Phép toán: ⊕ (exor).
Bảng sự thật dưới đây.
A B
F(A,B) = A
⊕
B
0 0 0
0 1 1
1 0 1
1 1 0
5. Tính chất của các hàm logic cơ bản
a. Tính chất cơ bản
- Có một phần tử trung tính duy nhất cho mỗi toán tử + (cộng) và . (nhân).
A + 0 = A ;0 là phần tử trung tính của hàm OR.
A .1 = A ;1 là phần tử trung tính của hàm AND.
- Tính chất giao hoán.
A + B = B + A
A . B = B . A
- Tính phối hợp.
(A + B) + C = A + (B + C) = A + B + C
(A . B) . C = A . (B . C) = A . B . C
- Tính phân bố.
Phép nhân: A . (B + C) = A . B + A . C
Phép cộng: A + (B . C) = (A + B) . (A + C)
- Không có phép tính lũy thừa và thừa số.
Giáo trình Kỹ Thuật Số
Chủ biên Võ Thanh Ân Trang 12
A + A + … + A = A
A . A . … . A = A
- Tính bù.
0.
1AA
=
=+
=
AA
AA
b. Tính song đối (duality)
Tất cả các biểu thức logic vẫn đúng khi ta thay phép toán + (cộng) bởi phép toán
• (nhân), 0 bởi 1 hay ngược lại.
Ta hãy xét các ví dụ sau:
A + B = B + A Ù A . B = B . A
BABAA +=+ Ù BABAA .)(. =+
A + 1 = 1 Ù A . 0 = 0
c. Định lý De Morgan
Định lý De Morgan được phát biểu bởi 2 biểu thức sau:
CBACBA
CBACBA
++=
=++
..
..
Định lý trên cho phép biến đổi qua lại giữa phép nhân và phép cộng nhờ vào
phép đảo.
d. Sự phụ thuộc lẫn nhau của các hàm logic cơ bản
Định lý De Morgan cho ta thấy các hàm logic không độc lập với nhau. Chúng có
thể biến đổi qua lại do đó chúng ta có thể dùng hàm [AND và NOT] hoặc [OR và
NOT] để biểu diễn tất cả các hàm.
Ví dụ: Chỉ dùng hàm AND và NOT biễu diễn hàm: CABCABY ++=
Chỉ việc đảo Y hai lần ta được kết quả: CABCABCABCABYY ..=++==
II. CÁC DẠNG CHUẨN CỦA HÀM LOGIC
1. Giới thiệu
Hàm logic được biễu diễn bởi tổ hợp của những tổng và tích logic.
Nếu là tổng của những tích ta có dạng: ZYXZXYZYXf ++=),,(
Nếu là tích của những tổng ta có dạng: ))()((),,( ZYZXYXZYXf +++=
Một hàm logic được gọi là hàm chuẩn nếu mỗi số hạng chứa đầy đủ các biến. Ta
hãy xem hàm sau: ZYXZYXXYZZYXf ++=),,( là một tổng chuẩn. Mỗi số hạng của
tổng chuẩn gọi là minterm.
Ta hãy xem hàm sau: ))()((),,( ZYXZYXZYXZYXf ++++++= là một tích
chuẩn. Mỗi số hạng của tích chuẩn gọi là maxterm.
Tổ Tin Học
Trang 13 Chủ biên Võ Thanh Ân
2. Dạng tổng chuẩn
Để có hàm logic dưới dạng chuẩn ta áp dụng định lý triển khai của Shanon. Dạng
tổng chuẩn có thể triển khai theo định lý Shanon thứ nhất.
Tất cả các hàm logic có thể triển khai theo một trong những biến dưới dạng tổng
của 2 tích như sau:
Z), B, (0,. Z), B, (1,A. Z), B, (A, …+…=… fAff
Ví dụ: Ta triển khai với hàm 2 biến f(A, B) như sau:
Khai triển theo biến A: ),0(.),1(.),( BfABfABAf +=
Mỗi hàm trong 2 hàm vừa tìm được, tiếp tục khai triển theo biến B:
)0,1(.)1,1(.),1( fBfBBf +=
)0,0(.)1,0(.),0( fBfBBf +=
Nhân vào ta được: )0,0(.)1,0(.)0,1(.)1,1(.),( fBAfBAfBAfABBAf +++=
Với mỗi cặp i, j ta có lượng giá trị f(i, j) biểu diễn một giá trị riêng của f(A, B)
trong bài toán phải giải.
Với hàm 3 biến, khai triển ta được:
)0,0,0(.)1,0,0(.)0,1,0(.)1,1,0(.
)0,0,1(.)1,0,1(.)0,1,1(.)1,1,1(.),,(
fCBAfCBAfCBAfBCA
fCBAfCBAfCABfABCCBAf
++++
++++=
Khai triển hàm n biến, ta được 2n số hạng.
Mỗi số hạng trong triển khai là tích của một tổ hợp biến và một trị riêng của hàm.
Có hai trường hợp có thể xảy ra:
- Giá trị riêng bằng 1, số hạng thu gọn chỉ còn biến.
CBAfCBA =)1,0,0(. nếu f(0,0,1) = 1.
- Giá trị riêng bằng 0, số hạng nhân hàm bằng 0. Số hạng này biến mất trong
biểu thức tổng (theo qui tắc X + 0 = X).
0)1,0,0(. =fCBA nếu f(0,0,1) = 0 (theo qui tắc X.0 = 0).
Ví dụ: Cho hàm 3 biến A, B, C xác định bởi bảng sự thật sau, viết dạng hàm tổng
chuẩn cho hàm:
Hàng A B C Z = f(A, B, C)
0 0 0 0 0
1 0 0 1 1 = f(0,0,1)
2 0 1 0 1 = f(0,1,0)
3 0 1 1 1 = f(0,1,1)
4 1 0 0 0
5 1 0 1 1 = f(1,0,1)
6 1 1 0 0
7 1 1 1 1 = f(1,1,1)
- Hàm Z có trị riêng f(0,0,1) = 1 tương ứng với giá trị của tổ hợp biến ở
“Hàng 1” là A = 0, B = 0, C = 1. Tổ hợp này là CBACBAfCBA == 1.)1,0,0(.
là một số hạng trong tổng chuẩn
- Tương tự các tổ hợp (2), (3), (5), (7) cũng là các số hạng của tổng chuẩn.
- Cuối cùng ta có: ABCCBABCACBACBAZ ++++=