Chöông 1: Toång quan veà maïng Neural
- 1 -
Chöông I
TOÅNG QUAN VEÀ MAÏNG NEURAL
I. LÒCH SÖÛ PHAÙT TRIEÅN CUÛA MAÏNG NEURAL
Naêm 1936, Alan Turing laø ngöôøi ñaàu tieân xem boä naõo nhö moät moâ hình xöû lyù
thoâng tin. Naêm 1943, Warren McCulloch vaø Walter Pitts ñaõ ñeà xuaát caùch hoaït ñoäng
cuûa caùc Neural, hoï ñaõ taïo ra moät maïng Neural ñôn giaûn baèng caùc maïch ñieän. Töø ñoù
caùc nhaø khoa hoïc lao vaøo nghieân cöùu caùc boä maùy thoâng minh.
Naêm 1949, Donall Hebb ñeà xuaát moät giaûi thuaät huaán luyeän maïng Neural raát noåi
tieáng, maø ngaøy nay noù vaãn coøn ñöôïc söû duïng .
Thaäp nieân 50 laø thôøi kyø maø maïng Neural phaùt trieån caû phaàn cöùng laãn phaàn
meàm. Nathaniel Rochester vaø moät soá ngöôøi khaùc töø caùc phoøng thí nghieäm cuûa IBM
ñaõ xaây döïng phaàn meàm moâ phoûng maïng Neural döïa treân giaûi thuaät cuûa Hebb.
Naêm 1957, Frank Roseblantt baét ñaàu nghieân cöùu veà maïng Perceptron vaø ñaõ
thaønh coâng trong vieäc thieát keá Mack I Perceptron nuerocomputer, ñoù laø maïng
Neural coå ñieån nhaát vaãn coøn söû duïng ñeán ngaøy nay .
Naêm 1959, Bernard Widrow vaø Marcian Hoff ñaõ xaây döïng maïng Adaline, noù laø
aùp duïng ñaàu tieân cuûa maïng Neural vaøo thöïc teá ñeå daäp tieáng voïng treân ñöôøng daây
ñieän thoaïi.
Naêm 1967, Avanlanche aùp duïng caùc maïng Neural vaøo vieäc nhaän daïng gioïng
noùi, ñieàu khieån motor vaø moät soá öùng duïng khaùc.
Töø naêm 1969 ñeán naêm 1981 maïng Neural rôi vaøo traïng thaùi im laëng caû veà
nghieân cöùu vaø öùng duïng. Tuy nhieân, coù theå keå ñeán baøi baùo caùo cuûa Marvin Minsky
vaø Seymour Papert bình luaän veà maïng perceptron, caùc nghieân cöùu veà quaù trình hoïc
cuûa maïng nhieàu lôùp, maïng töï toå chöùc ( Self Organization ) cuûa Teuvo Kohonen,
maïng kieåu boä nhôù keát hôïp ( BAM – Bidirectional Associative Memory ) cuûa
Anderson vaø maïng ART ( Adaptive Resonance Theory Neural Networks ) cuûa
Capenter.
Naêm 1982, John Hopfield coâng boá moät coâng trình veà maïng Neural moät lôùp treân
National Academy of Sciences, noù ñöôïc coi laø moät ñoäng löïc loâi keùo caùc nhaø khoa
hoïc quay trôû laïi nghieân cöùu veà maïng Neural. Ñaây laø thôøi kyø phuïc höng cuûa caùc
nghieân cöùu vaø öùng duïng maïnh meõ cuûa maïng Neural vôùi caùc nghieân cöùu veà giaûi
thuaät lan truyeàn ngöôïc sai soá ( Backpropagation of error ), maïng Boltzmann, maïng
Neocognitron cuûa Fukushima.
Töø cuoái thaäp nieân 80, ñaàu thaäp nieân 90 ñeán nay, maïng Neural ñaõ khaúng ñònh
ñöôïc vò trí cuûa mình trong nhieàu öùng duïng khaùc nhau .
Chöông 1: Toång quan veà maïng Neural
- 2 -
II. MAÏNG NEURAL VAØ CAÙC KHAÙI NIEÄM CÔ BAÛN
II.1. Giôùi thieäu veà maïng Neural
Maïng Neural laø maïng maø ñöôïc xaây döïng baèng caùch sao cheùp laïi caùc nguyeân lyù
toå chöùc cuûa heä Neural con ngöôøi. Boä oùc con ngöôøi laø moät heä Neural goàm coù 1010
ñeán 1012 Neural ñöôïc toå chöùc coù caáu truùc vaøo khoaûng 200 moâ hình khaùc nhau döôùi
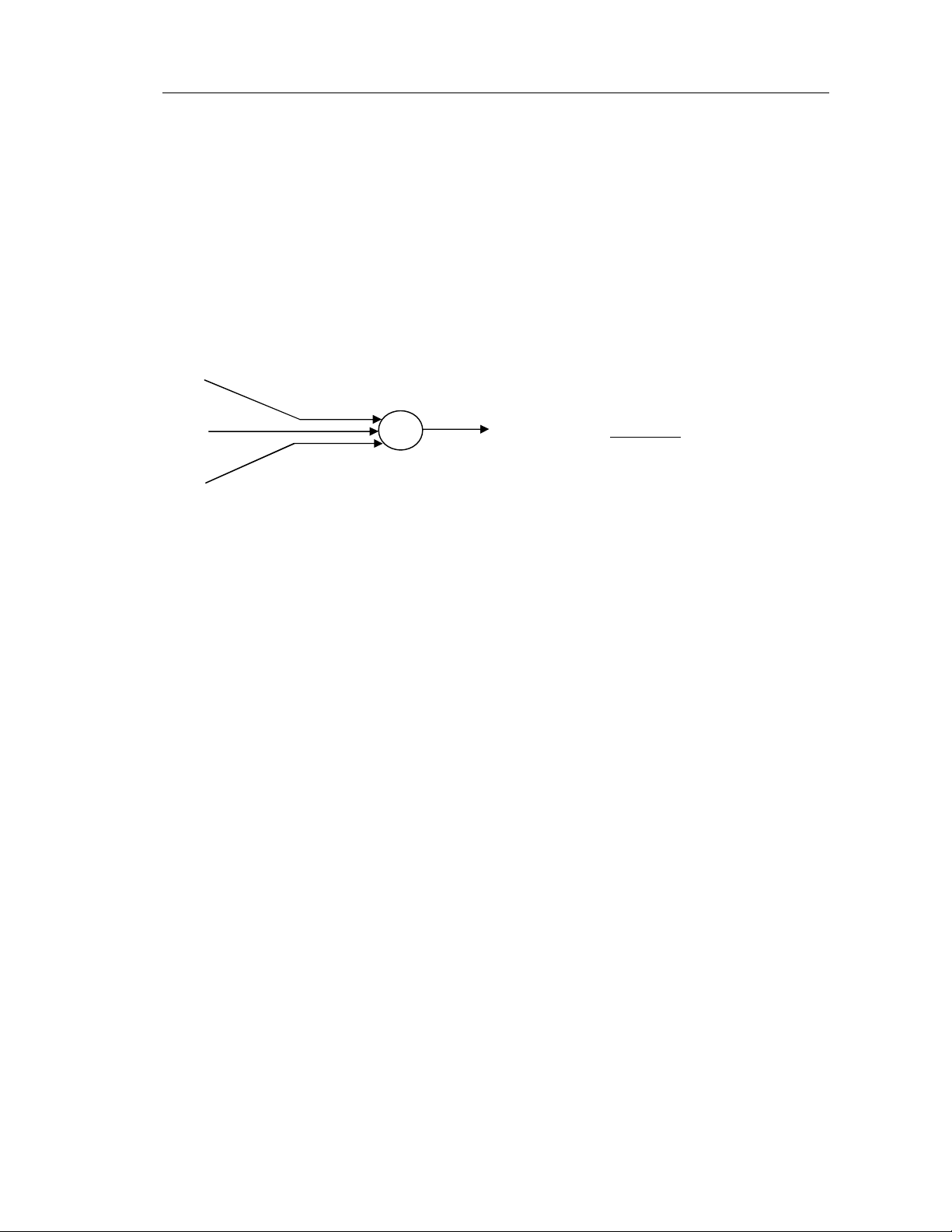
daïng nhieàu lôùp. Caáu truùc cô baûn cuûa moät Neural trong heä Neural con ngöôøi goàm coù
ñoù laø caùc ñaàu vaøo (input) thaân Neural vaø ñaàu ra (output). Thaân Neural laø phaàn töû xöû
lyù coù chöùc naêng thu thaäp taát caû caùc thoâng tin töø caùc ñaàu vaøo tính toaùn vaø ñöa ra caùc
quyeát ñònh ôû ngoõ ra ñeå göûi tín hieäu ñeán caùc Neural khaùc nhö moâ taû ôû hình 1.1.
Input Thaân Neural
Output
Moãi Neural coù nhieàu input nhöng chæ coù moät output, töø output naøy môùi reõ nhaùnh
ñöa thoâng tin ñeán caùc Neural khaùc. Trong maïng Neural nhaân taïo, tín hieäu truyeàn töø
Neural naøy ñeán Neural khaùc laø tín hieäu ñieän aùp. Coù hai loaïi tín hieäu ñieän aùp ñoù laø
ñieän aùp döông vaø ñieän aùp aâm. Ñieän aùp döông ñöôïc xem nhö laø tín hieäu kích ñoäng
(excitory) ñeå kích ñoäng Neural göûi tín hieäu ñeán caùc Neural khaùc vaø ñieän aùp aâm
ñöôïc xem nhö laø tín hieäu öùc cheá (inhibitory) ñeå öùc cheá Neural göûi tín hieäu ñeán caùc
Neural khaùc. Khi ñieän aùp laø zero thì khoâng coù söï lieân laïc giöõa hai Neural.
Cuõng gioáng nhö heä Neural con ngöôøi, maïng Neural nhaân taïo bao goàm lôùp ñaàu
vaøo, caùc lôùp aån vaø lôùp Neural ñaàu ra. Trong maïng, ñaàu ra cuûa Neural naøy keát noái
vôùi ñaàu vaøo cuûa nhieàu Neural khaùc hoaëc keát noái vôùi ñaàu vaøo cuûa Neural chính noù.
Cöôøng ñoä caùc keát noái xaùc ñònh löôïng tín hieäu truyeàn ñeán ñaàu vaøo. Giaù trò cuûa cöôøng
ñoä keát noái ñöôïc goïi laø troïng soá. Trong thôøi gian heä tieáp xuùc vôùi moät vaøi ñoái töôïng,
moät soá phaàn töû caûm bieán bò taùc ñoäng, cöôøng ñoä keát noái cuûa moät soá Neural thích hôïp
trong heä seõ ñöôïc gia taêng nhaèm cung caáp thoâng tin veà ñoái töôïng maø heä tieáp xuùc vaø
ñöa ra caùc quyeát ñònh ôû lôùp ñaàu ra. Quaù trình naøy ñöôïc goïi laø quaù trình hoïc, söï thay
ñoåi cuûa caùc troïng soá trong quaù trình naøy goïi laø luaät hoïc.
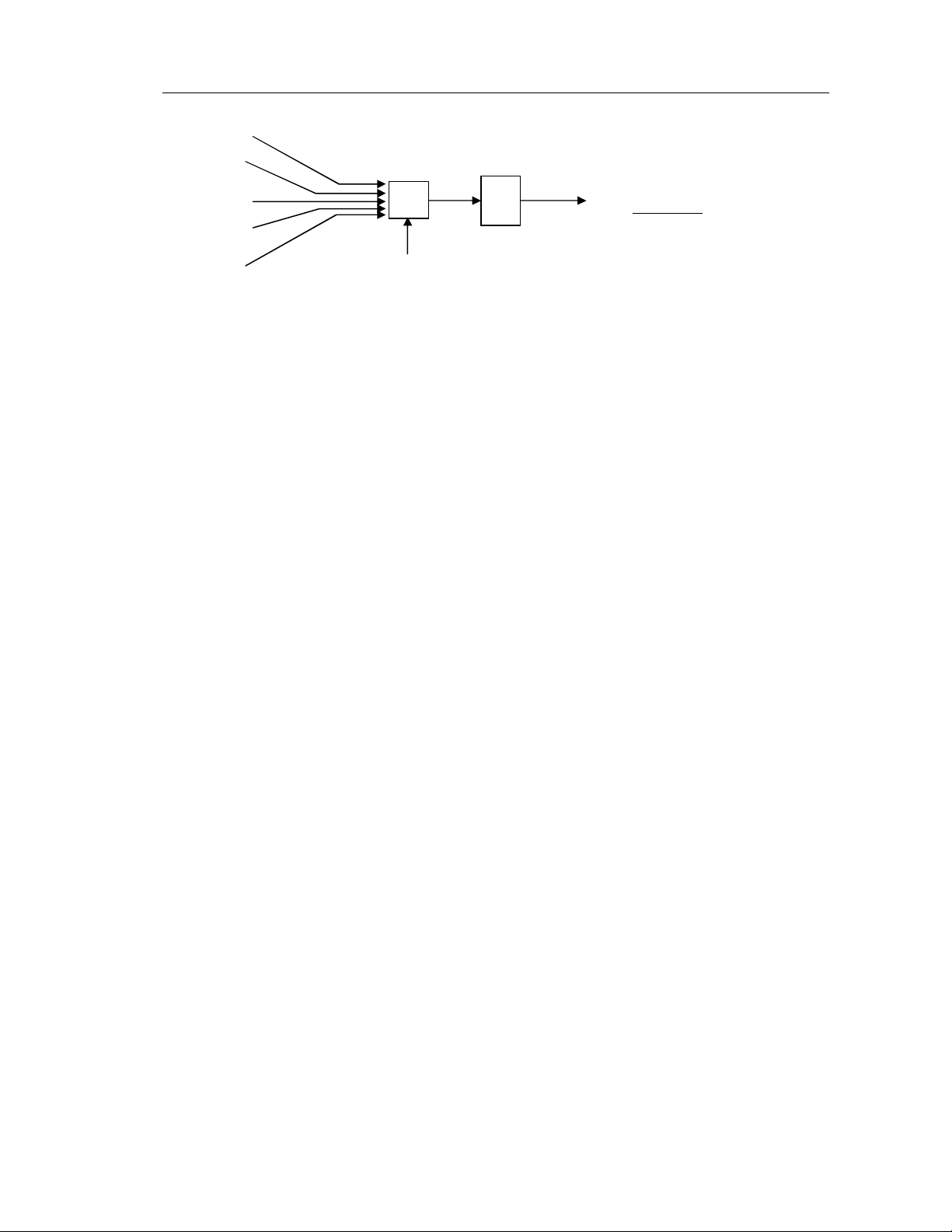
Ñeå xaây döïng moät maïng Neural gioáng nhö heä Neural con ngöôøi, yù töôûng ñaàu
tieân cuûa Mc.culloch vaø Pitts vaøo naêm 1943 ñeà ra caáu truùc cô baûn cuûa moät Neural thöù
i trong moâ hình cuûa maïng Neural nhaân taïo nhö hình 1.2.
Hình 1.1
Chöông 1: Toång quan veà maïng Neural
- 3 -
Trong ñoù:
- xj laø ñaàu ra cuûa Neural thöù j hoaëc ñaàu vaøo töù moâi tröôøng beân ngoaøi.
- wi,j laø troïng soá keát noái giöõa Neural thöù i vaø Neural thöù j.
- b laø moät haèng soá (Bias).
- ai laø ñaàu ra cuûa Neural thöù i.
- f laø haøm truyeàn.
- net laø ñoái soá cuûa haøm f.
net=wi,1.x1+wi,2.x2+…+wi,r.xr+b (1.1)
ai=f(n) (1.2)
Caùc thoâng soá:
+Ñaàu vaøo (input): Thoâng soá hay döõ lieäu ñaàu vaøo
+Ñaàu ra (output) : Thoâng soá hay döõ lieäu ñaàu ra
+ Troïng soá(Weight) : Keát noái giöõa hai Neural trong maïng Neural goïi laø troïng
soá, chuùng coù theå ñieàu chænh ñöôïc. Khi caùc tín hieäu ñöôïc ñöa vaøo Neural ñeå xöû lyù thì
noù ñöôïc nhaân vôùi heä soá aûnh höôûng cuûa maïng giöõa hai lôùp, goïi laø heä soá troïng soá w
vaø sau ñoù ñöôïc bieán ñoåi bôûi haøm phi tuyeán (haøm truyeàn).
+ Bias: Laø haèng soá ñöôïc ñöa tröïc tieáp vaøo maïng Neural thoâng qua boä toång,
cuõng coù theå ñöa vaøo maïng thoâng qua input vôùi troïng soá nhaân vôùi noù laø w=1. Bias
cho pheùp thay ñoåi ñöôøng phaân chia veà phía döôùi, hoaëc treân goác toaï ñoä.
+Toác ñoä daïy: Ñaây laø thoâng soá raát quan troïng, noù quyeát ñònh ñeán keát quaû cuûa
quaù trình huaán luyeän. Neáu n quaù lôùn thì quaù trình tính toaùn nhanh nhöng keát quaû
toaøn cuïc seõ khoâng tìm ñöôïc, ngöôïc laïi, neáu n quaù nhoû thì keát quaû toaøn cuïc tìm ñöôïc
nhöng soá böôùc tính toaùn laïi raát nhieàu. Ñeå quaù trình tính toaùn ñaït hieäu quaû ngöôøi ta
thöôøng choïn 0.1 < n < 1.
+ Haøm truyeàn (haøm kích hoaït, haøm hoaït ñoäng): Haøm truyeàn cuûa Neural ñöôïc
bieåu dieãn bôûi haøm f(x). Noù ñònh nghóa tín hieäu output cuûa Neural neáu tín hieäu input
ñaõ ñöôïc bieát tröôùc. Taùc duïng cuûa haøm truyeàn laø laøm cho caùc tín hieäu nhaäp gaàn vôùi
tính hieäu xuaát chuaån.
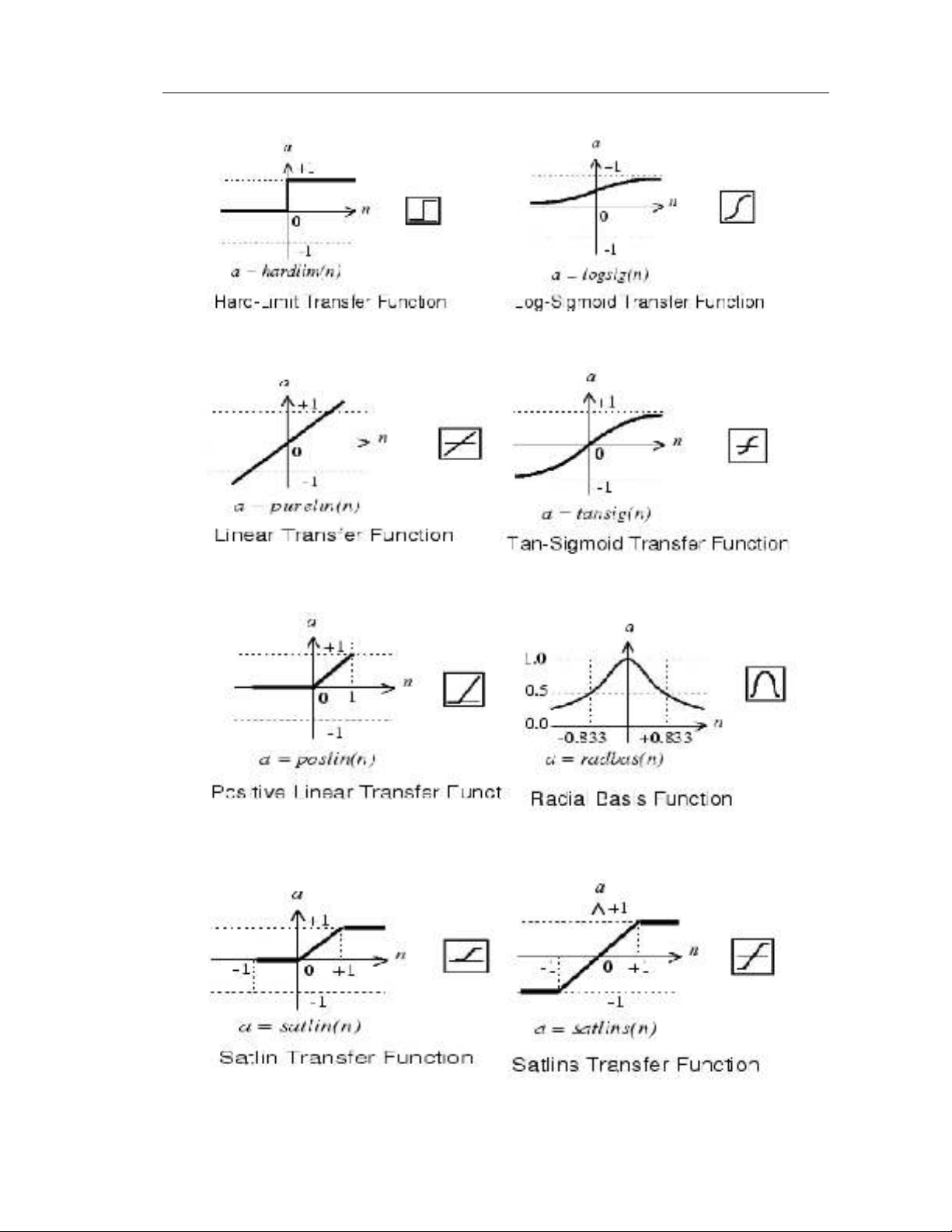
Coù caùc loaïi haøm hoaït ñoäng sau:
b
ai
Wi,1
Wi,2
Wi,r
Σ
f
x1
x2
x3
x4
xr
Hình 1.2
net
Chöông 1: Toång quan veà maïng Neural
- 4 -
Hình 1.3 Hình 1.4
Hình 1.5 Hình 1.6
Hình 1.7 Hình 1.8
Hình 1.9 Hình 1.10
Chöông 1: Toång quan veà maïng Neural
- 5 -
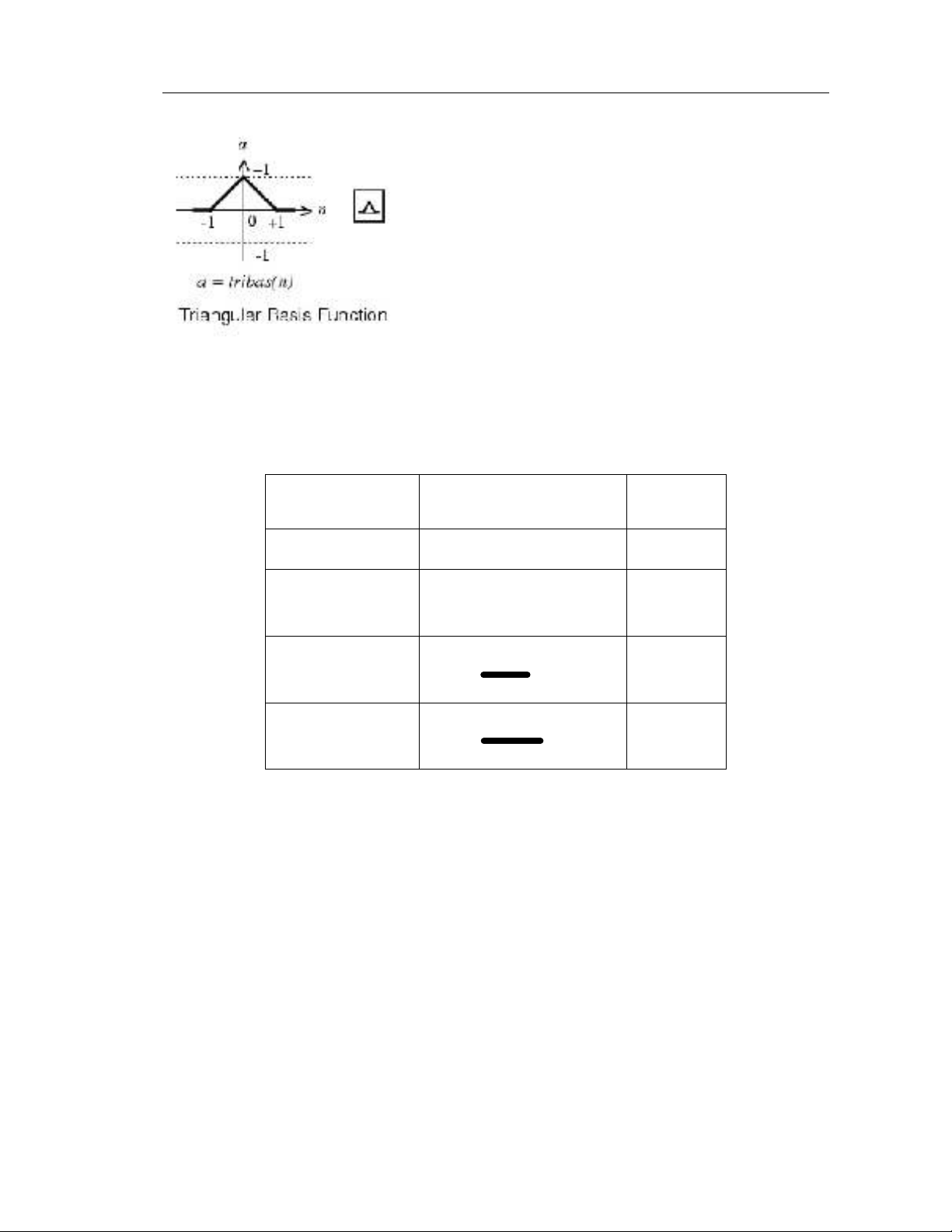
Hình 1.11
Trong noäi dung luaän vaên naøy chæ ñeà caäp ñeán 4 haøm thöôøng ñöôïc söû duïng sau:
Baûng 1.1
Loaïi haøm Phöông trình Hình veõ
Haøm tuyeán tính F(x)=x Hình 1.5
Haøm ngöôõng F(x)=
<
>
0x neáu 1-
0
x
neáu
1
Hình 1.3
Haøm Logsig x
e
)x(F
+
=
1
1 Hình 1.4
Haøm tansig 1
1
2−
+
=−ax
e
)x(F Hình 1.6
Vieäc löïa choïn haøm truyeàn aûnh höôûng ñeán thôøi gian daïy maïng vaø ñöôïc xaùc
ñònh bôûi:
- Ñaëc tính cuûa baøi toaùn (tuyeán tính, phi tuyeán, lieân tuïc, giaùn ñoaïn..)
- Thuaän lôïi cho vieäc öùng duïng maùy tính.
- Thuaät toaùn daïy maïng.
+ Lôùp (layer): Maïng Neural coù theå coù moät hay nhieàu lôùp. Lôùp ñaàu vaøo goïi laø
input layer, lôùp cuoái cuøng coù giaù trò ñaàu ra laø output thì goïi laø output layer (lôùp
output). Caùc lôùp coøn laïi goïi laø hidden layer (lôùp aån).
+Khaùi nieäm daïy maïng: laø quaù trình laøm thay ñoåi caùc thoâng soá trong maïng
(troïng soá, Bias) cho phuø hôïp vôùi kích thích beân ngoaøi, sau ñoù chuùng löu giöõ caùc giaù
trò naøy. Caùch daïy ñöôïc xaùc ñònh thoâng qua caùch thöùc thay ñoåi thoâng soá.