Giáo trình thủy lực - Trường Đại Học Kiến Trúc Tp.HCM - Chương 5

Chia sẻ: Mai Tron | Ngày: | Loại File: PDF | Số trang:9

Thêm vào BST

Báo xấu

160
lượt xem 19
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'giáo trình thủy lực - trường đại học kiến trúc tp.hcm - chương 5', kỹ thuật - công nghệ, kiến trúc - xây dựng phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giáo trình thủy lực - Trường Đại Học Kiến Trúc Tp.HCM - Chương 5

Chöông 5 DOØNG CHAÛY ÑEÀU TRONG OÁNG I. HAI TRAÏNG THAÙI CHAÛY Thí nghieäm Reynolds 1. Chaûy taàng : Khi vaän toác nhoû , Re = VD/ν < Regh Quaù ñoä: 2. Chaûy roái : Khi vaän toác lôùn , Re = VD/ν > Re gh Trong thí nghieäm nhaän thaáy: Regh(treân) Roái Taàng Taàng Roái Regh(döôùi) =2300 1 Löïc taùc duïng treân phöông L F1=p1dA doøng chaûy ( phöông s) : dA τ 2 ro r Gsinα α+ − − = F2=p2dA 1 − G α τ =0 γ + − −τ = z1 2 s τ z2 τ =τmax − + − − = γ γ γ Maët chuaån τ τ + − + − = + − + = γ γ γ γ γ γ PT N ng ⎛ ⎞ ⎛ ⎞ + + = + + + ⎜ ⎜ + ⎟−⎜ + ⎟= l ng (1-2) γ γ ⎝ γ ⎟ ⎜γ ⎠ ⎝ ⎟ ⎠ τL hd hd = τ = γR τ =γ Phöông trình cô baûn cuûa doøng ñeàu γR L 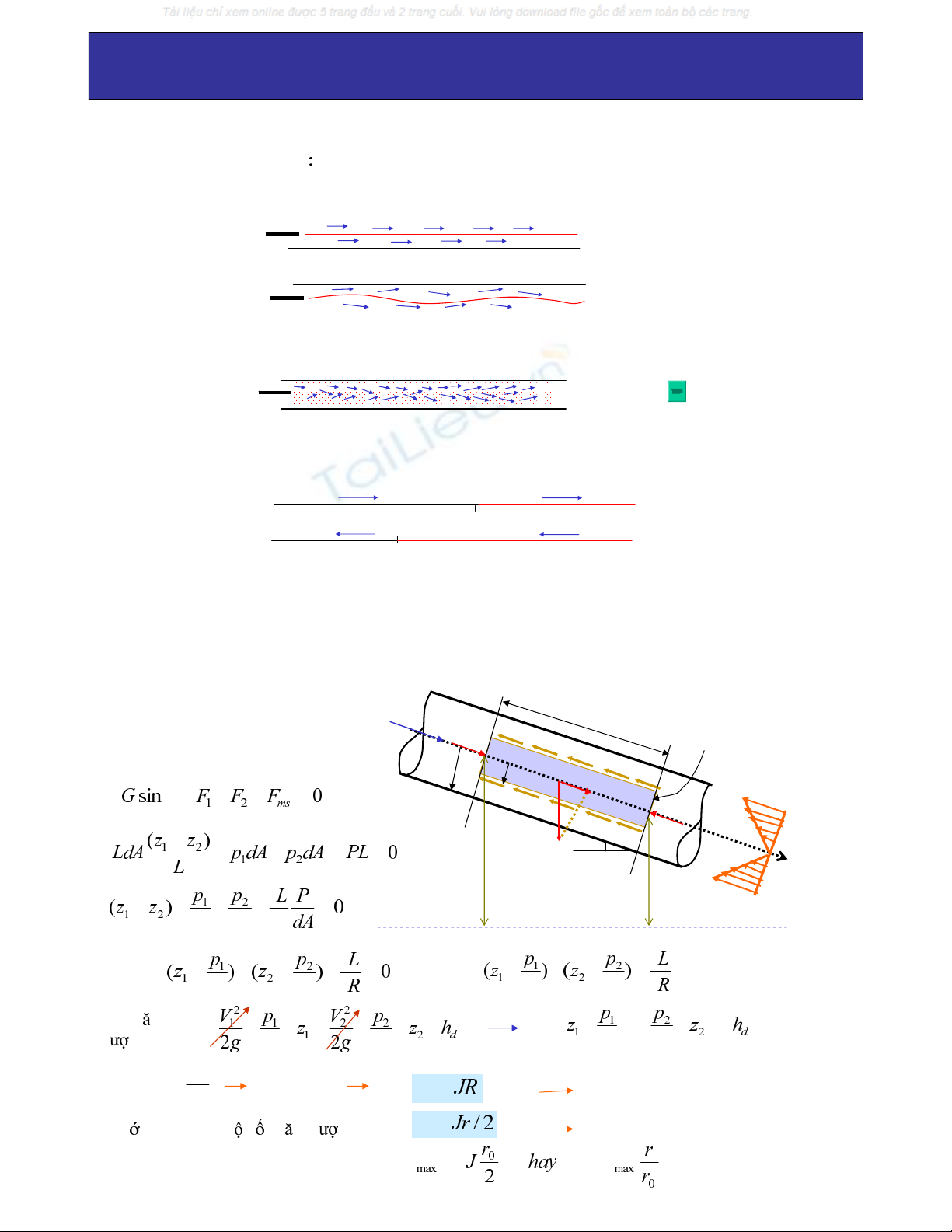Trong oáng xeùt ñoaïn vi phaân doøng chaûy τ = γ ñeàu hình truï coù dieän tích dA nhö hình veõ: V i J = hd / L , đ d c n ng l ng ÖÙùng suaát tieáp tyû leä baäc nhaát theo r PT cô baûn coù theå vieát τ =γ τ =τ Mai Thanh Tròn dh kien truc tphcm
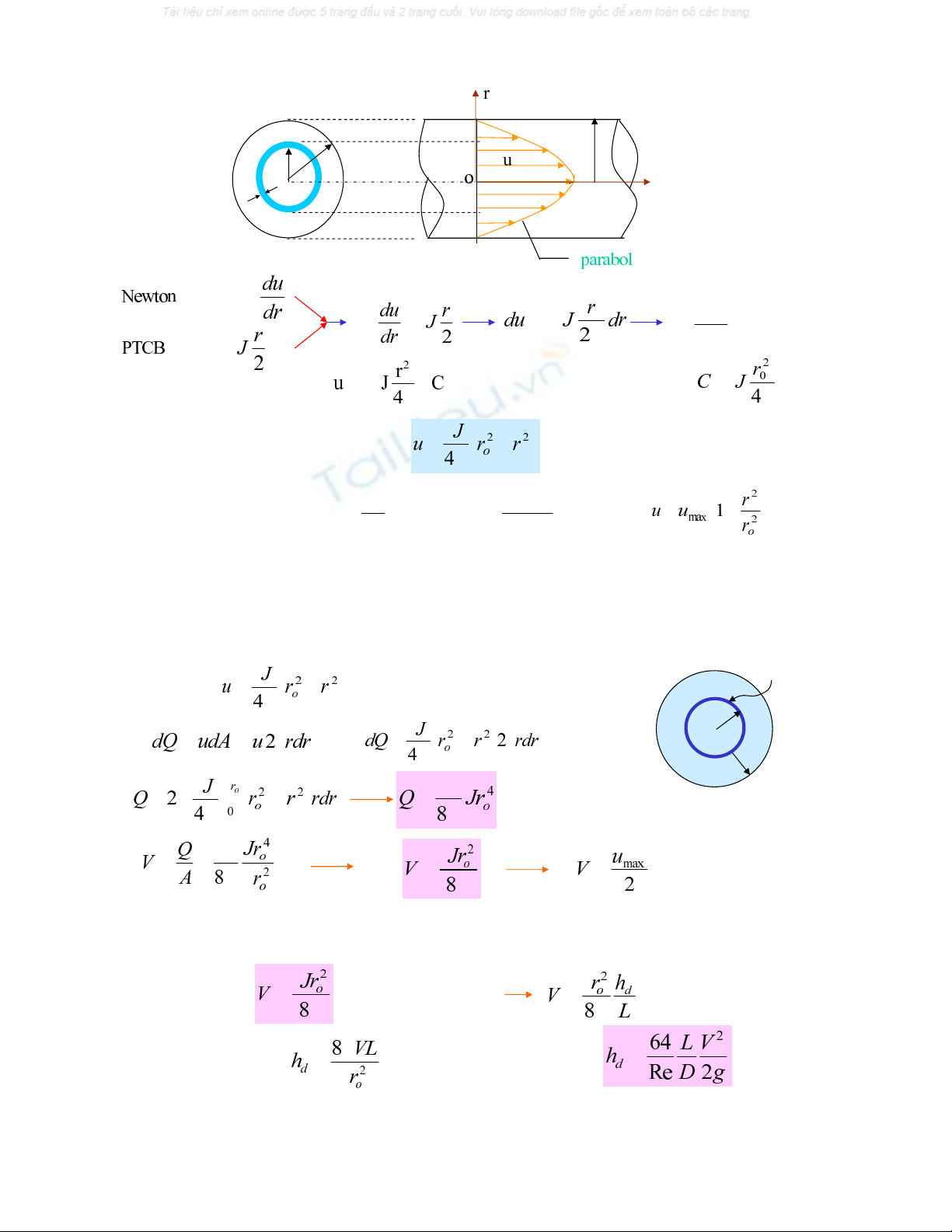
II.PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY TAÀNG r0 r0 r dr τ = −μ = −γ − γJ −μ =γ μ u= 2μ ∫ rdr + C τ =γ = −γ + Taïi r=r0 ta coù u=0, suy ra =γ μ μ γ = μ ( − ) γJ 2 ⎛ r02 − r 2 ⎞ ⎛ ⎞ Taïi r=0 ta coù u=umax umax = r0 ⇒ u = umax ⎜ 2 ⎟ hay = ⎜ − ⎟ ⎜ ⎟ 4μ ⎝ r0 ⎠ ⎝ ⎠ Phaân boá vaän toác trong chaûy taàng coù daïng Parabol · Löu löôïng vaø vaän toác trung bình: γ dA = μ ( − ) γ = = π = μ ( − )π r ro γ πγ = π μ∫ ( − ) = μ πγ γ = = = = μπ μ Toån thaát doïc ñöôøng γ Thay J = hd/L γ Töø = = μ μ Suy ra hd μ saép xeáp laïi = = γ Vôùi Re = VD/ν ( Heä soá Reynolds) Mai Thanh Tròn dh kien truc tphcm
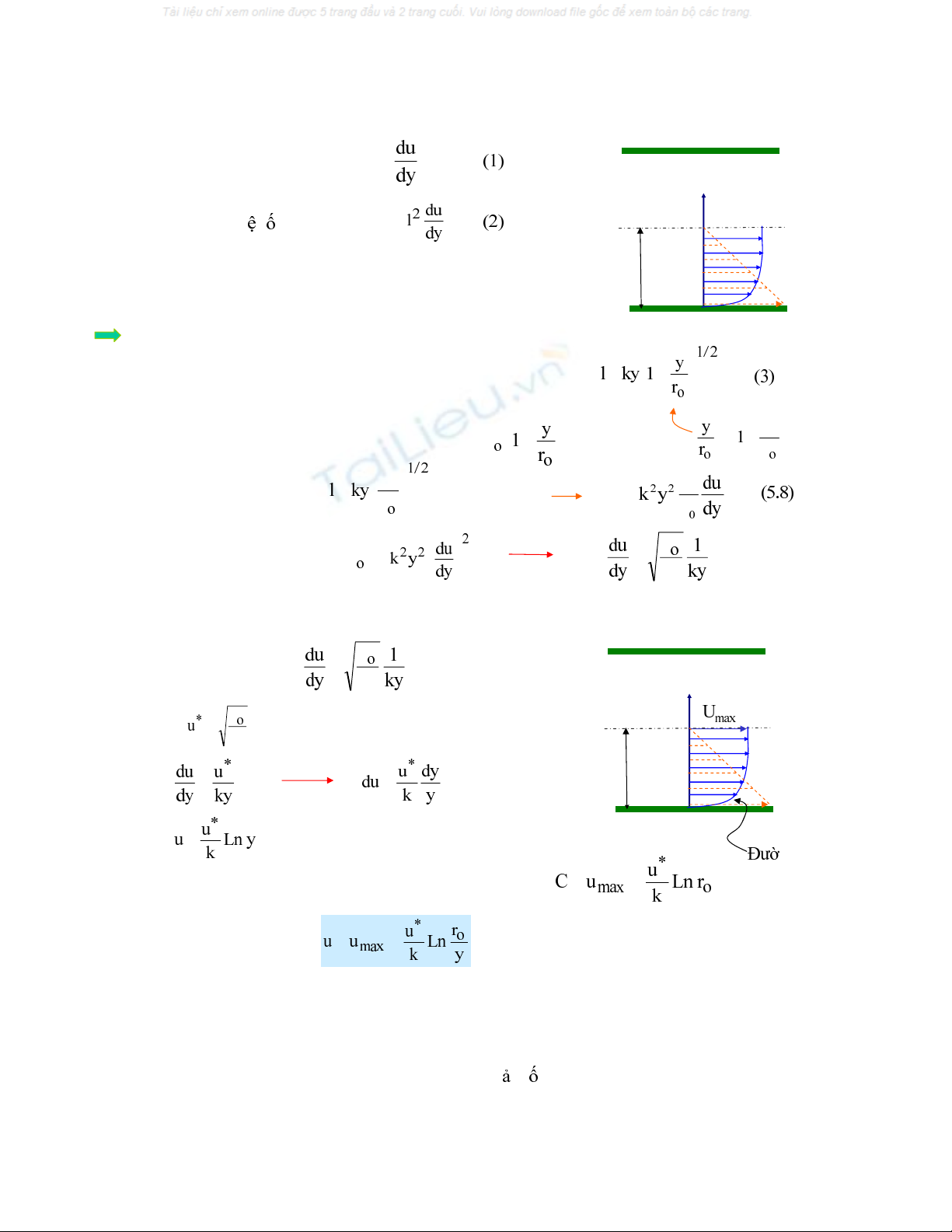
III. PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY ROÁI TRONG OÁNG Ñoái vôùi doøng chaûy roái, öùng suaát tieáp phuï thuoäc chuû yeáu vaøo ñoä chuyeån ñoäng hoãn loaïn cuûa caùc phaân töû löu chaátù. Theo giaû thieát cuûa Prandtl: τ=ε y vôùi ε ñöôïc goïi laø h s nhôùt roái ε=ρ u y : khoaûng caùch töø thaønh ñeán lôùp chaát loûng ñang xeùt ro l :chieàu daøi xaùo troän τo o Prandtl: öùng suaát nhôùt roái khoâng phuï thuoäc vaøo tính nhôùt cuûa löu chaát. ⎛ ⎞ Theo thí nghieäm cuûa Nikudrase, chieàu daøi xaùo troän l trong oáng = ⎜ − ⎟ ⎜ ⎟ ⎝ ⎠ Vôùi k : haèng soá Karman ( k = 0,4) ⎛ ⎞ ⎛ τ ⎞ Neáu xem τ tæ leä tuyeán tính vôùi baùn kính r : τ=τ ⎜ − ⎟ Thì =⎜ − ⎜ ⎟ ⎟ ⎜ ⎟ ⎝ τ ⎠ ⎝ ⎠ Thay vaøo : ⎛ τ ⎞ τ = ⎜ ⎜τ ⎟ ⎟ Töø (2) ε=ρ ⎝ ⎠ τ ⎛ ⎞ τ Thay vaøo (1) : τ =ρ ⎜ ⎜ ⎟ ⎟ = ⎝ ⎠ ρ τ = ρ y τ Ñaët = ρ ( vaän toác ma saùt , m/s) u ro = = τo o = +C ng cong Taïi taâm oáng r = ro u = umax thay vaøo cho = − logarit = − 0 < y ≤ ro Phaân boá löu toác trong tröôøng hôïp chaûy roái coù daïng ñöôøng logarit Do ñoù ta nhaän thaáy söï phaân boá vaân toác trong tröôøng hôïp chaûy roái töông ñoái ñoàng ñeàu gaàn vôùi vaän toác trung bình hôn so vôùi tröôøng hôïp chaûy taàng. Ñoù cuõng laø lyù do taïi sao caùc heä soá söûa chöõa ñoäng naêng (α) hay heä soá söûa chöõa ñoäng löôïng (αo) khi ch y r i coù theå laáy baèng 1 Mai Thanh Tròn dh kien truc tphcm
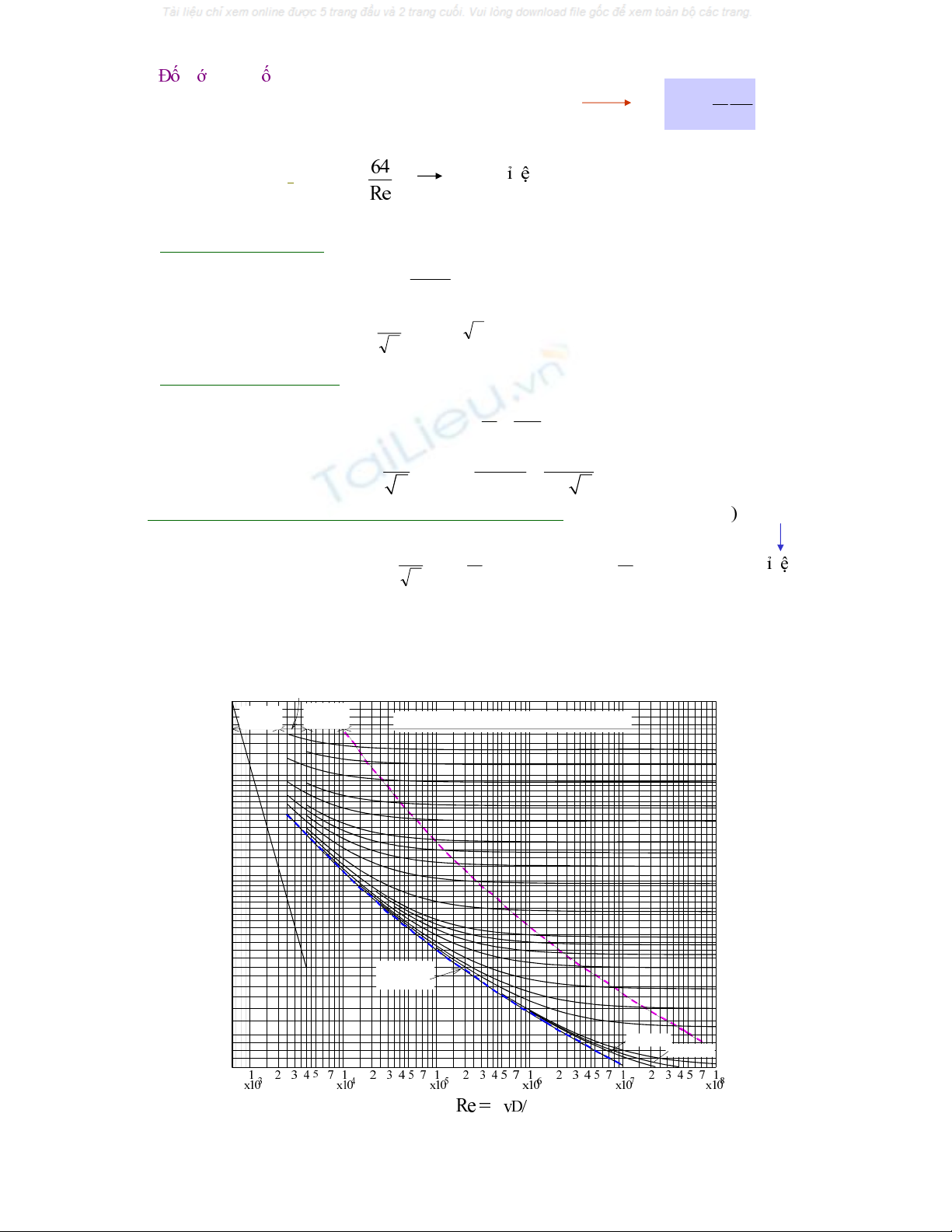
Toån thaát doïc ñöôøng trong doøng chaûy roái: i v i doøng r i töø lyù thuyeát khoâng theå suy ra ñöôïc toån thaát doïc ñöôøng. Duøng phöông phaùp phaân tích thöù nguyeân L V2 hd = λ vaø thí nghieäm chöùng toû ñöôïc toån thaát doïc ñuôøng coù daïng D 2g Xaùc ñònh heä soá toån thaát λ: Doøng chaûy taàng: λ= hd t l V1 Doøng chaûy roái: Roái thaønh trôn thuûy löïc: (2300 < Re < 105 ) λ = f(Re). 0 ,316 Blasius: λ = 1/ 4 Re Prandtl-Nicuradse: 1 λ ( = 2 lg Re λ − 0 ,8 ) Roái thaønh nhaùm thuûy löïc: ( Re > 105 ) λ = f(Re, Δ/D). 0,25 Antersun: ⎛ Δ 100 ⎞ λ = 0,1⎜ 1,46 + ⎟ ⎝ D Re ⎠ Colebrook: 1 ⎛ Δ 2,51 ⎞ = −2 lg ⎜ + ⎟ λ ⎝ 3,71.D Re λ ⎠ Chaûy roái thaønh hoaøn toaøn nhaùm (khu söùc caûn bình phöông) (Re raát lôùn >4.106 λ = f( Δ/D). 1 D ⎛ D⎞ Prandtl-Nicuradse: = 2 lg + 1,14 ≈ 2 lg⎜ 3,17 ⎟ hd t l V2 λ Δ ⎝ Δ⎠ Khu chuyeån tieáp ÑOÀ THÒ MOODY 0,1 Khu chaûy roái Khu 0,09 thaønh nhaùm Khu chaûy roái thaønh nhaùm hoaøn toaøn (Khu söùc caûn bình phöông) Chaûy taàng 0,08 0,07 0,05 0,04 0,06 0.03 0,05 0,02 0,015 0,04 0,01 λ 0,008 0,006 0,004 _ 0,03 0,025 Δ=Δ/D 0,002 0,02 0,001 0,000 6 Khu chaûy roái 0,000 4 0,015 thaønh trôn 0,000 2 0,000 1 0,000 05 0,01 0,000 005 0,009 0,000 007 0,008 0,000 01 ρ μ Mai Thanh Tròn dh kien truc tphcm
III. TÍNH TOAÙN TOÅN THAÁT CUÛA DOØNG CHAÛY TRONG OÁNG 1.Toån thaát ñöôøng daøi: Coâng thöùc tính toån thaát doïc ñuôøng coù daïng L V2 (Darcy) λ = f(Re, Δ/D) : heä soá toån thaát hd = λ D 2g Δ : Heä soá nhaùm tuyeät ñoái (chieàu cao caùc moá nhaùm ) thay D = 4R = λ vôùi J = hd/L = vaø ñaët = ( heä soá Chezy) λ λ = ( Coâng thöùc Chezy) löu löôïng = = Vôùi module löu löôïng = Heä soá Chezy C coù theå tính theo coâng thöùc Manning : = ( n laø ñoä nhaùm Coâng thöùc Manning chæ duøng khi doø chaûy roái thaønh hoaøn toaøn nhaùm T coâng thöù tính löu löôïng = = = 3.Toån thaát cuïc boä: Tính theo coâng thöùc thöïc nghieäm Weisbach: V ξ laø heä soá toån thaát cuïc boä (phuï thuoäc vaøo töøng daïng toån thaát) h c = ξc g V laø vaän toác doøng chaûy taïi vò trí sau khi xaûy ra toån thaát Môû roäng ñoät ngoät ⎛ ⎞ V1 V2 ξ =⎜ − ⎜ ⎟ ⎟ vôùi V1 ⎝ ⎠ A1 ⎛ ⎞ vôùi V2 A2 ξ =⎜ ⎜ − ⎟ ⎟ ⎝ ⎠ Hai coâng thöùc treân ñöôïc chöùng minh töø lyù thuyeát ÔÛ mieäng ra cuûa oáng: ξc=1 ÔÛ mieäng vaøo cuûa oáng: ξc=0,5 Mai Thanh Tròn dh kien truc tphcm
IV. CAÙC BAØI TOAÙN TRONG ÑÖÔØNG OÁNG 1. Phaân bieät ñöôøng oáng daøi, ngaén hc5%hd : oáng ngaén h f = hd + hc 2. Ñöôøng oáng maéc noái tieáp A A Maët chuaån B B h l1; d1; λ1 l2; d2; λ2 V1 V2 l3; d3; λ3 V3 VA2 p A V2 p + + zA = B + B + zB + h fA − B 2g γ 2g γ ⎛ ⎞ ⎛ ⎞ = ⎜λ ⎜ +λ +λ ⎟ + ⎜ξ ⎟ ⎜ +ξ +ξ +ξ ⎟ ⎟ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ = ⎜λ ⎜ +λ +λ +ξ +ξ +ξ +ξ ⎟ ⎟ ⎝ ⎠ Trong ñoù A1, A2 , A3 laø tieát dieän oáng 1, 2, vaø 3. Q chaûy trong oáng neáu bieát caùc thoâng soá coøn laïi 3. Ñöôøng oáng maéc song song (boû qua toån thaát cuïc boä). Q1? Q Q2? Q3 ? Goïi HA vaø HB laø naêng löôïng taïi A vaø B. Neáu xeùt doøng chaûy ñi töø A ñeán B treân oáng 1 , ta coù toån thaát treân oáng soá 1 laø : Töông töï, xeùt doøng chaûy töø A ñeán B treân oáng 2 vaø 3 toån thaát oáng 2 vaø 3 laø : Nhö vaäy Neáu boû qua toån thaát cuïc boä : = = = (i) = (ii) vaø (iii) Töø 3 phöông trình (i), (ii), (iii) Q1, Q2 vaø Q3 Mai Thanh Tròn dh kien truc tphcm
4. Ñöôøng oáng noái 3 hoà chöùa (boû qua toån thaát cuïc boä). Ñöôøng naêng Ñöôøng naêng gæa söû Hj Hj 1 Hj 2 Z2 l1; d1; n1 l2; d2; n2 Z1 J Maët chuaån l3; d3; n3 3 Ñöôøng naêng Chaûy töø J veà 2 Chaûy töø 2 veà J Khoâng chaûy treân oáng 2 Caùch xaùc ñònh chieàu doøng chaûy treân oáng 2 Ñöôøng naêng gæa söû Hj 1 2 Z2 l1; d1; n1 l2; d2; n2 Z1 J Maët chuaån l3; d3; n3 Giaû söû cao trình naêng löôïng taïi J , 3 Hj ngang vôùi möïc nöôùc trong boàn 2 − = − = = Toån thaát treân oáng 1 Toån thaát treân oáng 2 = = Toån thaát treân oáng 3 = = = Q1 > Q3 => trong oáng 2 doøng chaûy ñi töø J veà boàn 2 Q1 < Q3 => trong oáng 2 doøng chaûy ñi töø boàn 2 veà J Q1 = Q3 => trong oáng 2 khoâng coù doøng chaûy Mai Thanh Tròn dh kien truc tphcm
Hj 1 2 Z2 l1; d1; n1 l2; d2; n2 Q1 Z1 Q2 J Maët chuaån Q3 l3; d3; n3 3 Thí duï tröôøng hôïp 1 xaûy ra, Q1 > Q3 − Toån thaát treân oáng 1 : − = = − Toån thaát treân oáng 2 − = = Toån thaát treân oáng 3 = = 5. Maïng ñöôøng oáng kín: Löu löôïng trong töøng oáng ñöôïc xaùc ñònh döïa vaøo 2 ñieàu kieän cuûa doøng chaûy trong maïng kín nh sau 1. Taïi moät nuùt löu löôïng ñeán phaûi baèng löu löôïng ñi 2. Trong moät voøng kín, toång toån thaát phaûi baèng khoâng Qui öôùc doøng chaûy theo chieàu tính toùan toån thaát laáy daáu döông (+) vaø doøng chaûy ngöôïc chieàu tính toùan toån thaát laáy daáu aâm (-) Böôùc tính toaùn Böôùc 1: Töï phaân phoái löu löôïng treân töøng oáng sao cho thoûa maõn ñieàu kieän 1 Böôùc 2: Ñieàu chænh laïi löu löôïng töøng oáng sao cho thoûa maõn ñieàu kieän 2 AÙp duïng phöông phaùp Hardy Cross Mai Thanh Tròn dh kien truc tphcm m
Phöông phaùp Hardy Cross AÙp duïng cho nhöõng coâng thöùc tính toån thaát doïc döôøng coù daïng Thí duï = Goïi Qi laø löu löôïng töï phaân phoái ñöôïc treân oáng i ( chöa thoûa maõn ñieàu kieän 2) ΔQ laø löu löôïng caàn ñieàu chænh trong moät voøng ñeå thoûa maõn ñieàu kieän 2 Toån thaát naêng löôïng treân oáng i khi ñaõ ñieàu chænh laø hdi = mi (Qi +ΔQ)x hdi = mi (Qi x +xΔQ Qx-1 + …….) Gaàn ñuùng hdi = mi (Qi x +xΔQ Qx-1) Trong moät voøng kín, toång toån thaát phaûi baèng khoâng ∑ ( + Δ − ) = vôùi k laø soá oáng trong moät voøng = ∑= + Δ ∑ = − = k ∑mQ i i x ΔQ = − i =1 k x ∑ mi Qix −1 i =1