Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
151
KHẢO SÁT VÀ TÍNH TOÁN THAM SỐ BỘ ĐIỀU KHIỂN
DỰ BÁO MPC CHO THÁP CHƯNG CẤT
Phan Thanh Tùng1, Bùi Văn Đại 2
1Đại học Thủy lợi, email: phanthanhtung86@gmail.com
2Đại học Thủy lợi, email: buidai68@gmail.com
1. GIỚI THIỆU CHUNG
Mô hình tháp chưng cất là bài toán điển
hình của hệ thống nhiều vào nhiều ra có liên
kết nội. Hiện nay có rất nhiều phương pháp
thiết kế bộ điều khiển như PID tách kênh,
mờ, noron,… nhưng chúng chỉ quan tâm đến
đầu ra mà bỏ qua đánh giá về tín hiệu điều
khiển. Các vấn đề điều khiển trong công
nghiệp cũng rất cần tối ưu về nhiều mặt như:
tối ưu năng lượng tín hiệu điều khiển, thời
gian trích mẫu, giá thành… Do đó cần có bộ
điều khiển đáp ứng yêu cầu trên.
Bộ điều khiển dự báo MPC ra đời đã được
đông đảo các kỹ sư công nghệ đón nhận. Với
việc dễ hiểu, dễ cài đặt cùng với chất lượng
điều khiển tốt, tối ưu hóa năng lượng giúp
giải quyết rất nhiều bài toán công nghiệp.
Phương pháp MPC giải bài toán tối ưu đồng
thời cho cả sai lệch đầu ra và năng lượng
điều khiển thông qua trọng số λ nên nâng cao
chất lượng đầu ra.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Bằng việc nghiên cứu khảo sát từng thành
phần, từng tham số của bộ điều khiển cùng
với yêu cầu bài toán đặt ra về tối ưu năng
lượng, ta sẽ thu được bộ điều khiển dự báo
mong muốn.
Hình 1: Mô tả ví dụ phương pháp MPC
Xét mô hình rời rạc của tháp chưng cất:
x(t+ 1) = Adx(t) + Bdu(t) + Edd(t)
y(t + 1) = Cdx(t + 1)
Trong đó:
0,1803 0,184 0,164
0,449 0,461 0,415
0,167 0,174 0,173
d





A
,
1 0 0
0 0 1
d



C
0,187 0,0401
0,4218 0,0008
0,1137 0,0021
d





B
,
0,1065 0,2016
0,1976 0,5604
0,0524 0,1532
d





E
Với: T = [x1, x2, x3] là vector 3 biến
trạng thái
uT = [u1, u2] là vector 2 đầu vào điều khiển
dT = [d1, d2] là vector 2 nhiễu loạn.
yT = [y1, y2] là vector 2 biến đầu ra.
Bước 1: Để có thể tối ưu hóa được sự biến
thiên năng lượng tín hiệu điều khiển thì
chuyển mô hình thành:
( 1) ( )
( 1) ( )
( ) ( 1)
dd
z t z t
Az
tt
tt



AB
xx
uu
0I
( ) ( )
dd
BE
zz
tt
BE
ud
I0
( 1)
( 1)
( 1) ()
d
Czzt
xt
yt ut

 

0C
Với:
z(t + 1)T = [x(t +1) ; u(t)] là vector trạng
thái mới.
u(t) = u(t) – u(t – 1) là chênh lệch năng
lượng điều khiển.
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
152
Bước 2: Tính các ma trận Pz, Py, Hz, Hy
𝑧(𝑡+1)
𝑧(𝑡+2)
…
𝑧(𝑡+𝑁𝑦)
=
⏟
𝑍
𝐴𝑧
𝐴𝑧
2
…
𝐴𝑧𝑁𝑦
⏟
𝑃𝑧
𝑧(𝑡) +
+
𝐵𝑧
𝐴𝑧𝐵𝑧
…
𝐴𝑧
𝑁𝑦−1𝐵𝑧 0
𝐵𝑧
…
𝐴𝑧
𝑁𝑦−2𝐵𝑧 ⋱ 0
0
…
𝐴𝑧𝑁𝑦−𝑁𝑢𝐵𝑧
⏟
𝐻𝑧[∆𝑢(𝑡)
∆𝑢(𝑡+1)
…
∆𝑢(𝑡+𝑁𝑢−1)]
⏟
∆𝑈
𝑦(𝑡+1)
𝑦(𝑡+2)
…
𝑦(𝑡+𝑁𝑦)
⏟
=
𝑌
𝐶𝑧𝐴𝑧
𝐶𝑧𝐴𝑧
2
…
𝐶𝑧𝐴𝑧
𝑁𝑦
⏟
𝑃𝑦
𝑧(𝑡)+
+
𝐶𝑧𝐵𝑧
𝐶𝑧𝐴𝑧𝐵𝑧
…
𝐶𝑧𝐴𝑧
𝑁𝑦−1𝐵𝑧 𝐶𝑧0
𝐵𝑧
…
𝐶𝑧𝐴𝑧
𝑁𝑦−2𝐵𝑧 ⋱ 0
0
…
𝐶𝑧𝐴𝑧𝑁𝑦−𝑁𝑢𝐵𝑧
[∆𝑢(𝑡)
∆𝑢(𝑡+1)
…
∆𝑢(𝑡+𝑁𝑢−1)]
⏟
Viết gọn lại:
𝑍󰆹=𝑃𝑧𝑧(𝑡)+𝐻𝑧∆𝑈
𝑌=𝑃𝑦𝑧(𝑡)+𝐻𝑦∆𝑈
trong đó: NY là tầm dự báo kết quả đầu ra.
Nu là tầm điều khiển.
Bước 3: Thiết lập hàm mục tiêu:
𝐽=‖𝑅−𝑃𝑦𝑧(𝑡)−𝐻𝑦∆𝑈‖2
2+𝜆‖∆𝑈‖2
2.
Ở đây: R là vector giá trị đặt mong muốn
λ là biến trọng số thể hiện tầm
quan trọng tối ưu năng lượng trong
hàm mục tiêu.
J là hàm mục tiêu can tối thiểu.
Hay: ∆𝑈=(𝐻𝑦𝑇𝐻𝑦+𝜆𝐼)−1𝐻𝑦𝑇(𝑟−𝑃𝑦𝑧(𝑡))
Ký hiệu Pr là ma trận con chứa p hàng đầu
tiên của (𝐻𝑦𝑇𝐻𝑦+𝜆𝐼)−1𝐻𝑦𝑇;
Luật điều khiển cho thời điểm t đó là:
Δu(t) = Pr . (r –Py. z(t)) = Pr .r – Kz .z(t)
Trong đó: Ts: Thời gian trích mẫu,
r1, r2: Giá trị dặt cho đầu vào 1 và 2.
Khảo sát tham số thời gian trích mẫu:
Trước hết ta sẽ thay đổi thời gian trích
mẫu Ts để thu được đặc tính động học của hệ
thống ở mức độ chấp nhận được.
Nhận xét : Khi ta chọn chu kì trích mẫu Ts
càng nhỏ hệ càng nhanh chóng bám giá trị
đặt và có thời gian quá độ rất ngắn (với
Ts=0,1s thời gian quá độ chưa đến 2s). Điều
này hoàn toàn dễ hiểu vì trong cùng một
khoảng thời gian thì khi Ts nhỏ thì càng phải
tính toán nhiều lần và thay đổi tín hiệu đầu
vào U1 nhiều lần hơn so với Ts lớn. Điều đó
dẫn đến giá trị U1 tăng đột biến đảm bảo
nhanh chóng đưa hệ bám sát giá trị đặt.
Vì vậy muốn nhanh bám giá trị đặt thì ta
phải trả giá bằng khối lượng tính toán lớn,
nhanh chóng và đặc biệt quan trọng là tín hiệu
điều khiển tăng rất lớn có thể vượt ngưỡng cho
phép. Do đó ta phải thỏa hiệp ở 2 điều này.
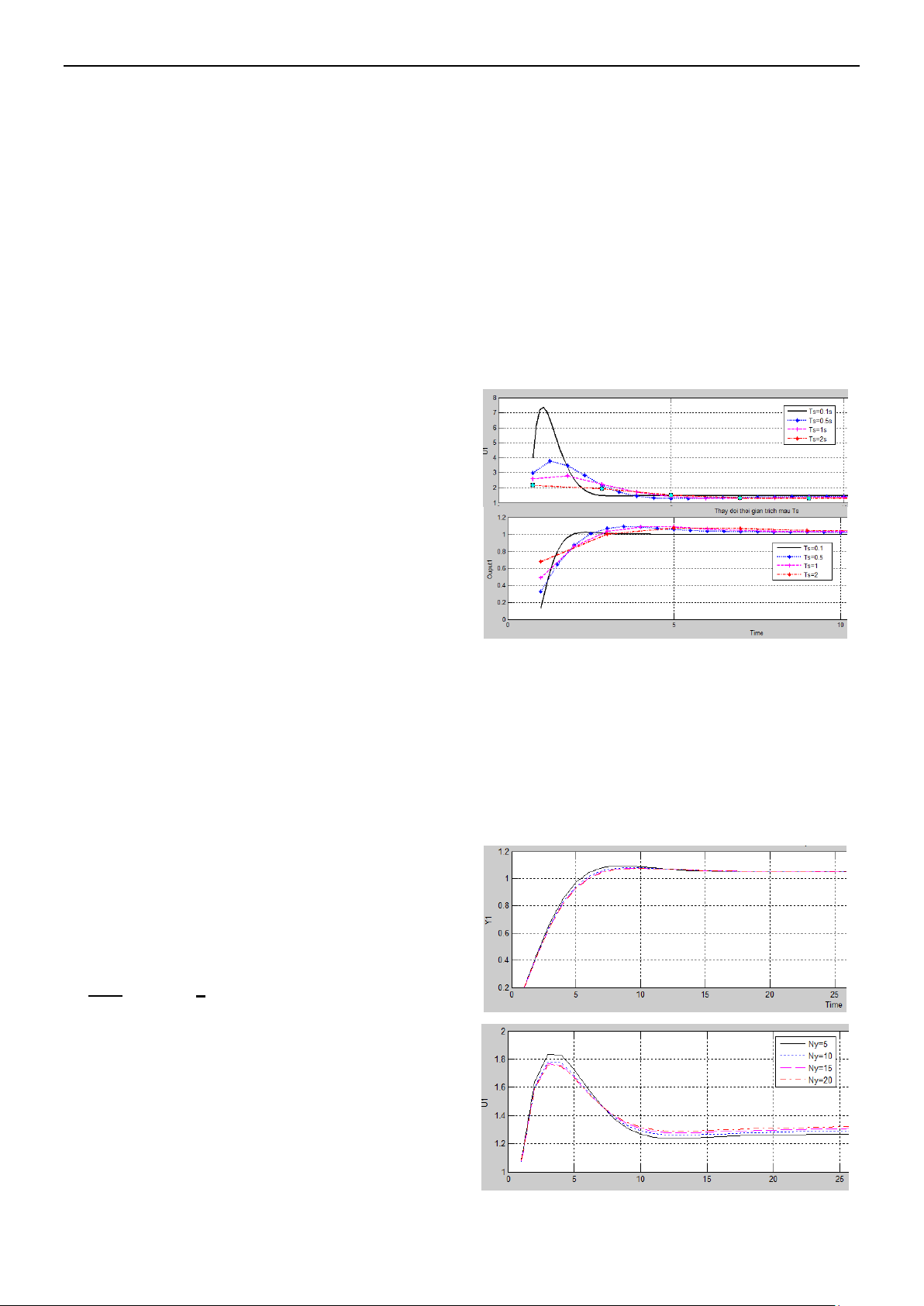
Hình 2: Đáp ứng hệ thống khi thay đổi Ts.
Chọn chu kì trích mẫu Ts hợp lí để tín hiệu
điều khiển U không quá lớn và ta chọn Ts=1s
khiến cho khối lượng tính toán trở nên nhẹ
nhàng và biên độ đầu vào không quá lớn.
Thay đổi tầm dự báo Ny với Ts=1s, Nu=5,
1
;
Hình 3: Đáp ứng hệ thống khi thay đổi Ny.
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
153
Nhận xét: Qua hình vẽ ta thấy khi Ny>5
thì gần như tất cả các quỹ đạo của hệ và tín
hiệu điều khiển tương tự như nhau và ta nên
chọn Ny=10 để giảm khối lượng tính toán
của vi xử lí.
Thay đổi Nu với Ts=1, Ny =10,
0,1
;
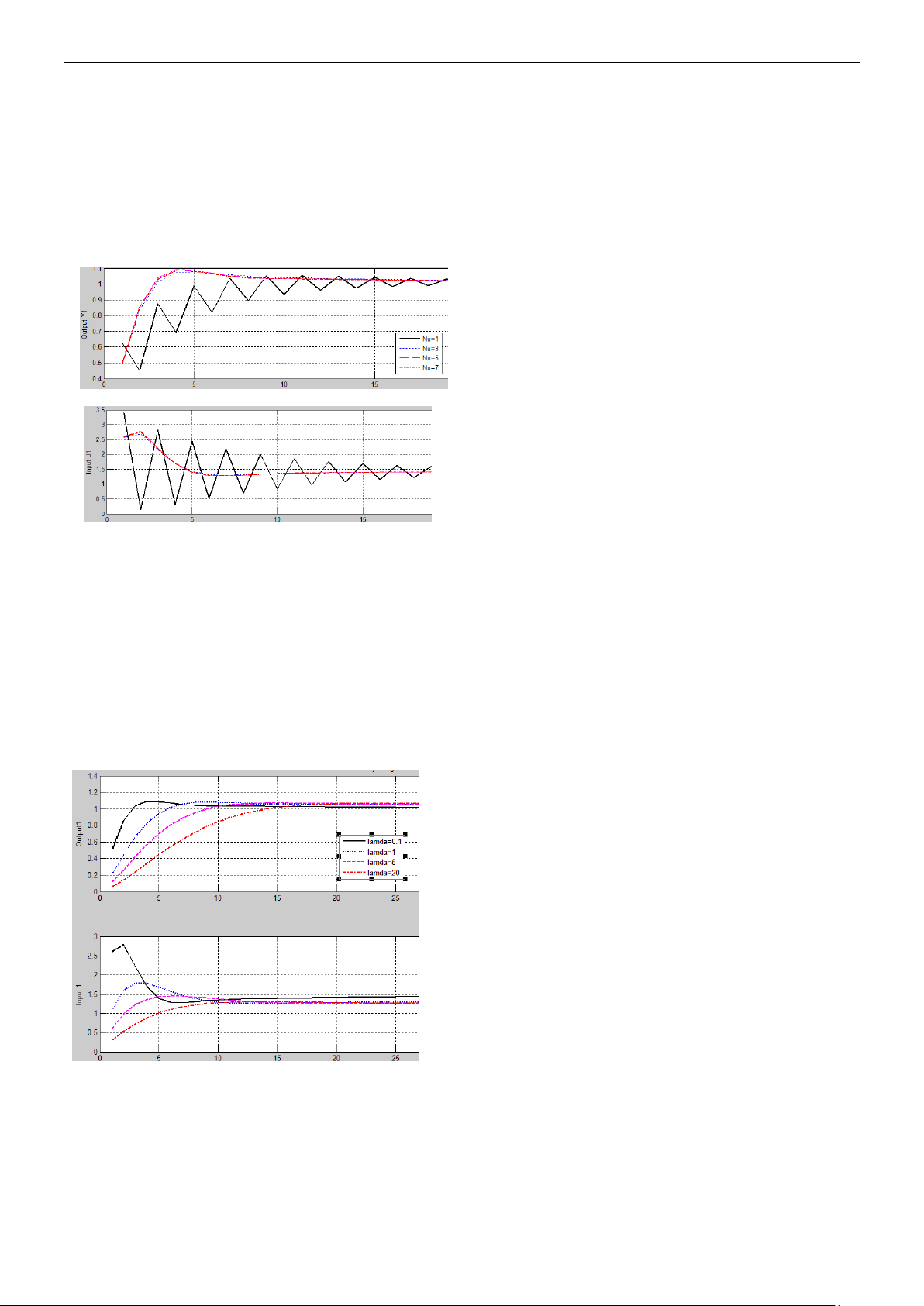
Hình 4. Thay đổi Nu
Nhận xét: Khi Nu > 3 thì đáp ứng đầu ra
giống như nhau và tín hiệu điều khiển có độ
lớn vừa phải tạm chấp nhận được
Khi Nu=1 (tầm điều khiển ngắn tương tự
deadbeat) khiến tín hiệu điều khiển lớn và có
biên độ dao động cao
Thay đổi lamda λ
.
Hình 5: Ảnh hưởng của trọng số lamda
tính toán.
Nhận xét: Ta thấy lamda càng nhỏ thì hệ
thống đáp ứng càng nhanh, càng bám giá trị
đặt nhưng ta phải trả giá tín hiệu điều khiển
ban đầu lại lớn và thay đổi nhiều. Điều này
dễ hiểu vì tín hiệu điều khiển lớn thì hệ mới
nhanh chóng bám giá trị đặt và do bị đánh giá
thấp trong hàm mục tiêu khi lamda nhỏ nên
nó có biến động lớn.
3. SO SÁNH VÀ ĐÁNH GIÁ KẾT QUẢ
Khi Ts càng nhỏ thì hệ đáp ứng càng nhanh,
sai lệch tĩnh ít nhưng tín hiệu điều khiển U tăng
rất lớn và đòi hỏi tính toán nhiều.
Khi Nu =1 thì hệ dao động nhiều, với Nu
>3 thì các đặc tính của hệ là tương tự nhau.
Khi Ny > 5 thì đặc tính hệ là tương đồng, để
đảm bảo ổn định thì chọn Ny > Nu. Chọn Nu,
Ny càng lớn thì khối lượng tính toán càng lớn.
Khi lamda ( càng nhỏ thì sai lệch tĩnh
càng ít, hệ càng nhanh chóng bám giá trị đặt,
khi lamda lớn thì hệ đáp ứng chậm và sai lệch
tĩnh càng rõ (vì hệ không có phản hồi đầu ra
nên ta có thể thêm một khâu tích phân PI).
4. KẾT LUẬN VÀ KIếN NGHỊ
Với phương pháp điều khiển dự báo MPC
giúp cho việc tính toán tối ưu năng lượng tiêu
thụ cho hệ thống dễ dàng hơn. Bộ điều khiển
dự báo mang lại lợi thế to lớn trong việc điều
khiển các quá trình công nghiệp mà ở đó các
bộ điều khiển khác không đáp ứng được
yêu cầu.
5. TÀI LIỆU THAM KHẢO
[1] Hoàng Minh Sơn: Cơ sở hệ thống điều khiển
quá trình, NXB Khoa học và Kỹ thuật, 2006
[2] Rossiter: Model based Predictive Control -
Prentice Hall, 2009.
[2] Nguyễn Doãn Phước, Phan Xuân Minh: Lý
thuyết điều khiển tuyến tính, NXB Khoa học
và Kỹ thuật, 2003.
[3] Robert H. Bishop: Modern Control System,
Prentice Hall, 2012.