
KÌ THI TH Đ I H C, CAO Đ NG Ử Ạ Ọ Ẳ
NĂM H C 2009 – 2010Ọ
MÔN: TOÁN, KH I A,BỐ
Th i gian làm bài 180 phút không k th i gian phát đờ ể ờ ề
I. PH N CHUNG CHO T T C THÍ SINHẦ Ấ Ả
Câu I( 2,0 đi m): Cho hàm s : ể ố (C)
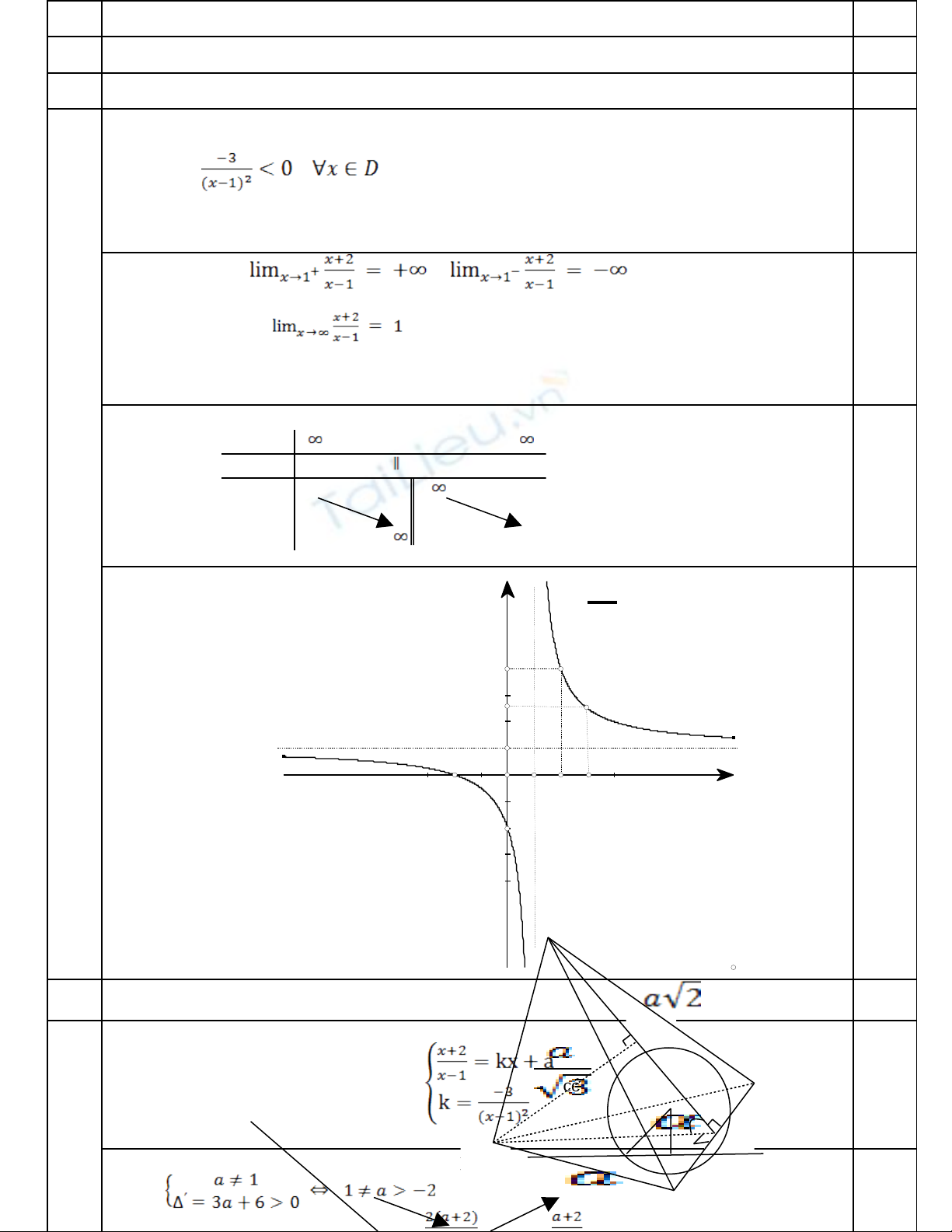
1. Kh o sát và v đ th (C) hàm s ả ẽ ồ ị ố
2. Cho đi m A( 0; a) Tìm a đ t A k đ c 2 ti p tuy n t i đ th (C) sao cho 2 ti p đi m t ng ngể ể ừ ẻ ượ ế ế ớ ồ ị ế ể ươ ứ
n m v 2 phía c a tr c hoành.ằ ề ủ ụ
Câu II (2,0 đi m): ể
1. Gi i ph ng trình l ng giác.ả ươ ượ
2. Gi i h ph ng trình.ả ệ ươ
Câu III(1,0 đi m): Tính tích phân sau.ể
∫
=
3
4
42
cos.sin
π
π
xx
dx
I
Câu IV(1,0 đi m): Cho ba s th c ể ố ự th a mãn ỏ ,Ch ng minh r ng:ứ ằ
Câu V(1,0 đi m): Cho t di n ABCD có AC = AD = ể ứ ệ , BC = BD = a, kho ng cách t B đ n m t ph ngả ừ ế ặ ẳ
(ACD) b ng ằ . Tính góc gi a hai m t ph ng (ACD) và (BCD). Bi t th c a kh i t di n ABCD b ng ữ ặ ẳ ế ể ủ ố ứ ệ ằ .
II. PH N RIÊNG (Thí sinh ch đ c làm 1 trong 2 ph n A ho c B)Ầ ỉ ượ ầ ặ
A. Theo ch ng trình chu n.ươ ẩ
Câu VIa(2,0 đi m):ể
1. Trong không gian v i h t a đ Oxyz cho 4 đi m : A(1;2; 2) B(-1;2;-1) C(1;6;-1) D(-1;6;2). Tìm t a đớ ệ ọ ộ ể ọ ộ
hình chi u vuông góc c a đi m A trên m t ph ng (BCD)ế ủ ể ặ ẳ
2. Trong mp v i h t a đ Oxy cho đ ng tròn : xớ ệ ọ ộ ườ 2 +y2 -2x +6y -15=0 (C ).
Vi t PT đ ng th ng (Δ) vuông góc v i đ ng th ng : 4x-3y+2 =0 và c t đ ng tròn (C) t i A; B ế ườ ẳ ớ ườ ẳ ắ ườ ạ
sao cho AB = 6
Câu VIIa(1,0 đi m): Xác đ nh h s c a xể ị ệ ố ủ 5 trong khai tri n (2+x +3xể2 )15
B. Theo ch ng trình nâng cao.ươ
Câu VIb(2,0 đi m):ể
1. Trong không gian v i h t a đ Oxyz cho 4 đi m : A(1;2; 2) B(-1;2;-1) C(1;6;-1) D(-1;6;2). Tìm t a đớ ệ ọ ộ ể ọ ộ
hình chi u vuông góc c a đi m A trên m t ph ng (BCD)ế ủ ể ặ ẳ
2. Trong mp v i h t a đ Oxy cho đ ng tròn : xớ ệ ọ ộ ườ 2 +y2 -2x +6y -15=0 (C ).
Vi t PT đ ng th ng (Δ ) vuông góc v i đ ng th ng : 4x-3y+2 =0 và c t đ ng tròn (C) t i A; B ế ườ ẳ ớ ườ ẳ ắ ườ ạ
sao cho AB = 6
Câu VIIb(1,0 đi m):Gi i ph ng trình:ể ả ươ
-------------------------------------------- H T------------------------------------------------Ế

Cán b coi thi không gi i thích gì thêm.ộ ả

(H ng d n và bi u đi m ch m g m 06 trang)ướ ẫ ể ể ấ ồ
Môn: TOÁN: KH I A,BỐ
CÂU N I DUNGỘĐI MỂ
I 2,0
1 1,0
•TXĐ: D= R\{1}
•y’=
Hàm s luông ngh ch bi n trên D và không có c c trố ị ế ự ị
0,25
•Gi i h n: ớ ạ
•PT đ ng TCĐ: x=1; PT đ ng TCN: y=1ườ ườ
0,25
•B ng biên thiên: ả
t - 1 +
f’(t) - +
f(t)
1 +
- 1
0,25
•Đ th :ồ ị 0,25
2 1,0
•G i k là h s góc c a đt đi qua A(0;a). ọ ệ ố ủ PT đt d có d ng y= kx+a (d)ạ
•d là ti p tuy n v i ( C ) ế ế ớ ⇔ h PT ệ có nghi mệ
<=>Pt (1-a)x2 +2(a+2)x-(a+2)=0 (1) có nghi m x ≠ 1ệ
0,25
•Theo bài ra qua A có 2 ti p tuy n thì pt (1) có 2 nghi m xế ế ệ 1 ; x2 phân bi tệ
Đk là : (*)
•Khi đó theo Viet ta có : x1 +x2 = ; x1.x2 =
0,25
H
D
E
C
B
A
x
y
f
x
( )
=
x+2
x-1
1
4
-2
-2
O
1
2
3
5/2
I
A H B
















![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




