http://ductam_tp.violet.vn/
Đ THI TH Đ I H C L N 2 - NĂM H C 2011Ề Ử Ạ Ọ Ầ Ọ
Môn: TOÁN (Th i gian : 180 phút)ờ
PH N CHUNG CHO T T C CÁC THÍ SINHẦ Ấ Ả
Câu I (2 đi m):ể
1).Kh o sát s bi n thiên và v đ th (C) c a hàm s : ả ự ế ẽ ồ ị ủ ố
3x 4
yx 2
−
=−
. Tìm đi m thu c (C) cáchể ộ
đ u 2 đ ng ti m c n .ề ườ ệ ậ
2).Tìm các giá tr c a m đ ph ng trình sau có 2 nghi m trên đo n ị ủ ể ươ ệ ạ
2
0; 3
π
.
sin6x + cos6x = m ( sin4x + cos4x )
Câu II (2 đi m):ể
1).Tìm các nghi m trên ệ
( )
0;2
π
c a ph ng trình : ủ ươ
sin 3x sin x sin 2x cos2x
1 cos2x
−= +
−
2).Gi i ph ng trìnhả ươ :
3 3
x 34 x 3 1
+ − − =
Câu III (1 đi m):ểCho chóp S.ABC có đáy ABC là tam giác vuông t i C, AC = 2, BC = 4. C nh bênạ ạ
SA = 5 vuông góc v i đáy. G i D là trung đi m c nh AB.ớ ọ ể ạ
1).Tính góc gi a AC và SD;ữ2).Tính kho ng cách gi a BC và SD.ả ữ
Câu IV (2 đi m):ể
1).Tính tích phân: I =
2
0
sin x cosx 1 dx
sin x 2cosx 3
π
− +
+ +
∫
2). a.Gi i ph ng trình sau trên t p s ph c C : | z | - iz = 1 – 2iả ươ ậ ố ứ
b.Hãy xác đ nh t p h p các đi m trong m t ph ng ph c bi u di n các s ph c z tho mãn :ị ậ ợ ể ặ ẳ ứ ể ễ ố ứ ả
1 < | z – 1 | < 2
PH N T CH N: Thí sinh ch n câu V.a ho c câu V.b Ầ Ự Ọ ọ ặ
Câu V.a.( 2 đi m ) Theo ch ng trình Chu nể ươ ẩ
1).Vi t ph ng trình các c nh c a tam giác ABC bi t B(2; -1), đ ng cao và đ ng phân giácế ươ ạ ủ ế ườ ườ
trong qua đ nh A, C l n l t là : (dỉ ầ ượ 1) : 3x – 4y + 27 = 0 và (d2) : x + 2y – 5 = 0
2). Trong không gian v i h t a đ Oxyz, cho các đ ng th ng:ớ ệ ọ ộ ườ ẳ
( )
1
x 1
d : y 4 2t
z 3 t
=
= − +
= +
và
a. Ch ng minh r ng (ứ ằ d1) và (d2) chéo nhau.
b. Vi t ph ng trình m t c u (S) có đ ng kính là đo n vuông góc chung c a (ế ươ ặ ầ ườ ạ ủ d1) và (d2).
3). M t h p ch a 30 bi tr ng, 7 bi đ và 15 bi xanh . M t h p khác ch a 10 bi tr ng, 6 bi đ vàộ ộ ứ ắ ỏ ộ ộ ứ ắ ỏ
9 bi xanh . L y ng u nhiên t m i h p bi m t viên bi . Tìm xác su t đ 2 bi l y ra cùng màu .ấ ẫ ừ ỗ ộ ộ ấ ể ấ
Câu V.b.( 2 đi m ) Theo ch ng trình Nâng caoể ươ
1).Trong m t ph ng v i h t a đ Đ các vuông góc Oxy , xét tam giác ABC vuông t i A,ặ ẳ ớ ệ ọ ộ ề ạ
ph ng trình đ ng th ng BC là : ươ ườ ẳ
3
x – y -
3
= 0, các đ nh A và B thu c tr c hoành và bán kínhỉ ộ ụ
đ ng tròn n i ti ptam giác ABC b ng 2 . Tìm t a đ tr ng tâm G c a tam giác ABC .ườ ộ ế ằ ọ ộ ọ ủ
2).Cho đ ng th ng (d) : ườ ẳ
x t
y 1
z t
=
= −
= −
và 2 mp (P) : x + 2y + 2z + 3 = 0 và (Q) : x + 2y + 2z + 7 = 0
a. Vi t ph ng trình hình chi u c a (d) trên (P) ế ươ ế ủ
b. L p ph.trình m t c u có tâm I thu c đ ng th ng (d) và ti p xúc v i hai m t ph ng (P) vàậ ặ ầ ộ ườ ẳ ế ớ ặ ẳ
(Q)
3). Ch n ng u nhiên 5 con bài trong b tú l kh . Tính xác su t sao cho trong 5 quân bài đó cóọ ẫ ộ ơ ơ ấ
đúng 3quân bài thu c 1 b ( ví d 3 con K )ộ ộ ụ
----------------------------- H t -----------------------------ế
Cán b coi thi không gi i thích gì thêm.ộ ả
trêng thpt hËu léc 2
®¸p ¸n ®Ò thi thö ®¹i häc lÇn 1 n¨m häc 2009-2010
M«n thi: to¸n
Thêi gian lµm bµi: 180 phót, kh«ng kÓ thêi gian giao ®Ò
C©u Néi dung §iÓm
I
2.0®
1
1,25
®
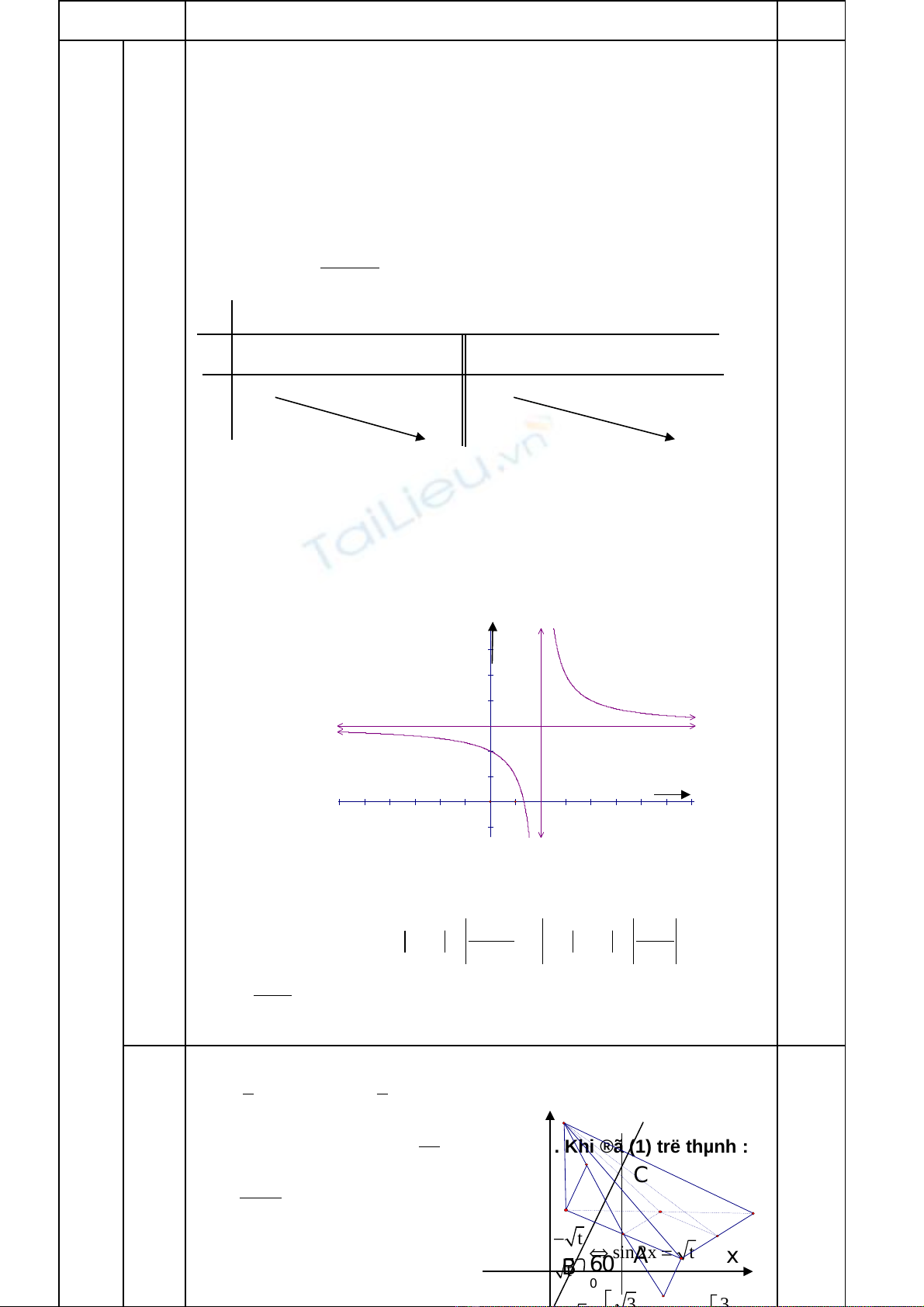
•Kh¶o s¸t vµ vÏ §THS
- TX§: D =
R
\ {2}
- Sù biÕn thiªn:
+ ) Giíi h¹n :
x x
Lim y Lim y 3
→−∞ →+∞
= =
nªn ®êng th¼ng y = 3 lµ tiªm cËn
ngang cña ®å thÞ hµm sè
+)
x 2 x 2
Lim y ; Lim y
− +
→ →
= −∞ = +∞
. Do ®ã ®êng th¼ng x = 2 lµ tiÖm cËn
®øng cña ®å thÞ hµm sè
+) B¶ng biÕn thiªn:
Ta cã : y’ =
( )
2
2
2x
−−
< 0 ,
x D∀ ∈
Hµm sè nghÞch biÕn trªn mçi kho¶ng
( )
−∞;2
vµ
- §å thÞ
+ Giao ®iÓm víi trôc tung : (0 ;2)
+ Giao ®iÓm víi trôc hoµnh : ( 4/3 ; 0)
+ §THS nhËn giao ®iÓm I(2 ;3) cña hai ®êng tiÖm cËn lµm t©m
®èi xøng
•Gäi M(x;y)
∈
(C) vµ c¸ch ®Òu 2 tiÖm cËn x = 2 vµ y = 3
| x – 2 | = | y – 3 |
3x 4 x
x 2 2 x 2
x 2 x 2
−
⇔ − = − ⇔ − =
− −
( )
x 1
xx 2 x 4
x 2
=
⇔ = ± − ⇔ =
−
VËy cã 2 ®iÓm tho¶ m·n ®Ò bµi lµ : M1( 1; 1) vµ M2(4; 6)
0,25
0,25
0,25
0.5
2
0.75
®
XÐt ph¬ng tr×nh : sin6x + cos6x = m ( sin4x + cos4x ) (2)
2 2
3 1
1 sin 2x m 1 sin 2x
4 2
⇔ − = −
÷
(1)
§Æt t = sin22x . Víi
2
x 0; 3
π
∈
th×
[ ]
t 0;1∈
. Khi ®ã (1) trë thµnh :
2m =
3t 4
t 2
−
−
víi
[ ]
t 0;1∈
NhËn xÐt : víi mçi
[ ]
t 0;1∈
ta cã :
sin 2x t sin 2x t
sin 2x t
= − ⇔ =
=
§Ó (2) cã 2 nghiÖm thuéc ®o¹n
2
0; 3
π
th×
) )
3 3
t ;1 t ;1
2 4
∈ ⇒ ∈
0,25
y’
y
x
+∞
−∞
-
+∞
−∞
-
2
3
3
O
y
xA
B
C
60
0
6
4
2
-5
5
x
O
y
N
M
D
S
A
B
C
K