
Một số quy tắc vẽ trong Hình học
Fractal
Chúng ta đã tìm hiểu vẻ đẹp của hình học Fractal,
các Fractal tự nhiên ở bài viết trước. Bài viết này tiếp tục cung cấp
cho các bạn một số quy tắc đơn giản để xây dựng một Fractal, chúng ta
chỉ xem hình minh hoạ để dễ hình dung (không biểu diễn dưới dạng công
thức). Chúng ta cũng có thể tạo cho mình những Fractal theo quy luật
riêng của chính chúng ta…
Tam giác Sierpinski
Sierpinski Triangle
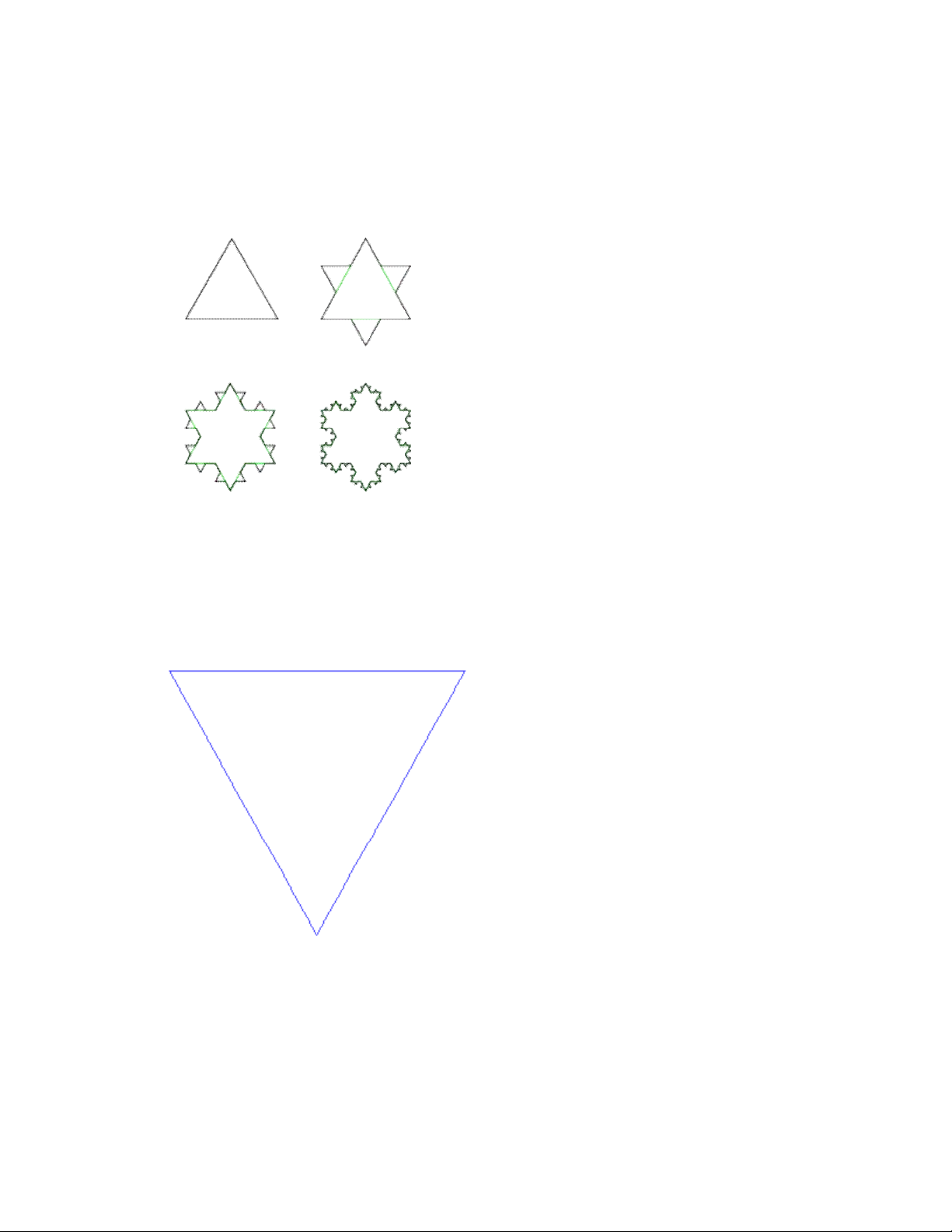
Bông tuyết Koch
Koch snowflake
Koch snowflake
Đường cong Koch (Koch curve)
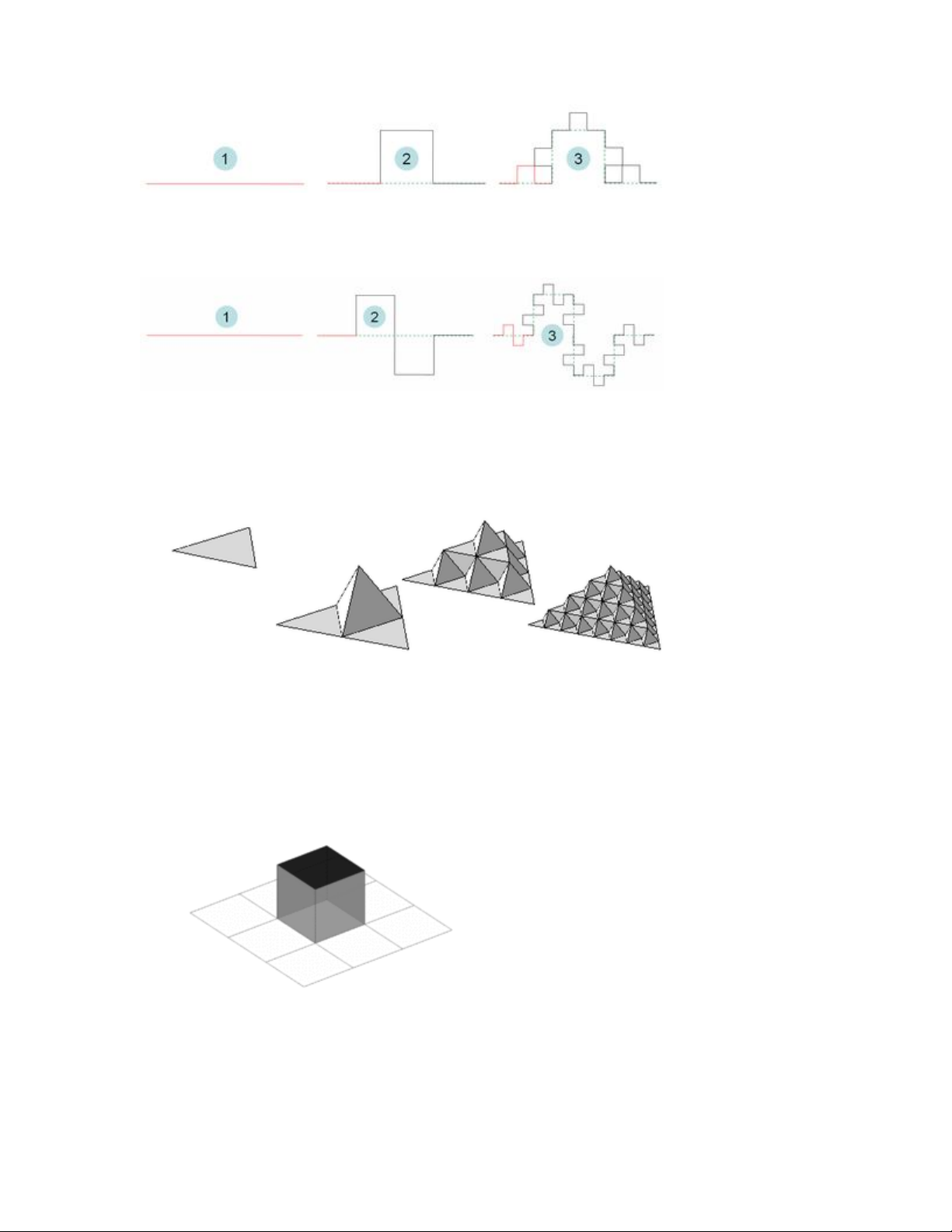
Đường cong
Koch 1 chiều
Đường cong
Koch 1 chiều
Đường cong
Koch 2 chiều
Đường cong Koch 2 chiều
Khối lập phương Menger/ Sierpinski (The Menger Sponge)

The Menger Sponge
Vẽ núi bằng Fractal
Vẽ
núi bằng Fractal
Một số Fractal nghệ thuật

















![Đề cương bài giảng Mỹ thuật đại cương [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250715/kimphuong1001/135x160/30821752564027.jpg)









