Phân hoá của vành đa thức theo các phần tử liên hợp và ứng dụng trong lý thuyết mã

Chia sẻ: Quanghai Quanghai | Ngày: | Loại File: DOC | Số trang:13

Thêm vào BST

Báo xấu

260
lượt xem 30
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

M• xyclic cục bộ (XCB) tuy còn non trẻ nhưng đ• tỏ ra có nhiều ưu điểm thoả m•n được yêu cầu thực tế của hệ thống truyền tin. Trong bài báo này, chúng tôi sẽ đề cập đến một cách phân hoạch mới trên vành đa thức chẵn Z2[x]/x2n+1 (ký hiệu là Z2n) đó là phân hoạch theo lớp các phần tử liên hợp và từ đây xây dựng m• XCB cụ thể trên phân hoạch này.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Phân hoá của vành đa thức theo các phần tử liên hợp và ứng dụng trong lý thuyết mã

LÜnh vùc C«ng nghÖ th«ng tin Ph©n ho¹ch cña vµnh ®a thøc theo c¸c phÇn tö liªn hîp vµ øng dông trong lý thuyÕt m· PGS.TS NguyÔn B×nh, KS. §Æng Hoµi B¾c Khoa Kü thuËt ®iÖn tö 1 Tãm t¾t: M· xyclic côc bé (XCB) tuy cßn non trÎ nhng ®· tá ra cã nhiÒu u ®iÓm tho¶ m·n ®îc yªu cÇu thùc tÕ cña hÖ thèng truyÒn tin. Trong bµi b¸o nµy, chóng t«i sÏ ®Ò cËp ®Õn mét c¸ch ph©n ho¹ch míi trªn vµnh ®a thøc ch½n Z 2[x]/x 2n+1 (ký hiÖu lµ Z 2n) ®ã lµ ph©n ho¹ch theo líp c¸c phÇn tö liªn hîp vµ tõ ®©y x©y dùng m· XCB cô thÓ trªn ph©n ho¹ch nµy. 1. Ph©n ho¹ch cña vµnh ®a thøc Z 2n theo c¸c phÇn tö liªn hîp 1.1 C¸c thÆng d bËc 2 vµ c¸c c¨n bËc 2 cña chóng. §Þnh nghÜa 1.1: §a thøc f(x) ®îc gäi lµ thÆng d bËc 2 (quadratic residue - QR) trong Z 2n nÕu tån t¹i ®a thøc g(x) sau: g2(x) ≡ f(x) mod x2n+1 (1.1) Nh vËy g(x) ∈ Z2n vµ ®îc gäi lµ c¨n bËc 2 (Square root - Sqr) cña f(x). NÕu g(x) = f ( x ) ®îc gäi lµ c¨n bËc 2 chÝnh cña f(x). Ch¼ng h¹n nÕu: f(x)= 1+ x 2 + x 4 th× c¨n bËc 2 chÝnh cña nã lµ: f ( x ) = 1+ x + x 2 Bæ ®Ò 1.1:§a thøc f(x) n»m trong tËp c¸c thÆng d bËc 2 Q2n ( f(x) ∈ Q2n ) khi vµ chØ khi f(x) chøa c¸c ®¬n thøc cã sè mò ch½n. Sè c¸c thÆng d bËc 2 trong Z2n ®îc x¸c ®Þnh nh sau: n  2n Q = ∑C i=0 i n 3 ( n −1) = Cn + Cn + Cn + ... + Cn + Cn = 2n 1 2 n (1.2) VÝ dô 1.1: Ta xÐt vµnh Z2n víi n=3 ta cã vµnh Z6 ( n = 3) TËp c¸c thÆng d bËc hai Q2n trong vµnh Z6 ®îc x¸c ®Þnh theo bæ ®Ò 2.1 nh sau: Q6 ={0, 1, x 2, x 4, 1+x 2, 1+x 4, x 2+x 4, 1+x 2+x 4} ( cã tÊt c¶ 23 - tøc 2n - phÇn tö) Häc viÖn C«ng nghÖ BCVT
Héi nghÞ Khoa häc lÇn thø 5 Bæ ®Ò 1.2: C¸c c¨n bËc 2 cña mét thÆng d bËc 2 ®îc x¸c ®Þnh theo c«ng thøc sau:   sqr[f(x)] = g(x) = (1+xn )  ∑ x  + f ( x ) t  t∈U  (1.3) Trong ®ã U lµ mét tËp gåm c¸c tæ hîp tuú ý c¸c gi¸ trÞ trong tËp s = {0, 1, 2,..., n- 1} Do vËy lùc lîng cña U sÏ b»ng: = 2n -1 U VÝ dô 1.2: Trong tËp Q6 ë trªn ta xÐt mét QR bÊt kú ®Ó x¸c ®Þnh c¨n bËc 2, ch¼ng h¹n f(x)=x 2 ¸p dông c«ng thøc (1.3) tÝnh c¸c c¨n bËc hai ë trªn ta cã  t  sqr(x 2) = (1+x 3)  ∑ x  + x (víi f ( x ) =x)  t∈U  + khi U= {0, 1, 2} sqr(x 2) = (1+x 3)( 1+x+x 2) + x = 1+x 2+x 3+x 4+x 5 + T¬ng tù ta cã: khi U = {0,1} sqr(x2) = (1+x3)( 1+x) + x = 1+x3+x4 Cø nh vËy ta sÏ t×m ®îc toµn bé 22n phÇn tö liªn hîp cña vµnh Z6. NhËn xÐt: - Trong vµnh Z2n cã 2n thÆng d bËc 2, mçi thÆng d bËc 2 cã 2n c¨n bËc 2, vËy cã tÊt c¶ 22n c¨n bËc 2 trong vµnh, c¸c c¨n bËc 2 nµy t¹o nªn toµn bé vµnh Z2n. - Ta sÏ gäi c¸c c¨n bËc 2 cña cïng mét thÆng d bËc 2 lµ c¸c phÇn tö liªn hîp (Conjugate Elements ) t ¬ng øng víi thÆng d ®ã ký hiÖu lµ CEs. 1.2 Ph©n ho¹ch vµnh Z 2[x]/ x2n+1 theo c¸c phÇn tö liªn hîp §Ó kh¶o s¸t sù ph©n ho¹ch theo c¸c CE trªn vµnh Z 2[x]/x 2n+1, ta sÏ kh¶o s¸t trªn vµnh cô thÓ Z6(n=3). TËp c¸c QR trong vµnh Z6 lµ: Q6 ={0, 1, x 2, x 4, 1+x 2, 1+x 4, x 2+x 4, 1+x 2+x 4} Vµnh Z 6 Sqr (x 2) Sqr (x 4) Sqr (0) Sqr (1) Sqr (1+x 2+x 4) Sqr (1+x 4) Sqr (x 2+x 4) Sqr (1+x 2) Häc viÖn C«ng nghÖ BCVT
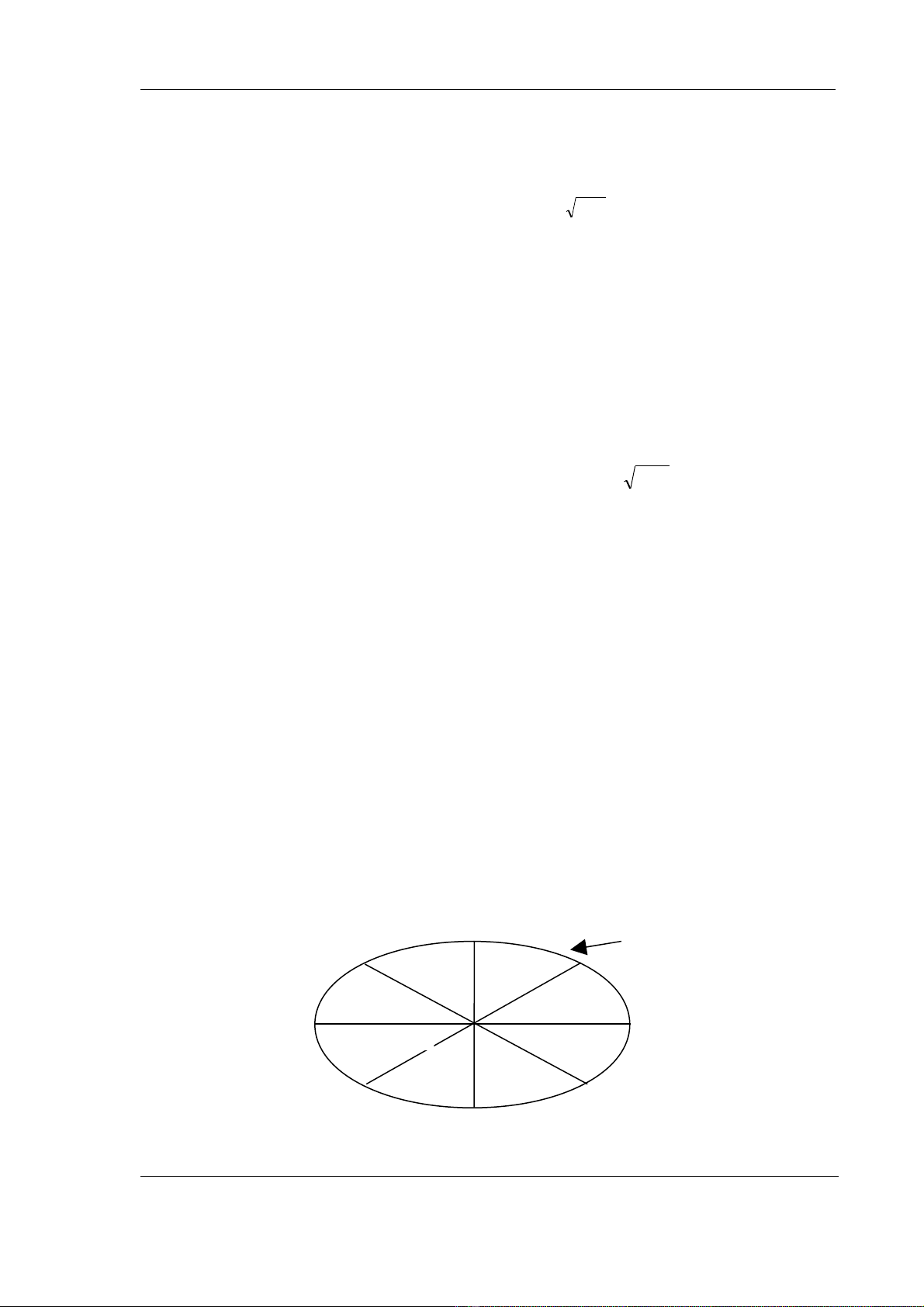
LÜnh vùc C«ng nghÖ th«ng tin H×nh 1. Ph©n ho¹ch vµnh Z 6 theo líp c¸c phÇn tö liªn hîp Ta thÊy r»ng, ®èi víi phÐp céng ⊕ c¸c CEs ë h×nh 1 sÏ tho¶ m·n b¶ng 1 nh sau: ⊕ Sqr(1) Sqr(x 2) Sqr(x 4) Sqr(1+x 2) Sqr(1+x 4) Sqr(x 2+x 4) Sqr(1+x 2+x Sqr(0) 4 ) Sqr(1) Sqr(0) Sqr(1+x 2) Sqr(1+x 4) Sqr(x 2) Sqr(x 4) Sqr(1+x 2+x Sqr(x 2+x 4) Sqr(1) 4 ) Sqr(x 2) Sqr(1+x 2) Sqr(0) Sqr(x 2+x 4) Sqr(1) Sqr(1+x 2+x Sqr(x 4) Sqr(1+x 4) Sqr(x 2) 4 ) Sqrh(x 4) Sqr(1+x 4) Sqr(x 2+x 4) Sqr(0) Sqr(1+x 2+x Sqr(1) Sqr(x 2) Sqr(1+x 2) Sqr(x 4) 4 ) Sqr(1+x 2) Sqr(x 2) Sqr(1) Sqr(1+x 2+x Sqr(0) Sqr(x 2+x 4) Sqr(1+x 4) Sqr(x 4) Sqr(1+x 2) 4 ) Sqr(1+x 4) Sqr(x 4) Sqr(1+x 2+x Sqr(1) Sqr(x 2+x 4) Sqr(0) Sqr(1+x 2) Sqr(x 2) Sqr(1+x 4) 4 ) Sqr(x 2+x 4) Sqr(1+x 2+x Sqr(x 4) Sqr(x 2) Sqr(1+x 4) Sqr(1+x 2) Sqr(0) Sqr(1) Sqr(x 2+x 4) 4 ) Sqr(1+x 2+x Sqr(x 2+x 4) Sqr(1+x 4) Sqr(1+x 2) Sqr(x 4) Sqr(x 2) Sqr(1) Sqr(0) Sqr(1+x 2+x 4 ) 4 ) Sqr(0) Sqr(1) Sqr(x 2) Sqr(x 4) Sqr(1+x 2) Sqr(1+x 4) Sqr(x 2+x 4) Sqr(1+x 2+x 4 Sqr(0) ) B¶ng 1. PhÐp céng modulo víi c¸c phÇn tö liªn hîp trong vµnh Z 6 Ta kiÓm tra mét phÐp céng modulo trong b¶ng trªn ch¼ng h¹n: Sqr(1)+Sqr(x 4) = Sqr(1+x 4) Ta cã: 1+x+x 4∈sqr(1) x 5∈ Sqr(x 4) 1+x+x 4 ⊕ x 5 = 1+x+x 4+x 5 ∈ Sqr(1+x 4) ( tho¶ m·n) KiÓm tra víi c¸c tæng kh¸c trong b¶ng 1, chóng ta thÊy chóng ®Òu tháa m·n do vËy râ rµng lµ líp c¸c phÇn tö liªn hîp t¹o nªn mét nhãm Aben céng tÝnh. + §èi víi phÐp nh©n, líp c¸c phÇn tö liªn hîp trong vµnh Z6 còng tho¶ m·n b¶ng sau: ⊗ Sqr(1) Sqr(x 2) Sqr(x 4) Sqr(1+x Sqr(1+x Sqr(x 2+x Sqr(1+x 2+x Sqr(0 2 ) 4 ) 4 ) 4 ) ) Sqr(1) Sqr(1) Sqr(x 2) Sqr(x 4) Sqr(1+x 2 Sqr(1+x 4 Sqr(x 2+x 4 Sqr(1+x 2+x 4 Sqr(0 ) ) ) ) ) Sqr(x 2) Sqr(x 2) Sqr(x 4) Sqr(1) Sqr(x 2+x Sqr(1+x 2 Sqr(1+x 4) Sqr(1+x 2+x 4 Sqr(0 4 ) ) ) ) Sqrh(x 4) Sqr(x 4) Sqr(0) Sqr(x 2) Sqr(1+x 4 Sqr(x 2+x Sqr(1+x 2) Sqr(1+x 2+x 4 Sqr(0 ) 4 ) ) ) Sqr(1+x 2) Sqr(1+x 2) Sqr(x 2+x 4) Sqr(1+x 4) Sqr(1+x 4 Sqr(x 2+x Sqr(1+x 2) Sqr(0) Sqr(0 ) 4 ) ) Sqr(1+x 4) Sqr(1+x 4) Sqr(1+x 2) Sqr(x 2+x 4) Sqr(x 2+x Sqr(1+x 2 Sqr(1+x 4) Sqr(0) Sqr(0 4 ) ) ) Häc viÖn C«ng nghÖ BCVT
Héi nghÞ Khoa häc lÇn thø 5 Sqr(x 2+x 4) Sqr(x 2+x 4) Sqr(x 2+x 4) Sqr(1+x 2) Sqr(1+x 2 Sqr(1+x 4 Sqr(x 2+x 4 Sqr(0) Sqr(0 ) ) ) ) Sqr(1+x 2+x Sqr(1+x 2+x Sqr(1+x 2+x Sqr(1+x 2+x Sqr(0) Sqr(0) Sqr(0) Sqr(1+x 2+x 4 Sqr(0 4 ) 4 ) 4 ) 4 ) ) ) Sqr(0) Sqr(0) Sqr(0) Sqr(0) Sqr(0) Sqr(0) Sqr(0) Sqr(0) 0 B¶ng 2. PhÐp nh©n modulo víi c¸c phÇn tö liªn hîp trong vµnh Z 6 Ta kiÓm tra c¸c kÕt qu¶ trong b¶ng trªn, ch¼ng h¹n nh: Sqr(1+x 2)x Sqr(x 4) = Sqr(1+x 4) (lu ý Sqr(1+x 4) = Sqr((1+x 2) x x 4)) XÐt: (x 3+x 4) ∈ Sqr(1+x 2) vµ (1+x 2+x 3) ∈ Sqr(1+x+x 2) Ta cã: (x 3+x 4)x(1+x 2+x 3) = (x 3+x 4+x 6+x 5+x 6+x 7)mod(x 6+1) = x+x 3+x 4+x 5 ∈ Sqr(1+x 4) Mét c¸ch t ¬ng tù nh trªn ta cã thÓ kiÓm tra toµn bé c¸c phÐp nh©n gi÷a c¸c cÆp c¸c phÇn tö liªn hîp nh trong b¶ng 2. Tõ kÕt qu¶ ë b¶ng 2 ta thÊy r»ng, c¸c phÇn tö liªn hîp trong vµnh Z 6 t¹o nªn mét nhãm theo phÐp nh©n víi phÇn tö ®¬n vÞ lµ Sqr(1), nhng lu ý sÏ cã tr - êng hîp hai phÇn tö kh¸c 0 nhng khi thùc hiÖn phÐp nh©n theo mod (x6+1), ta l¹i nhËn ®îc kÕt qu¶ l¹i b»ng 0. Ta cã thÓ lÊy vÝ dô : (x+x 3) ∈ Sqr(1+x 2) (1+x 2+x 4) ∈ Sqr(1+x 2+x 4) Khi thùc hiÖn phÐp nh©n: (x+x 3) x (1+x 2+x 4) = (x+x 3+x 3+x 5+x 5+x 7) mod (x6+1) = x+x = 0. VËy, c¸c phÇn tö liªn hîp cña c¸c thÆng d bËc 2 trong vµnh Z6 t¹o nªn mét nöa nhãm nh©n. NhËn xÐt: - Líp c¸c CE cña c¸c thÆng d bËc 2 trong vµnh Z6 lµ mét nhãm ®Çy ®ñ ®èi víi phÐp céng vµ nöa nhãm ®èi víi phÐp nh©n. - Líp c¸c CE trong vµnh Z6 tho¶ m·n c¸c tiªn ®Ò vÒ vµnh, chóng t¹o nªn mét vµnh. §iÒu nµy còng ®óng cho c¸c phÇn tö liªn hîp cña mäi vµnh ®a thøc Z 2n víi c¸c n kh¸c nhau. 2. X©y dùng m· XCB theo c¸c ph©n tö liªn hîp cña luü ®¼ng nuèt 2.1 X©y dùng m· theo líp CEs cña luü ®¼ng nuèt trªn vµnh Z 10 theo ph©n ho¹ch chuÈn Häc viÖn C«ng nghÖ BCVT
LÜnh vùc C«ng nghÖ th«ng tin Theo kÕt qu¶ phÇn trªn ta thÊy líp c¸c phÇn tö liªn hîp trªn Z2n lu«n cã cÊu tróc cña mét vµnh ®¹i sè, dùa vµo cÊu tróc ®¹i sè nµy ta hoµn toµn cã thÓ x©y dùng ®îc m· XCB. n −1 Trong vµnh Z 2 [ x ] x + 1 lu«n tån t¹i e 0 ( x ) = ∑ x ®îc gäi lµ luü ®¼ng n i i =0 nuèt. T¬ng tù nh vËy, trong vµnh Z2n, ta còng x¸c ®Þnh ®îc mét lòy ®¼ng nuèt lµ e 0 ( x 2 ) víi : n −1 e0 (x 2 ) = ∑ x 2i (2.1) i=0 PhÐp nh©n mét ®a thøc bÊt kú víi luü ®¼ng nuèt gióp ta kiÓm tra ®îc tÝnh ch½n lÎ. Luü ®¼ng nuèt cã nh÷ng tÝnh chÊt ®Æc biÖt ®Ó x©y dùng m· XCB. Trong vµnh Z 2 [ x ] x10 + 1 , tøc vµnh Z2n víi n = 5 ta thÊy r»ng cã tÊt c¶ 32 (2n) thÆng d bËc 2 mçi thÆng d bËc 2 cã tÊt c¶ 32 (2n) phÇn tö liªn hîp. C¸c thÆng d bËc 2 trong vµnh lµ c¸c ®a thøc bao gåm c¸c ®¬n thøc cã sè mò ch½n ®- îc x¸c ®Þnh nhê bæ ®Ò 1.1. Q10 = {0, 1, x2, x4, x6, x8, 1+x2, 1+x4, 1+x6, 1+x8, x2+x4, x2+x6, x2+x8, x4+x6, x4+x8, x6+x8, 1+x2+x 4, 1+x2+x6, 1+x2+x 8, 1+x4+x 6, 1+x4+x 8, 1+x6+x 8, x 2+x 4+x 6, x 2+x 4+x 8, x 2+x 6+x 8, x 4+x 6+x8, 1+x2+x 4+x 6, 1+x2+x4+x8, 1+x2+x 6+x 8, 1+x4+x 6+x 8, x 2+x 4+x 6+x 8, 1+x2+x 4+x 6+x 8} C¸c phÇn tö liªn hîp cña luü ®¼ng nuèt e0(x 2)=1+x 2+x 4+x 6+x 8 Ta x¸c ®Þnh CEs cña luü ®¼ng nuèt e0(x 2)=1+x 2+x 4+x 6+x 8 trong tËp Q10 trªn theo biÓu thøc:   Sqr(e0(x 2)) = (1+x n)  ∑ x  + t e0 ( x 2 )  t∈U  (2.2) Toµn bé c¸c phÇn tö liªn hîp cña luü ®¼ng nuèt ®îc thÓ hiÖn ë b¶ng bªn tr¸i, b¶ng bªn ph¶i thÓ hiÖn ph©n ho¹ch cña c¸c luü ®¼ng nuèt trong vµnh Z10 theo ph©n ho¹ch chuÈn (ph©n ho¹ch trong ®ã c¸c phÇn tö trong mét líp dÞch vßng theo c¸c tr ëng líp kÒ) . Häc viÖn C«ng nghÖ BCVT
Héi nghÞ Khoa häc lÇn thø 5 qr(e0(x2)) = N C1 C2 C3 C3 {1+x+x 2+x3+x4,+x2+x 3+x 4+x6,1+x 2+x 4+x 6+x 8, 0 1+x3+x4+x6+x7, x+x 2+x3+x4+x5, x+x 3+x 4+x 5+x 7, 1 (01234 (02346 (03467 (02468 x+x 3+x5+x 7+x9, x+x 4+x 5+x 7+x 8, x 2+x 3+x 4+x 5+x 6, ) ) ) ) x 2+x4+x5+x6+x8, x2+x5+x 6+x 8+x 9, 2 (12345 (13457 (14578 (13579 x 3+x4+x5+x6+x7, x3+x5+x6+x7+x9, 1+x3+x 6+x 7+x 9, ) ) ) ) 3 (23456 (24568 (25689 x 4+x5+x6+x7+x8, 1+x4+x6+x7+x8, 1+x+x 4+x 7+x 8, ) ) ) x 5+x6+x7+x8+x9, x+x 5+x7+x8+x9, x+x 2+x 5+x 8+x 9, Ph© 4 (34567 (35679 (36790 1+x6+x7+x8+x9, 1+x2+x6+x8+x9, 1+x2+x 3+x 6+x 9, n ) ) ) 1+x2+x7+x8+x9, 1+x+x 3+x7+x9, 1+x+x 3+x 4+x 7, ho¹c 5 (45678 (46780 (47801 1+x+x 2+x 8+x 9, 1+x+x 2+x 4+x 8, x+x 2+x 4+x 5+x 8, h ) ) ) 1+x+x 2+x 3+x 9, x+x 2+x3+x5+x 9, x 2+x 3+x 5+x 6+x 9 } 6 (56789 (57891 (58912 ) ) ) 7 (67890 (68902 (69023 ) ) ) 8 (78901 (79013 (70134 ) ) ) 9 (89012 (80124 (81245 ) ) ) 1 (90123 (91235 (92356 0 ) ) ) B¶ng 3. Ph©n ho¹ch chuÈn cña c¸c CE trªn vµnh Z 10 Bæ ®Ò 2.1:TËp tÊt c¶ c¸c phÇn tö liªn hîp víi luü ®¼ng nuèt e0(x2) sÏ t¹o ra c¸c m· xyclic côc bé víi c¸c gi¸ trÞ sau: (n, k, d 0) = ( 2n - 1, n, 2n-1) §©y lµ m· tèi u tho¶ m·n giíi h¹n Griesmer nghÜa lµ ®é dµi tõ m· n tho¶ m·n: k −1 d  n ≥ ∑ 0  i (2.2) i =0  2  NhËn xÐt: - §Ó trùc giao hãa hÖ tæng kiÓm tra a ( x ) + b( x ) = 1 + x n , ta cã thÓ chän tr íc gi¸ trÞ cña n dÊu th«ng tin. §Ó thuËn tiÖn, b¾t ®Çu tõ ®©y khi lËp m· ta sÏ chän x n = x n +1 =  = x 2n −1 = 0 ). 4 x 0x 1x 2x 3x 00000 - Tõ toµn bé c¸c líp kÒ, ta cã thÓ x©y dùng m· (31, 5) víi d 0 = 16 . Sau ®©y, ta sÏ x©y dùng m· xyclic côc bé cô thÓ tõ c¸c líp kÒ C 1, C2 vµ C3 trong b¶ng 3.1. C¸c phÇn tö (5 6 7 8 9) kh«ng cÇn ph¸t v× theo gi¶ ®Þnh chóng + + + + Häc viÖn C«ng nghÖ BCVT + + + +
LÜnh vùc C«ng nghÖ th«ng tin ®Òu b»ng 0, nhng ®Ó nhËn biÕt chóng khi gi¶i m· ph¶i thªm 0 vµo, do ®ã m· xyclic côc bé nµy cã chiÒu dµi lµ 29. M· nµy chÝnh lµ m· (29, 5) víi d0 = 14 ®©y m· gÇn tèi u (29, 5, 14) víi s¬ ®å lËp m· nh sau: H×nh 2. S¬ ®å m· ho¸ m· (29,5) theo c¸c líp kÒ C1, C2, C3 Ta cã thÓ ph¸t bÊt kú tõ m· C1 hoÆc C2 hoÆc C3 tuú theo chän bit. Sau 5 nhÞp dÞch vßng x¸c ®Þnh ®îc 5 dÊu th«ng tin tõ x 0 ®Õn x 4. Sau ®©y lµ s¬ ®å gi¶i m·. C1 C3 C3 C3 C5 C3 C3 C8 C3 C10 C1 C2 C3 C2 C5 C6 C7 C8 C9 C10 3 2 3 4 3 6 7 3 9 3 2 2 2 4 2 2 2 2 2 2 C1 C1 C1 C1 C1 C1 C1 C1 C1 C10 1 2 3 4 5 6 7 8 9 1 + + + + + + + + + + + + + Häc viÖn C«ng nghÖ BCVT + M=8 H×nh 3. Bé gi ¶i m· m· XCB (29,5) theo ph©n ho¹ch OUTPUT
Héi nghÞ Khoa häc lÇn thø 5 Bé gi¶i m· ngìng cña m· nµy ®îc thÓ hiÖn ë h×nh 3. T¹i xung clock thø nhÊt, ®Çu ra cña thiÕt bÞ gi¶i m· M lµ x 0. T¹i xung clock thø hai, ®Çu ra cña M lµ x. T¹i xung clock thø ba, ®Çu ra cu¶ M lµ x 2. T¹i xung clock thø t , ®Çu ra lµ x 3. T¹i xung clock thø 5, ®Çu ra lµ x 4. Ngìng chÝnh cña thiÕt bÞ gi¶i m· ngìng M sÏ lµ 8. Bé m· cã kh¶ n¨ng söa ®îc 6 bit sai. L u ®å thuËt to¸n m« pháng c¸ch lËp, gi¶i m· trªn ®îc thÓ hiÖn ë trang tiÕp theo. 2.2 X©y dùng m· theo líp CEs cña luü ®¼ng nuèt trªn vµnh Z 10 theo ph©n ho¹ch cùc ®¹i Trong vµnh Z 2 [ x ] x10 + 1 , nhãm nh©n víi phÇn tö sinh lµ phÇn tö nguyªn thuû a(x) = 1+x+x 2 ®îc x¸c ®Þnh nh sau: a ( x ) = 1 + x + x 2 ⇔ (012) A= {ai (x), 1, 30 } = {(012), (024)), (01356), (048), (1245689), (6), (678), (068), (12679), (046), (0124578), (2), (234), (246), (23578), (026), (0134678), (8), (089), (028), (13489), (268), (0234679), (4), (456), (468), (04579), (248), (0235689),(0)} Sau ®©y chóng ta sÏ xem xÐt c¸ch x©y dùng m· xyclic côc bé cô thÓ trªn mét ph©n ho¹ch cùc ®¹i theo c¸c phÇn tö liªn hîp cña luü ®¼ng nuèt trªn vµnh Z10. Víi n = 5, 32 phÇn tö cña luü ®¼ng e 0 ( x 2 ) ®îc ph©n ho¹ch theo hai líp kÒ nh sau: B1 = {e 0 ( x )a i ( x ), i = 0, 29} = {b i , b = 1, 30} Häc viÖn C«ng nghÖ BCVT
LÜnh vùc C«ng nghÖ th«ng tin B 1 = {(01234), (02346), (01478), (34567), (35679), (01347), (06789), (02689), (03467), (01239), (12359), (03679), (23456), (24568), (02369), (56789), (15789), (23569), (01289), (01248), (25689), (12345), (13457), (12589), (45678), (04678), (12458), (01789), (01374), (14578)}. B 2 = {(02468), (13579)} Ta sÏ sö dông líp kÒ B 1 ®Ó t¹o m· xyclic côc bé (29, 5) phÇn tö (5 6 7 8 9) = 0 v× theo gi¶ thiÕt x 5=x 6=x 7=x 8=x 9=0 Lu ®å thuËt to¸n vµ kÕt qu¶ ch¬ng tr×nh m« pháng lËp m· , gi¶i m· m· (29, 5) theo ph©n ho¹ch chuÈn b»ng Visual C ++ L u ®å thuËt to¸n: Begin NhËp ®a thøc th«ng §a t høc t h«ng tin N cã hîp lÖ kh«ng? Y M · ho¸ vµ t r uyÒn (Send): - Chän tr -ëng líp kÒ cña C1, C2, C3 - DÞch vßng T¹o nhiÔu (Noise) N NhiÔu cã hîp lÖ kh«ng Y NhËn t h«ng t in (Receive) Receive = Send XOR Noise Gi¶i m·: J sè t æng k iÓm t r a ®· biÕt H iÓn thÞ tõ m· End Häc viÖn C«ng nghÖ BCVT
Héi nghÞ Khoa häc lÇn thø 5 KÕt qu¶ m« pháng: C¸ch m· hãa m· 29,5 theo ph©n ho¹ch cùc ®¹i: Gi¶ sö ta cã ®a thøc th«ng tin lµ I = {1 0 1 0 0} B»ng c¸ch thay lÇn l ît ®a thøc th«ng tin vµo c¸c ®a thøc trong nhãm nh©n xyclic ë trªn, vµ céng modul 2 kÕt qu¶ ta sÏ ®îc toµn bé tõ m· t ¬ng øng víi ®a thøc th«ng tin ®ã.VÝ dô, ®a thøc ®Çu tiªn cña nhãm nh©n lµ a = (1 + x + x 2 + x 3 + x 4 ), thay t ¬ng øng ®a thøc th«ng tin ë trªn vµo ta ®îc bit ®Çu tiªn cña tõ m· lµ: (1 + x 2) = 1 ⊕ 1 = 0. Thùc hiÖn víi tÊt c¶ c¸c bit cßn l¹i ta ®îc toµn bé tõ m· xyclic theo ph©n ho¹ch cùc ®¹i t ¬ng øng víi ®a thøc th«ng tin trªn lµ: 0010 0 1 1010 1 1 11 0 0 010 01101 011110 HÖ tæng kiÓm tra trùc giao víi 1 + x 5 ®îc x©y dùng tõ B1 lµ: S1 = b1 + b 22 S 2 = b 2 + b13 S3 = b 3 + b 30 S4 = b 4 + b9 S5 = b 5 + b12 S6 = b 6 + b 23 S7 = b 8 + b 21 S8 = b10 + b11 S9 = b15 + b18 S10 = b17 + b 28 S11 = b19 + b 24 S12 = b 20 + b 27 S13 = b 7 + b16 S14 = b 25 + b 26 Häc viÖn C«ng nghÖ BCVT
LÜnh vùc C«ng nghÖ th«ng tin §èi víi hÖ tæng kiÓm tra trùc giao nµy, ta cã thÓ chän x 5 = x 6 = x 7 = x 8 = x 9 = 0 . Trong tr êng hîp nµy, ta cã m· xyclic (29, 5) víi d 0 = 14 . Bé gi¶i m· ngìng cña m· nµy ®îc thÓ hiÖn trong h×nh 4. b30 b29 b28 b27 b26 b25 b24 b23 b22 b21 b20 b19 b18 b17 b16 b15 b14 b13 b12 b11 b10 b9 b8 b7 b6 b5 b4 b3 b2 b1 + + + + + + + M=8 + + + + + + + Häc viÖn C«ng nghÖ BCVT H×nh 4. Bé gi ¶i m· m· (29,5) theo ph©n ho¹ch cùc
Héi nghÞ Khoa häc lÇn thø 5 Gi¸ trÞ cña b16 b»ng zero, gi¸ trÞ nµy kh«ng ®îc truyÒn ®i, nhng nã ®îc thªm vµo trong qu¸ tr×nh gi¶i m·. T¹i xung nhÞp clock ®Çu tiªn, ®Çu ra cña thiÕt bÞ gi¶i m· ngìng M lµ x 0. T¹i xung clock thø 22, ®Çu ra cña M lµ x 1. T¹i xung clock thø 43, ®Çu ra cña M lµ x 2. T¹i xung clock thø 64, ®Çu ra cña M lµ x 3. T¹i xung clock thø 85, ®Çu ra cña M lµ x 4.§©y lµ xung nhÞp clock cuèi cïng cña qu¸ tr×nh gi¶i m·. Ngìng chÝnh cña M sÏ lµ 8. Bé m· söa ®îc 6 bit sai. Víi thuËt to¸n t ¬ng tù ta x©y dùng ch¬ng tr×nh m« pháng b»ng MATLAB vµ cã ®îc kÕt qu¶ nh sau: 3. KÕt luËn Ta thÊy r»ng viÖc x©y dùng c¸c m· theo c¸c phÇn tö liªn hîp cña luü ®¼ng nuèt cã nhiÒu u ®iÓm næi bËt nh: - C¸c m· t¹o ra ®Òu lµ m· gÇn tèi u tho¶ m·n c¸c giíi h¹n Griesmes. Häc viÖn C«ng nghÖ BCVT
LÜnh vùc C«ng nghÖ th«ng tin - Kh¶ n¨ng t¹o ra c¸c bé m· cã cïng tham sè lµ rÊt lín. §iÓn h×nh nh m· (29,5) chóng ta t¹o ra cã tíi h¬n 5400 kh¶ n¨ng. - C¸c s¬ ®å m· ho¸ vµ gi¶i m· ®Òu kh¸ ®¬n gi¶n chØ cÇn c¸c bé céng modulo 2 vµ nh©n ®a thøc th«ng th êng. - Dùa vµo ph¬ng ph¸p ph©n ho¹ch theo c¸c phÇn tö liªn hîp cña luü ®¼ng nuèt ta cã thÓ x©y dùng m· trªn mäi vµnh ch½n Z2n, ®iÒu mµ tr íc nay ch- a ®îc ®Ò cËp ®Õn. KÕt qu¶ cña bµi b¸o nÕu ®îc hoµn thiÖn vÒ phÇn cøng cã thÓ ®îc sö dông trong viÖc truyÒn tin trong c¸c m¹ng Lan, Wan... víi nh÷ng ®Æc tÝnh truyÒn dÉn vµ söa sai tèt, linh ho¹t trong viÖc thay ®æi bé m·. Tµi liÖu tham kh¶o [1] Nguyen Binh, Nguyen Xuan Quynh. "Application of symmetric characteristic of cosets for improving error - correcting ability of local cyclic codes". Science conference. Electronics - Informatics Institute. Hanoi, 1988. [2] Vò ViÖt: Ph©n ho¹ch vµnh ®a thøc. Chuyªn ®Ò tiÕn sÜ, 2001 [3] Nguyen Binh. Tran Duc Su, Pham Viet Trung. "Decomposition of polynomial ring according to the classes of conjugate elements". ATC - 26. Hanoi, 10.2001. [4] Nguyen Binh, Vu Viet, Pham Viet Trung. "Decomposition of polynomial ring and coding with random clock". CAFEO 2000. Hanoi, 22-24 Nov, 2000. Häc viÖn C«ng nghÖ BCVT

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn