Chương 2 : Cơ sở lý thuyết chung về phân tích động học vật rắn không gian
- 1 -
CHƯƠNG 2: CƠ SỞ LÝ THUYẾT CHUNG VỀ PHÂN TÍCH ĐỘNG
HỌC VẬT RẮN KHÔNG GIAN
2.1 Ma trận cosin chỉ hướng
2.1.1 Định nghĩa ma trận cosin chỉ hướng của vật rắn.
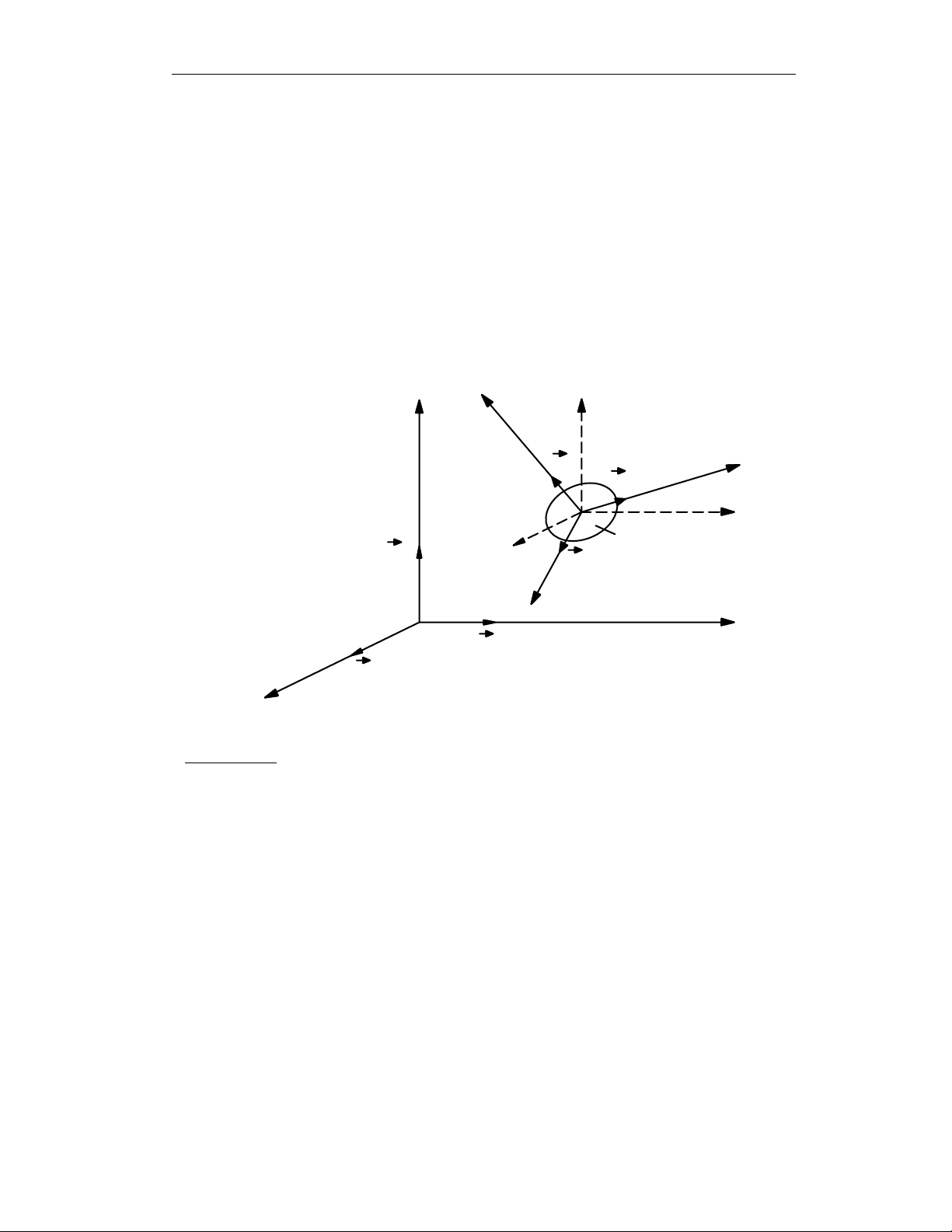
Cho vật rắn B và hệ qui chiếu R0=
{
}
(0) (0) (0)
123
,,eee
r
rr . Trong đó (0)
1
e
r, (0)
2
e
r, (0)
3
e
r
là ba vector đơn vị trên các trục Ox0,Oy0,Oz0. Ta gắn chặt vào vật rắn một hệ
qui chiếu R=
{
}
123
,,eee
rr r với 1
e
r
,2
e
r
,3
e
r
là ba vector đơn vị trên các trục
Ax,Ay,Az (Hình 2.1).
Hình 2.1
Định nghĩa : Ma trận vuông cấp ba
=A
(0) (0) (0)
11 12 13
(0) (0) (0)
21 22 23
(0) (0) (0)
31 32 33
...
...
...
eeee ee
eeee ee
eeee ee
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎣⎦
rrrr rr
rrrr rr
rrrr rr
(2.1)
được gọi là ma trận cosin chỉ hướng của vật rắn B đối với hệ qui chiếu R0.
Nếu ta đưa vào ký hiệu :
(0) (0)
.cos(,)
ij i i i i
aee ee==
rr r r
, (i,j = 1,2 3) (2.2)
Thì ma trận cosin chỉ hướng (2.1) có dạng:
=A
11 12 13
21 22 23
31 32 33
aaa
aaa
aaa
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎣⎦
(2.3)
O
e3
(0)
(0)
e1
e(0)
2
e3
e1
e2
X
Z
Y
X
B
A
0
0
Y
Z0Z1
Y1
X1
Chương 2 : Cơ sở lý thuyết chung về phân tích động học vật rắn không gian
- 2 -
Từ định nghĩa trên, trong hệ qui chiếu R0 ta có các hệ thức liên hệ:
(0) (0) (0)
1111 122 133
(0) (0) (0)
2211 222 233
(0) (0) (0)
3311 322 333
eaeaeae
eae ae ae
eae ae ae
=++
=++
=++
rrr
rrr
rrr
(2.4)
Nếu ta ký hiệu ei là ma trận cột gồm các phần tử của vector i
e
r trong hệ
qui chiếu R0
1=e
11
21
31
a
a
a
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎣⎦
, 2
=
e
12
22
32
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
, 3
=
e
13
23
33
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
(2.5)
Thì ma trận cosin chỉ hướng (2.3) có dạng:
A=[e1,e2,e3] (2.6)
Ma trận cosin chỉ hướng A còn được gọi là ma trận quay của vật rắn.
2.1.2 Một vài tính chất cơ bản của ma trận cosin chỉ hướng
a) Tính chất 1: Ma trận cosin chỉ hướng là ma trận trực giao.
Theo công thức (2.6) :
A=[e1,e2,e3]
Vậy ma trận cosin chỉ hướng A là ma trận cột có ba cột là ba vector trực
chuẩn. Do đó A là ma trận trực giao.
Hệ quả: Trong 9 thành phần của ma trận cosin chỉ hướng có 3 thành
phần độc lập.
Do tính chất của ma trận cosin chỉ hướng là ma trận trực giao nên
A.AT=E. Từ đó nhận được 6 phương trình liên hệ giữa các thành phần của
ma trận cosin chỉ phương như sau:
222
11 21 31
222
12 22 32
222
13 23 33
1
1
1
aaa
aaa
aaa
++=
++=
++=
,
11 12 21 22 31 32
11 13 21 23 31 33
12 13 22 23 32 33
0
0
0
aa aa aa
aa aa aa
aa aa aa
+
+=
+
+=
+
+=
Do vậy chỉ có ba thành phần của ma trận cosin chỉ hướng là độc lập.
b) Tính chất 2: Định thức của ma trận cosin chỉ hướng det(A)=1.
Từ hệ thức A.AT = E ta suy ra:
det(A.AT) = det(A).det(AT) = det(E) = 1
Do : det(A) = det(AT) nên to có det(A) = 1
±
. Ta có thể chứng minh
det(A) = 1.
Chương 2 : Cơ sở lý thuyết chung về phân tích động học vật rắn không gian
- 3 -
c) Tính chất 3 : Ma trận cosin chỉ hướng có ít nhất một trị riêng 11
λ
=.
2.1.3 Ý nghĩa của ma trận cosin chỉ hướng của vật rắn
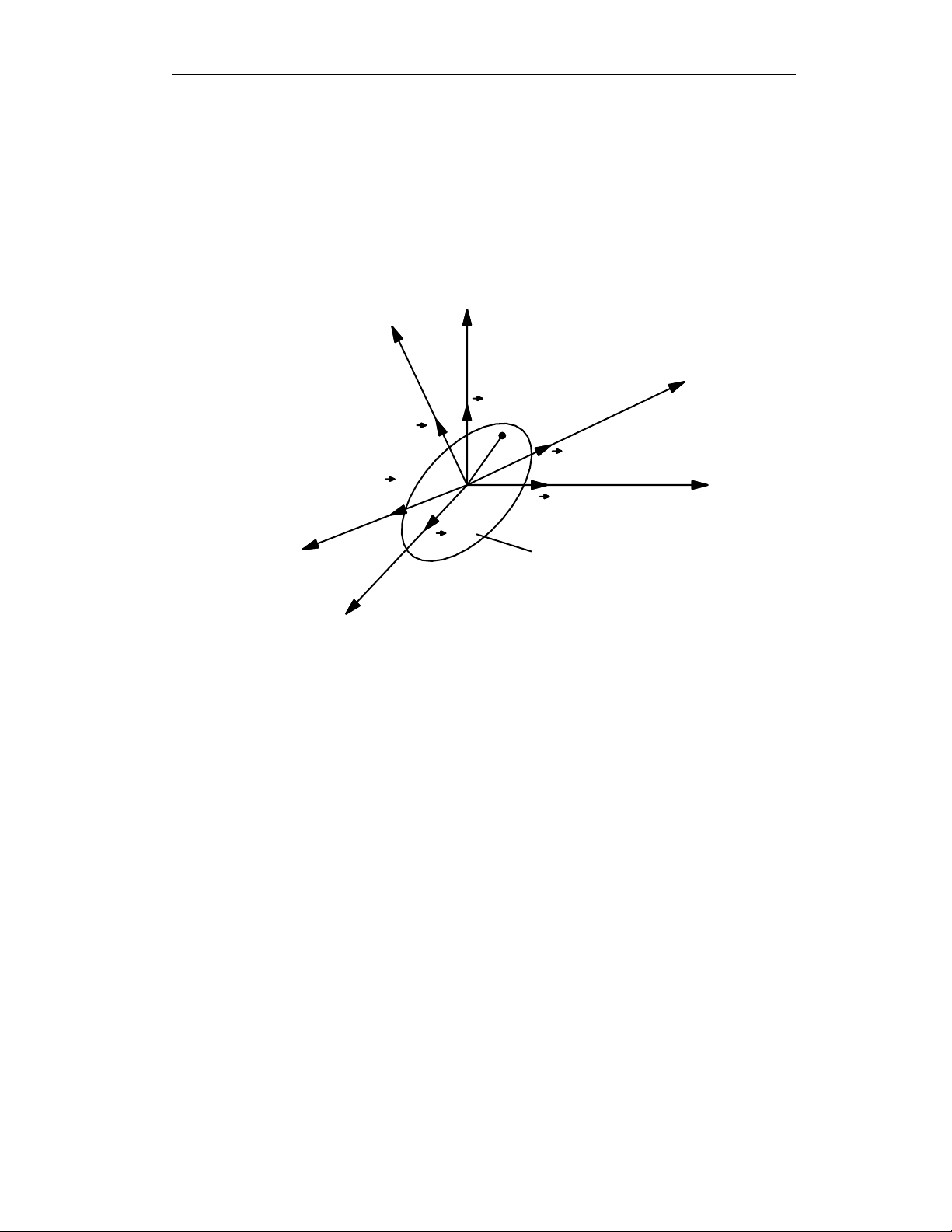
Xét hai hệ qui chiếu R0 và R có cùng gốc O. Trong đó hệ qui chiếu R0
≡
Ox0y0x0 là hệ qui chiếu cố định, hệ qui chiếu R
≡
Oxyz gắn liền với vật rắn
B. Lấy một điểm P bất kỳ thuộc vật rắn B. Vị trí của điểm P được xác định
bởi vector định vị
P
OP r=
uuurr. (Hình vẽ 2.2)
Hình 2.2
Ký hiệu các tọa độ của điểm P trong hệ qui chiếu động Oxyz là xP, yP, zP,
các tọa độ của điểm P trong hệ qui chiếu cố định Ox0y0z0 là (0)
P
x
, (0)
P
y, (0)
P
z .
Ta có các hệ thức sau :
(0) (0) (0) (0) (0) (0)
123
...
PP P P
rxe ye ze=++
rr r r
(2.7)
123
...
PP P P
rxeyeze=++
rr rr
(2.8)
Thế các biểu thức (2.4) vào hệ thức (2.8) ta được :
(0) (0) (0)
11 1 21 2 31 3
(. . . )
PP
rxae ae ae=+++
rrrr
(0) (0) (0)
12 1 22 2 32 3
(. . . )
P
yaeaeae
+
++
rrr
(2.10)
(0) (0) (0)
13 1 23 2 33 3
(. . . )
P
zaeaeae++
rrr
Hay :
(0)
11 12 33 1
(. . .)
PPPP
raxayaze=++ +
rr
(0)
31 32 33 2
(. . .)
PPP
ax ay aze++ +
r
(2.11)
(0)
31 32 33 3
(. . .)
PPP
ax ay aze++
r
e3
(0)
e2
(0)
e1
(0)
e3
e1
e2
Z
Y
Y
X
0
Z0
X0
P
B
Chương 2 : Cơ sở lý thuyết chung về phân tích động học vật rắn không gian
- 4 -
Z
Y
X
O
θ
Ψ
ϕ
So sánh các biểu thức (2.7) và (2.11) ta suy ra hệ phương trình :
(0)
11 12 33
...
P
PPP
x
ax ay az=++
(0)
31 32 33
...
P
PPP
yaxayaz=++ (2.12)
(0)
31 32 33
...
P
PPP
zaxayaz=++
Hệ phương trình (2.12) có thể viết lại dưới dạng ma trận như sau :
(0)
11 12 13
(0)
21 22 23
(0)
31 32 33
.
P
P
P
P
P
P
x
x
aaa
yaaay
aaa z
z
⎡⎤
⎡
⎤
⎡⎤
⎢⎥
⎢
⎥
⎢⎥
=
⎢⎥
⎢
⎥
⎢⎥
⎢⎥
⎢
⎥
⎢⎥
⎣⎦
⎣
⎦
⎣⎦
(2.13)
Từ hệ phương trình (2.13) ta rút ra kết luận sau : Ma trận cosin chỉ hướng
A biến đổi các tọa độ của điểm P bất kỳ thuộc vật rắn trong hệ qui chiếu
động Oxyz sang các tọa độ của điểm P đó trong hệ qui chiếu cố định Ox0-
y0z0.
2.2 Các ma trận quay cơ bản
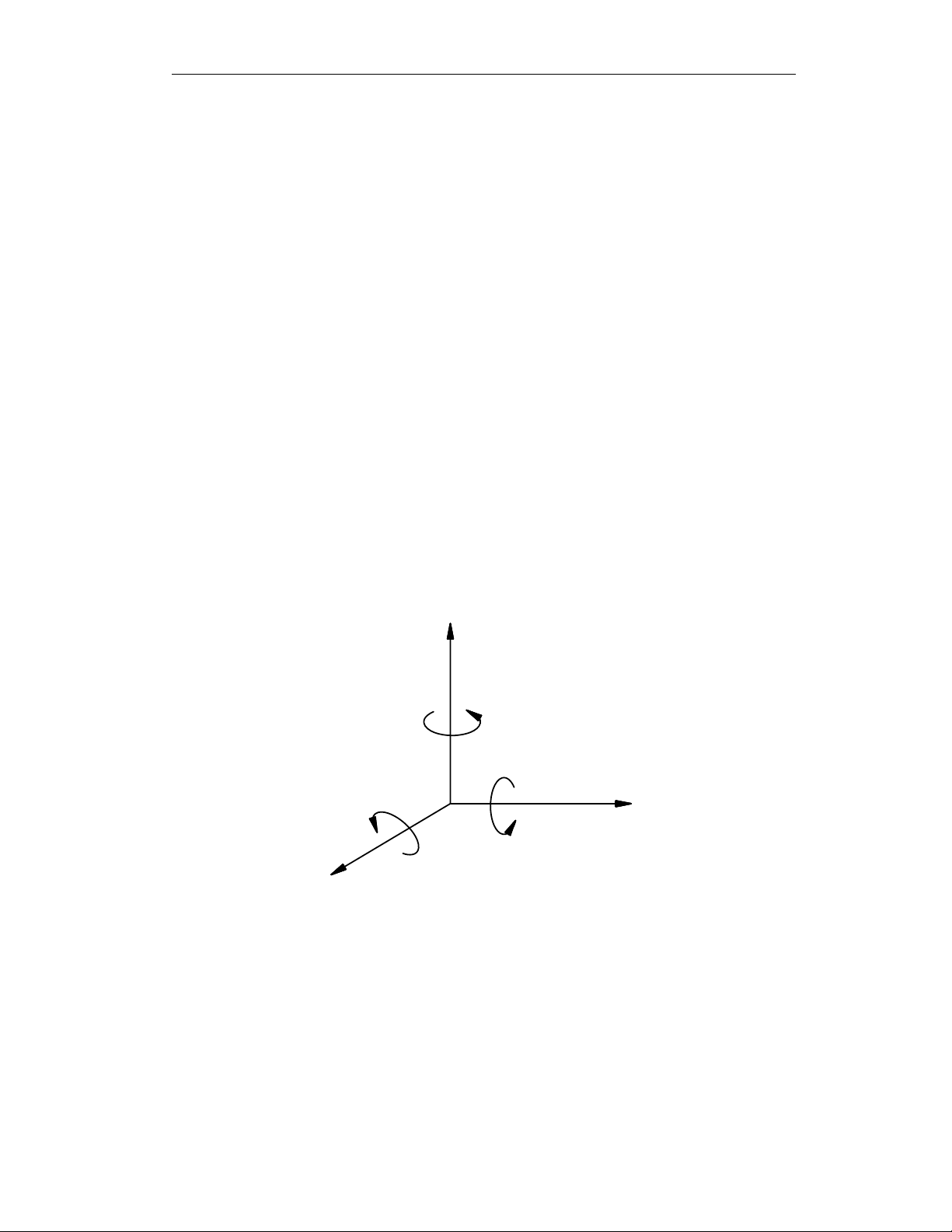
Ta qui ước hướng quay dương là hướng quay ngược chiều kim đồng hồ
như hình vẽ (Hình 2.3).
Hình 2.3
Các phép quay quanh trục x, y, z của hệ tọa độ vuông góc Oxyz được gọi là
phép quay cơ bản.
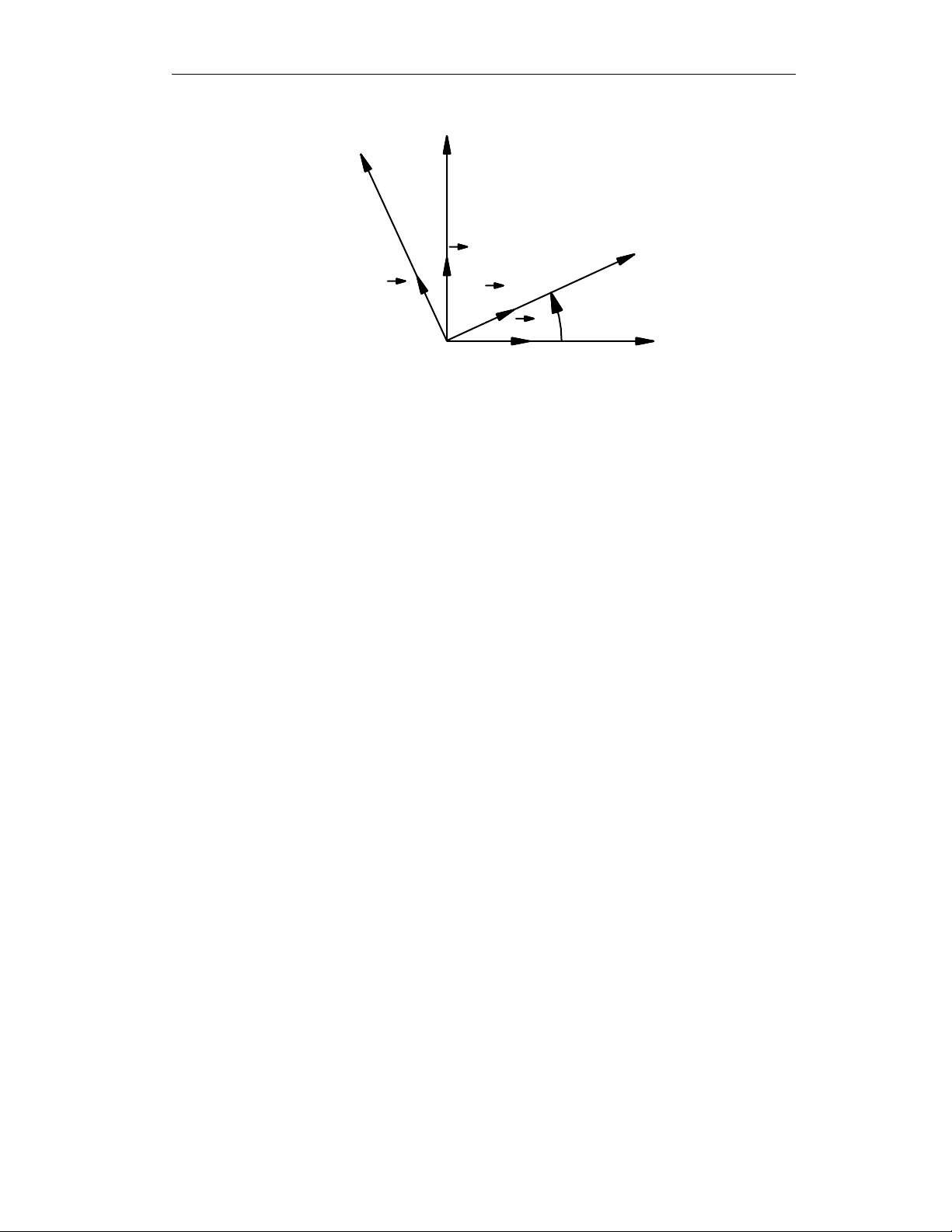
Ta tìm ma trận quay của phép quay quanh trục x0 một góc
ϕ
(Hình 2.4).
Chương 2 : Cơ sở lý thuyết chung về phân tích động học vật rắn không gian
- 5 -
Hình 2.4
Theo công thức định nghĩa (2.1) ta có:
0x
A
(0) (0) (0)
11 1 2 13
(0) (0) (0)
21 22 23
(0) (0) (0)
31 32 33
...
() . . .
...
eeee ee
eeee ee
eeee ee
ϕ
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
rrrr rr
rrrr rr
rrrr rr
(2.14)
0()
ϕ
x
A=
10 0
0cos sin
0sin cos
ϕ
ϕ
ϕ
ϕ
⎡⎤
⎢⎥
−
⎢⎥
⎢⎥
⎣⎦
(2.15)
Ma trận (2.15) được gọi là ma trận quay của phép quay cơ bản quanh trục x0.
Bằng cách tương tự, ta xác định được các ma trận quay cơ bản quanh các
trục y0 và z0 (Hình 2.5)
0()
ψ
=
y
A
cos 0 sin
010
sin 0 cos
ψ
ψ
ψ
ψ
⎡⎤
⎢⎥
⎢⎥
⎢⎥
−
⎣⎦
, 0()
θ
=
z
A
cos sin 0
sin cos 0
001
θ
θ
θθ
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
(2.16)
Từ các công thức (2.15) và (2.16) ta dễ dàng tính được:
000
det ( ) det ( ) det ( )
ϕ
ψθ
==
xyz
AAA (2.17)
e2
Z
Z
Y
O
0
0
Z
e2
(0)
e3
(0)
3
eϕ