SỞGIÁODỤC&ĐÀOTẠOBẮCNINH
TR¦êNG THPT THUËN THµNH Sè IIĐỀ kh¶o s¸t chÊt lîng «n thi ®¹i häcLẦN1
Nămhọc:2012 –2013
Môn thi:Toán,KhốiA,B,D
Thờigianlàmbài:180phút
a. phÇn chung cho tÊt c¶ c¸c thÝ sinh (7,0 ®iÓm)
CâuI(2,0điểm). Chohàmsố 1
2
+
+
=x
mx
y(1) (mlµ tham sè )
1. Khảosátsựbiếnthiênvàvẽđồthịhàmsốkhi 1 - =m.
2. Cho hai ®iÓm A ),4;3( - B( )2;3 - . T×m m ®Ó trªn ®å thÞ hµm sè (1) cã hai ®iÓm ph©n biÖt P, Q c¸ch ®Òu hai
®iÓm A, B vµ diÖn tÝch tø gi¸c APBQ b»ng 24.
CâuII(2,0điểm).
1. Giảiphươngtrình: ).sin1).(cos1(2
1cos
2sincos2cos2 3
xx
x
xxx + + =
-
- -
2. Gi¶i hÖ ph¬ng tr×nh: ï
î
ï
í
ì
= + + + - +
+ + + = + + +
44842)1(
36)2(4121
22
2
xyxxxx
yxyxyx ( ), Ryx Î .
CâuIII(1,0điểm). TÝnh tÝch ph©n sau : ò + +
-
=
-
3ln2
2ln2 2
2
2
)1)(1(
1dx
ee
e
I x
x
x
CâuIV(1,0 điểm).ChohìnhchópS.ABCDcó ®¸y ABCD lµ h×nh thang vu«ng t¹i A vµ D, AD = DC, AB = 2AD,
BC =2a . Tam gi¸c SBC c©n t¹i S vµ n»m trong mÆt ph¼ng vu«ng gãc víi ®¸y, SA hîp víi ®¸y mét gãc0
45 . TÝnh
thÓ tÝch h×nh chãp S.ABCD vµ kho¶ng c¸ch gi÷a hai ®êng th¼ng SA, BC thea a. .
CâuV(1,0 điểm) Choa,b,clàbasố thùc tho¶ m·n: abccbacba = + + + ³ ³ ³ 2,1,1,1 .
T×m gi¸ trÞ lín nhÊt cña biÓu thøc:c
c
b
b
a
a
P111 222 -
+
-
+
-
= .
b.PHẦNRIÊNG(3,0®iÓm). (ThÝ sinh chØ ®îc chän mét trong hai phÇn)
a.Phầndànhcho ch¬ng tr×nh chuÈn.
CâuVIa(2,0 điểm).
1. TrongmặtphẳngvớihệtäađộOxychotamgiácABC víi A ),2;3( - B(1; 0). Tam gi¸c ABC cã diÖn tÝch
b»ng 4 vµ b¸n kÝnh ®êng trßn ngo¹i tiÕp b»ng 2. T×m täa ®é ®Ønh C. BiÕt ®Ønh C cã tung ®é d¬ng.
2. Trongkhônggianvớihệtäa ®é Oxyz cho hai ®iÓm A )1;0;3( - , B )1;0;1( . T×m täa ®é c¸c ®iÓmCthuéc
mp(Oxy) sao cho tam gi¸c ABC c©n t¹i C vµ cã diÖn tÝch b»ng.24
CâuVIIa(1,0 điểm). Cho hai ®êng th¼ng song song1
d vµ d2 . Trªn ®êng th¼ng1
d cã 12 ®iÓm ph©n biÖt, trªn
®êng th¼ng d2 cã n ®iÓm ph©n biÖt ( n 2 ³ ). BiÕt r»ng cã 3.600 tam gi¸c cã ®Ønh lµ c¸c ®iÓm ®· cho. T×m n tho¶
m·n ®iÒu kiÖn.
b.Phầndànhchobannângcao.
CâuVIb(2,0 điểm).
1. Trong mÆt ph¼ng víi hÖ täa ®é Oxy cho (E): 1
28
22 = +yx . T×m bèn ®Ønh h×nh ch÷ nhËt n»m trªn (E). BiÕt
h×nh ch÷ nhËt nµy nhËn hai trôc täa ®é lµ hai trôc ®èi xøng vµ cã diÖn tÝch lín nhÊt.
2. TrongkhônggianvớihệtäađộOxyzcho h×nh vu«ng ABCD, biÕt A(3; 0; 8), C )0;4;5( - - , ®Ønh B cã tung
®é d¬ng vµ thuéc mÆt ph¼ng (Oxy). T×m täa ®é ®Ønh D.
CâuVIIb(1,0điểm). Gi¶i ph¬ng tr×nh: 6416
24
2.
)2(4 2
2
12
+ =
+ + +
- +
+
x
xx
x
x x
x
Cảmơntrangnguyenthi(truckhonghoa@gmail.com) gửitớiwww.laisac.page.tl
HƯỚNGDẪNCHẤM
Môn:Toán
Điểm
CâuI
(2điểm)
1.(1.0 đ)
*) Víi m = -1 hµm sè trë thµnh1
2
+
+ -
=x
x
y
1) TXĐ:RD =\
{ }
1 -
2)Sựbiếnthiên:
Chiềubiếnthiên: 1,0
)1(
3
2 - ¹ " <
+
-
= x
x
y ,
Hàmsốnghịchbiếntrên mỗikhoảng
( )
; 1 -¥ -và
( )
1;+¥.
Cựctrị:Hµm sè kh«ng cã cùc trÞ.
TiÖm cËn:
+¥ =
+
+ -
= -¥ =
+
+ -
= + + - - - ® - ® - ® - ®1
2
limlim,
1
2
limlim )1()1()1()1(x
x
y
x
x
y xxxx
Do ®ã, ®êng th¼ng1 - =x lµ tiÖm cËn ®øng.
1
1
2
limlim - =
+
+ -
= ±¥ ® ±¥ ®x
x
y xx .
Do ®ã, ®êng th¼ng 1 - =y lµ tiÖm cËn ngang.
Bảngbiếnthiên:
x ¥ 1 +¥
y’
y
1 +¥
¥ 1
3)Đồthị:
Đồthịhàmsốđiquacácđiểm (2; 0), (0;2)
VÏ ®å thÞ ®óng chÝnh x¸c th× cho ®iÓm tèi ®a.
0,25
0,25
0,25
0,25
2. Ta cã
+ ph¬ng tr×nh AB: 01 = + +yx ,26 =AB .
+ M(0; -1) lµ trung ®iÎm AB nªn ph¬ng tr×nh trung trùc AB lµ d: 1 - =xy .
+ Do P, Q c¸ch ®Òu hai ®iÓm A, B nªn P, Q thuéc ®êng th¼ng d.
+ Ph¬ng tr×nh hoµnh ®é giao ®iÓm cña d víi ®ths (1): (*),03
2 = - - mxx víi1 - ¹x
+ T×m ®kiÖn ®Ó d c¾t ®ths (1) t¹i 2 ®iÓm ph©n biÖt P, Q lµ2 ¹m
+ Ta cã P, Q thuéc d nªn gi¶ sö P babbQaa ¹ - - ),1,(),1,( . Víi a, b lµ hai nghiÖm cña (*)
+Theo ®Þnh lÝ viet ta cã î
í
ì
- =
= +
3.ba
mba
+ Theo gi¶ thiÕt diÖn tÝch tø g¸c APBQ b»ng 24 nªn ta ®îc PQ.AB = 48 mµ 2.baPQ - =
Suy ra164)(4 2 = - + Û = - abbaba24
2 ± = Þ = Þ mm . So s¸nh ®kiÖn ta ®îc2 - =m .
0.25
0,25
0,25
0,25
CâuII
(2®iÓm)
1(1.0 đ)
§K : cosx ¹ 1. §a vÒ pt d¹ng:
cosxsinx(sinx+1)=(1 cos x
2 )(1 + sinx) Û cosxsinx(sinx + 1) = sin x
2 (1 + sinx)
0)sin)(cos1(sinsin = - + Û xxxx .
+)sinx=0suyracosx= 1 ±so s¸nh ®k ta ®îc
p p
kxx 21cos + = Û - =
+)
p
p
kxx 2
2
1sin + - = Û - =(tm®k)
+)
p
p
kxxxx + = Û = Û = -4
1tan0sincos (tm®k).
VËy ph¬ng tr×nh cã 3 hä nghiÖm:
p
p
p
p
p p
kxkxkx + = + - = + =4
,2
2
,2
0,25
0,25
0.25
0,25
2(1.0đ)
§K: 2x + y0 ³ . Tõ ph¬ng tr×nh ban ®Çu cña hÖ ta ®îc:
0)124)(124(
1236
124
01)24()1236( 2 = + + - + +
+ + + +
- +
Û = - + + + + - + yxyx
yxyx
yx
yxyxyx
01)2(2
1236
1
)124( =
ú
ú
û
ù
ê
ê
ë
é + + +
+ + + +
- + Û yx
yxyx
yx (*).
0,25
Do 2x + y0 ³ nªn (*) t¬ng ®¬ng víi 1240124 = + Û = - + yxyx (1)
BiÕn ®æi ph¬ng tr×nh hai trong hÖ ta ®îc 04)24(242)1( 2 = - + + + - + yxxxxx (2).
Tõ (1) vµ (2) ta ®îc ph¬ng tr×nh: 04242)1( 2 = - + + - + xxxx (3)
XÐt hµm sè 4242)1()( 2 - + + - + = xxxxxf trªn R.
Ta cãRx
xx
xx
xx
xx
xxxf Î " > +
+ -
+ +
= +
+ -
- +
+ + - = 02
422
78
2
422
)14)(1(
42)( 2
2
2
2,
Suy ra hµm sè f(x) ®ång biÕn trªn R mµ0)
2
1
( =f nªn2
1
=x lµ nghiÖm duy nhÊt cña (3)
Víi)(
2
1
2
1tmdkyx - = Þ = . Thµnh thö hÖ cã nghiÖm)
2
1
;
2
1
();( - =yx
0,25
0,25
0,25
CâuIII
(1điểm) BiÕn ®æi ta cã dx
e
ee
I x
xx
ò +
-
=
3ln2
2ln2 2
2 )1(
)1( . §Ættdtdxeetet xx
x
2
2
2 = Þ = Þ =
§æi cËn víi 33ln2;22ln2 = Þ = = Þ = txtx
Ta ®îc ò ò ò +
+ - =
+
-
=
+
-
=
3
2
3
2
2
3
2
2
2
)
1
2
2(2
1
2
)1(
)1(
2 dt
t
tdt
t
tt
dt
t
tt
I
Suy ra3
2
3
2
3
2
2 1ln44 + + - = tttI
Tõ ®ã tÝnh ®îc3
4
ln41+ =I
0,25
0,25
0,25
0,25
CâuIV
(1điểm)
* TÝnh thÓ tÝch h×nh chãp S.ABCD
Gäi I lµ trung ®iÓm AB suy raIBC D vu«ng c©n t¹i I mµ2aBC =aDCADIAICIB = = = = = Þ
Tõ ®ã ta ®îc2
2
3
2
)(a
ADABDC
SABCD =
+
= (dvdt).
Gäi H lµ trung ®iÓm BC doSBC D c©n t¹i S ,BCSH ^ Þ mµ )()()( ABCDSHABCDSBC ^ Þ ^ ,
theo gi¶ thiÕt SA hîp víi ®¸y mét gãc0
45 suy ra gãc SAH b»ng0
45
Ta cãADC D vu«ng c©n t¹i D2aAC = Þ Tõ ®ã ta ®îcACB D vu«ng c©n t¹i C
aCHACAH2
5
22 = + = Þ . Tõ ®ã ta ®îc aAHSH2
5
= = . VËy3
. 4
10
.
3
1aSSHV ABCDABCDS = =
* TÝnh kho¶ng c¸ch gi÷a SA vµ BC theo a.
Trong mÆt ph¼ng ®¸y ABCD dùng h×nh b×nh hµnh ABHP, tõ H dùng APHQ ^ , trong (SHQ) ta dùng
SQHK ^ (1). Theo gi¶ thiÕt ta cãSHAP ^ do ®ã ta ®îc HKAPSHQAP ^ Þ ^ )( (2). Tõ (1) vµ (2)
ta ®îc )(SAPHK ^ .
MÆt kh¸c BC // AP nªn d(BC, SA) = d(BC, (SAP)) = d(H, (SAP)) = HK.
0,25
0,25
0,25
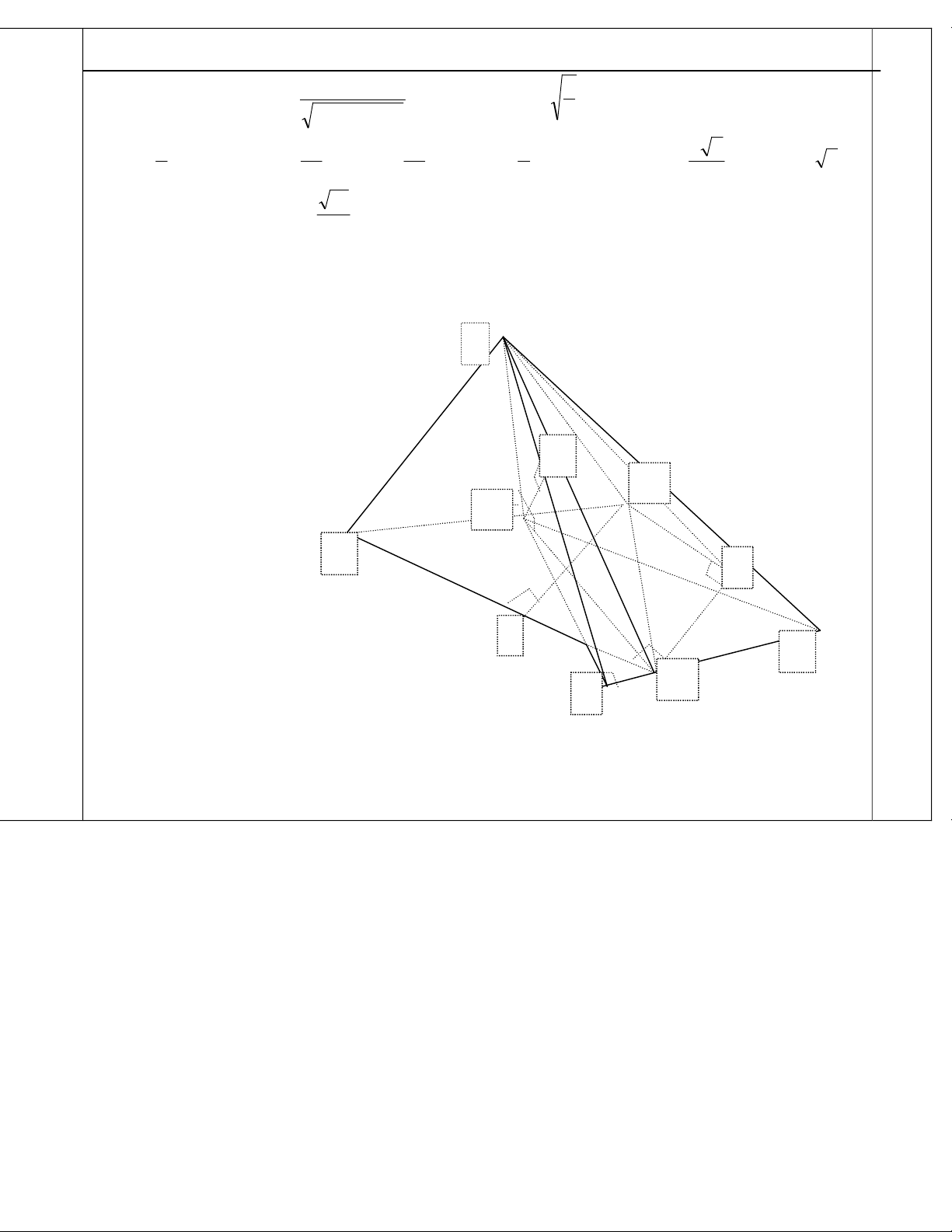
Trong SHQ D ta cã22
.
HQSH
HQSH
HK +
= , trong ®ã aSH2
5
= . Trong h×nh b×nh hµnh ABHP ta cã
22
45sin..
2
1 22
0a
S
a
BHABS AHPABH = Þ = =
D mµ2
2
,.
2
1 a
BHAPAPHQSAHP = = =2aHQ = Þ .
Suy ra aHKSABCd3
10
),( = =
(Kh«ng vÏ h×nh hoÆc vÏ h×nh sai kh«ng chÊm ®iÓm)
0,25
A
B
C
D
H
I P
Q
K
S
![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)
![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)
