
SỞ GIÁO DỤC - ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI TỈNH
THỪA THIÊN HUẾ KHỐI 12 THPT _ NĂM HỌC 2011 - 2012
Môn : TOÁN
ĐỀ CHÍNH THỨC Thời gian làm bài: 180 phút (không kể thời gian giao đề)
Bài 1: (3 điểm)
Cho hàm số f(x) = x3 - 2x2 – (m - 1)x + m (C)
a). Tìm m để đồ thị (C) tiếp xúc với trục hoành.
b). Tìm m để
1
f(x)
x
với mọi
x 2
Bài 2: (4 điểm)
a) Giải phương trình sau : 2 2
3 (2 9 3) (4 2)( 1 1) 0
x x x x x
b) Giải phương trình sau : 4 2 4 2
1 1 9 3 1
+ cos x - cos x + + cos x - cos x =
16 2 16 2 2
Bài 3: (3 điểm)
Chứng minh rằng : n
2n
2n
1 1
C < ( n ; n 1)
22n+1
Bài 4: (3 điểm)
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, có tâm I thuộc
đường thẳng (d) : x – y – 3 = 0 và có hoành độ bằng I
9
x =
2
, trung điểm của một
cạnh là giao điểm của đường thẳng (d) với trục hoành. Tìm tọa độ đỉnh của hình chữ
nhật.
Bài 5: (5 điểm)
Cho hình lăng trụ đứng ABC.A’B’C’, đáy ABC vuông tại A. Khoảng cách từ AA’ đến
mặt phẳng BCC’B’ là a, mặt phẳng (ABC’) cách C một khoảng bằng b và hợp với đáy
một góc bằng
.
a). Tính thể tích của khối lăng trụ.
b). Cho a = b không đổi, còn
thay đổi. Định
để thể tích khối lăng trụ nhỏ nhất.
Bài 6: (2 điểm)
Tính giới hạn :
cotx cotx cotx cotx
0
A = lim[ ln (1 tanx) (1 tanx) (1 tanx) .....
(1 tanx) ...... ]
x
v« h¹n dÊu c¨n
(1)
__________Hết__________
Giám thị coi thi không giải thích gì thêm

1
Së Gi¸ o d ô c - § µ o t ¹ o Kú t h i c h ä n h ä c sin h g iá i t Øn h
Th õa Th iª n Hu Õ Kh è i 12 THPT - N¨ m h ä c 2011 - 2012
CHÍNH THỨC MÔN TOÁN
ĐÁP ÁN – THANG ĐIỂM
Bài NỘI DUNG ĐIỂ
M
Bài 1
Cho hàm số f(x) = x
3
- 2x
2
– (m - 1)x + m (C) (3đ)
a). Tìm m để đồ thị (C) tiếp xúc với trục hoành.
1.0đ
f(x) tiếp xúc với trục hoành
f(x) = 0
f (x)=0
3 2
2
x - 2x - (m -1)x + m = 0 (a)
3x - 4x + 1= 0 (b)
0.5
Từ (a) và (b) ta có : 2x
3
- 5x
2
+ 4x – 1 = 0.
2
(x - 1) (2x - 1) = 0
x = 1 m = 0
1 1
x = m = -
2 4
0.5
b). Tìm m để
1
f(x)
x
với mọi
x 2
2.0đ
1
f(x)
x
với mọi
x 2
3 2
1
x - 2x - (m - 1)x + m
x
2
x(x - 1)(x - x - m) 1
2
2
1
m x - x -
x - x
0.5
Đặt t = x2 – x thì 2
t 1
m
t
Khi
x 2 t 2
(vì 2
x 2 t = g(x) = x - x
là hàm số tăng và g(2) =
2 )
Xét 2
t 1 1
y = = t -
t t
với
t 2
2
2 2
1 t + 1
y = 1 + = > 0
t t
1.0
x 2
y’ +
y
3
2
Vậy
3
m
2
0.5
Bài 2
(4đ)
2
a) Giải phương trình: 2 2
3 (2 9 3) (4 2)( 1 1) 0
x x x x x
(1) 2.0
Ta thấy pt chỉ có nghiệm trong
1
( ;0)
2
2 2
2 2
3 (2 ( 3 ) 3) (2 1)(2 (2 1) 3)
(2 3) (2 3) (1)
pt x x x x
u u v v
Với u = - 3x, v = 2x + 1; u,v >0.
1.0
Xét hàm số
4 2
( ) 2 3
f t t t t
với t>0
Ta có 3
4 2
2 3
'( ) 2 0 0 ( ) ( )
3
t t
f t t f u f v u v
t t
- 3x = 2x + 1
1
5
x
là nghiệm duy nhất của phương trình
1.0
b) Giải phương trình sau :
4 2 4 2
1 1 9 3 1
+ cos x - cos x + + cos x - cos x =
16 2 16 2 2
(1)
2.0
2 2 2 2
2 2
1 3 1
(1) (cos x - ) + (cos x - ) =
4 4 2
1 3 1
cos x - + cos x - =
4 4 2
Đặt cos2x = t ; 0 ≤ t ≤ 1
1 3 1
t - + t - =
4 4 2
Xét trên trục Ox, các điểm : M(t) ; A(
1
4
) ; B(
3
4
)
Suy ra : MA + MB =
1
2
1.0
Mà AB =
1
2
, nên M nằm giữa A và B, suy ra
1
4
≤ t ≤
3
4
.
1 3
cos x
2 2
π + kπ x + kπ
6 3
(l;k )
π + lπ x - - lπ
3 6
1.0
Bài 3
Chứng minh rằng : n
2n
2n
1 1
C < ( n ; n 1)
22n+1
(3đ)
Ta có :
n
2n
2n 2n n n n n
1 (2n)! 1.2.3.4.......(2n - 1).(2n) 1.3.5..
.(2n - 1).2.4.6...(2n)
C = =
2 2 .n!n! 2 .2 .(1.2.3.4...n).(1.2.3.4...n)
2 .(1.2.3.4...n).2 .(1.2.3.4...n)
1.3.5.7.....(2n - 1)
= 2.4.6.8...
....(2n)
1.0

3
Ta chứng minh : 1.3.5.7.....(2n - 1) 1
<
2.4.6.8.......(2n)
2n+1
Ta có :
2 2
2 2
(2k - 1) (2k - 1)
(2k - 1) 2k - 1
= = < =
(2k)
2k + 1
(2k) 4k - 1
1.0
Sử dung quy nạp và nhân các BĐT vế theo vế ta có :
1.3.5.7.....(2n - 1) 1
<
2.4.6.8.......(2n)
2n+1
(đpcm)
1.0
Bài 4
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, có
tâm I thuộc đường thẳng (d) : x – y – 3 = 0 và có hoành độ bằng I
9
x =
2
,
trung điểm của một cạnh là giao điểm của đường thẳng (d) với trục
hoành. Tìm tọa độ đỉnh của hình chữ nhật.
(3 đ)
Điểm I có I
9
x =
2
và I thuộc đường thẳng (d) : x – y – 3 = 0
9 3
I( ; )
2 2
Vì vai trò của A; B; C; D là như nhau nên giả sữ trung điểm M của cạnh AD
là giao điểm của (d) với trục Ox, suy ra M(3;0)
9 9
AB = 2IM = 2 =3 2
4 4
1.0
ABC
ABC
12
AB.AD = 12 AD = 2 2
AB 3 2
S
S
AD (d)
M AD
suy ra phương trình AD : x + y – 3 = 0
1.0
Mặt khác MA = MD =
2
. Vậy tọa độ A; D là nghiệm vủa hệ phương trình :
2 2
x + y - 3 = 0
x = 2 x = 2
y = 1 y = -1
(x - 3) + y = 2
hoÆc
Vậy A(2; 1), D(2; -1).
9 3
I( ; )
2 2
là trung điểm AC và BD nên C(7; 2) và B(4; - 1)
1.0
Bài 5
Cho hình lăng trụ đứng ABC.A’B’C’, đáy ABC vuông tại A. Khoảng cách
từ AA’ đến mặt phẳng BCC’B’ là a, mặt phẳng (ABC’) cách C một
khoảng bằng b và hợp với đáy một góc bằng
.
(5đ)
a). Tính thể tích của khối lăng trụ. 3.0
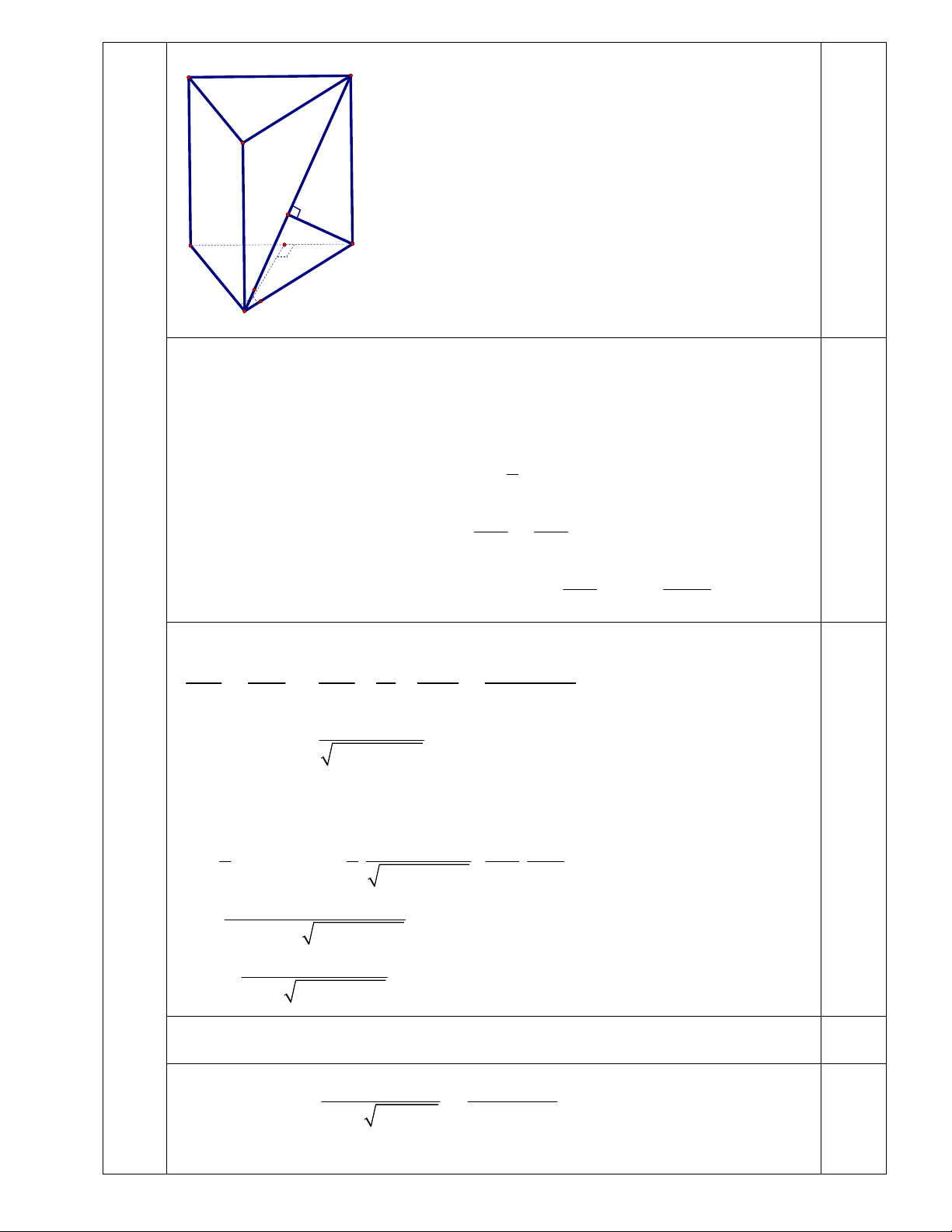
4
Ta có AA’ || ( BCC’B’), kẻ AH
BC (
H BC
)
AH
( BCC’B’)
vì (ABC)
( BCC’B’), do đó : AH = d(AA’,(
BCC’B’)) = a.
Ta có AB = (ABC’) (ABC) ; AB
AC (gt) ; AC
là hình chiếu của AC’ trên (ABC)
AB
AC’
CAC sd((ABC),(ABC )) =
( góc nhọn).
1.0
Kẻ CK
AC’; ta có : AB
(ACC’) (ABC’)
(ACC’) ;
AC’ = (ABC’)(ACC’)
AK
(ABC’) CK = d(C,( ABC’)) = b.
Thể tích khối lăng trụ : V = ABC
1
.CC = AB.AC.CC
2
S
(1)
Trong tam giác vuông ACK :
CK b
AC = =
sin
α sinα
Trong tam giác vuông ACC’ : b b
CC = AC.tan
α = .tanα
sin
α cosα
1.0
Trong tam giác vuông ABC :
2 2 2 2
2 2 2 2 2 2 2
1 1 1 1 sin
α b a sin α
= = - =
AB AH AC a b a b
2 2 2
ab
AB = b a sin
α
Thay các kết quả vào (1) ta có :
2 2 2
3
2 2 2
3
2 2 2
1 1 ab b b
V = AB.AC.CC = . . .
2 2 sin
α cosα
b a sin α
ab
= 2sinαcosα b a sin α
ab
V = sin2α b a sin α
1.0
b). Cho a = b không đổi, còn
thay đổi. Định
để thể tích khối lăng trụ
nhỏ nhất.
2.0
Với a = b : 3 3
2
2
a a
V = 2sin
α.cos α
sin2α 1 sin α
V nhỏ nhất khi sin
.cos2
lớn nhất .
1.0
_
a
_
b
_
K
_
A
'
_
C
'
_
B
_
A
_
C
_
B
'
_
H


![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








