
Tailieumontoan.com
Sưu tầm
CHUYÊN ĐỀ
THỂ TÍCH KHỐI LĂNG TRỤ ĐỨNG
Tài liệu sưu tầm, ngày 24 tháng 8 năm 2020
Website: tailieumontoan.com
KIẾN THỨC CẦN NHỚ:
Thể tích khối lăng trụ:
.V Bh
với
:B
diện tích đáy,
h
: chiều cao.
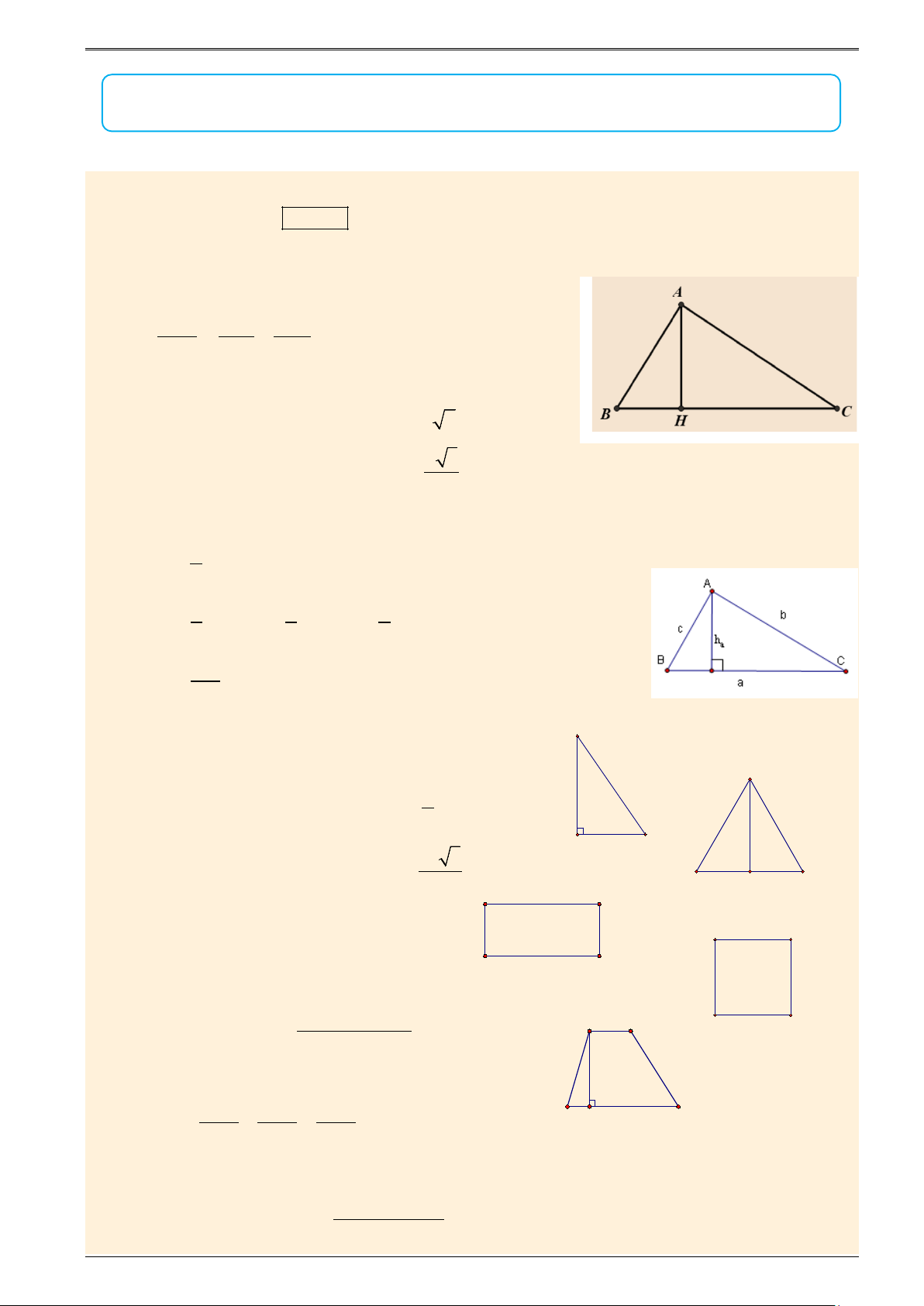
Các hệ thức lượng trong tam giác vuông
ABC
tại
A
có đường cao
AH
:
▪
222
BC AB AC
.
▪
222
111
AH AB AC
.
▪
2
.BH BC AB
,
2
.CH CB CA
.
Đường chéo của hình vuông cạnh
a
bằng
2a
.
Đường cao của tam giác đều cạnh
a
bằng
3
2
a
.
Diện tích tam giác thường:
▪
1.
2
a
S ah
.(
a
h
,
b
h
,
c
h
lần lượt là các đường cao hạ từ đỉnh
A
,
B
,
C
).
▪
111
sin sin sin
222
S ab C ac B bc A
.
▪
4
abc
SR
(
R
: bán kính đường tròn ngoại tiếp
ΔABC
).
▪
S pr
(
r
: bán kính đường tròn nội tiếp
ΔABC
).
Trường hợp đặc biệt :
▪ Diện tích tam giác vuông :
Δ
1.
2
ABC
S AB AC
▪ Diện tích của tam giác đều cạnh a :
23
4
a
.
Diện tích hình chữ nhật :
ab
.
Diện tích của hình vuông :
2
a
.
Diện tích hình thoi :
.S ABC
(
AC
và
BD
là hai đường chéo).
Diện tích hình thang:
()
2
AB CD AH
S
.
Diện tích hình bình hành:
ah
(
a
: đáy;
h
: chiều cao).
Định lí sin:
2
sin sin sin
abc
R
ABC
= = =
Định lí côsin:
2 22
2 cosa b c bc A
;
2 22
2 cosb a c ac B
;
222
2 cosc b a ab C
.
Công thức trung tuyến:
2 22
2
22
4
a
b ca
m
.
DẠNG TOÁN 4: TÍNH THỂ TÍCH KHỐI LĂNG TRỤ ĐỨNG
B
A
C
H
A
B
C
a
b
C
A
D
B
a
C
B
A
D
A
B
D
C
H
Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 Trang 1
Website: tailieumontoan.com
BÀI TẬP MẪU
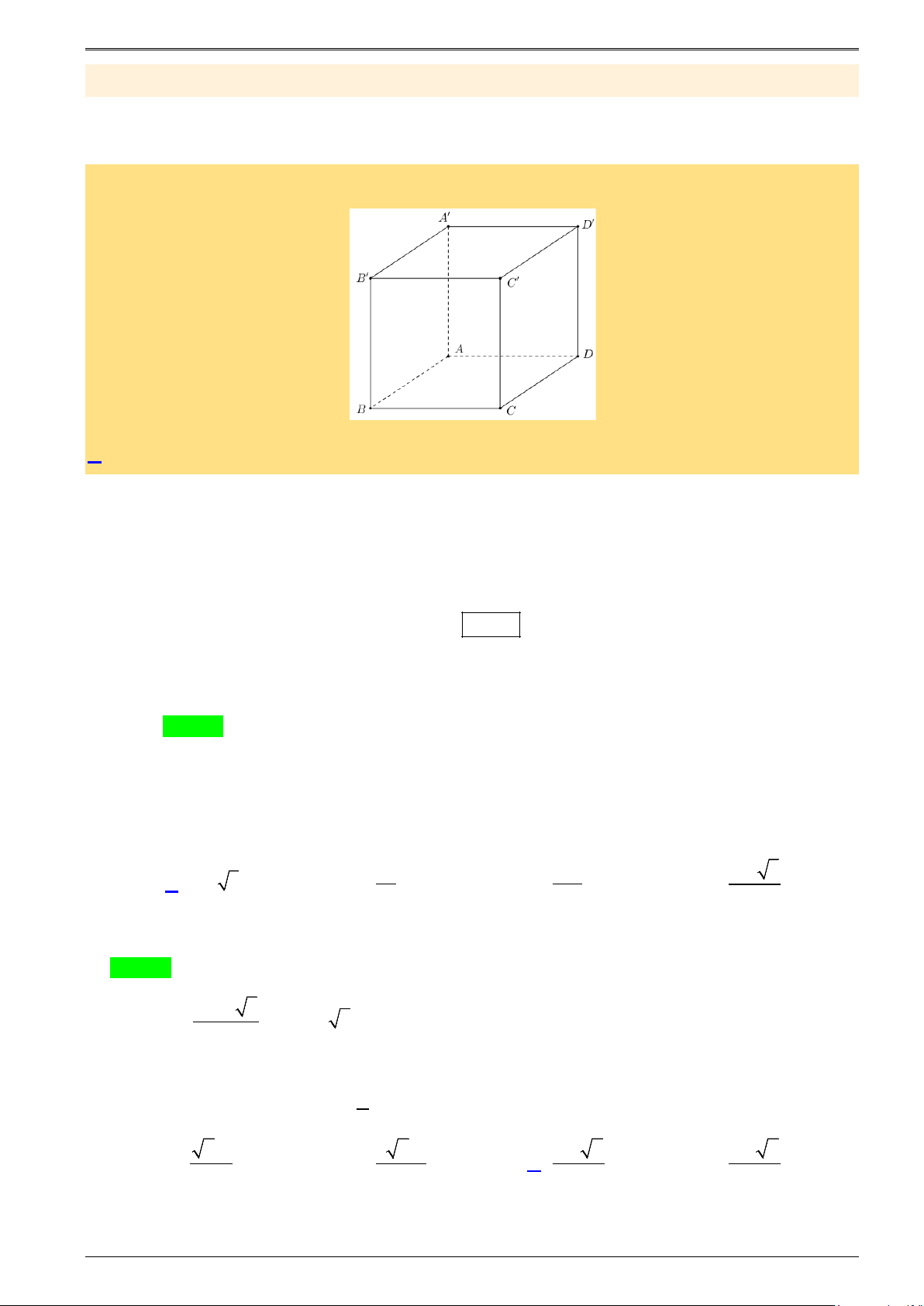
(ĐỀ MINH HỌA LẦN 2-BDG 2019-2020) Thể tích của khối lập phương cạnh bằng 2:
A. 6. B. 8. C. 4. D. 2.
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tính thể tích khối lăng trụ đứng.
2. HƯỚNG GIẢI:
Nhắc lại công thức tính thể tích khối lập phương:
3
Va
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn B
Thể tích của khối lập phương cạnh 2 bằng
3
28
.
Bài tập tương tự và phát triển:
Câu 4.1: Cho hình lăng trụ tam giác đều có các cạnh đều bằng
2a
. Thể tích khối lăng trụ đều là:
A.
3
23a
. B.
3
3
a
. C.
3
23
a
. D.
3
23
3
a
.
Lời giải
Chọn A
23
(2 ) 3
. .(2 ) 2 3
4
a
V Bh a a
.
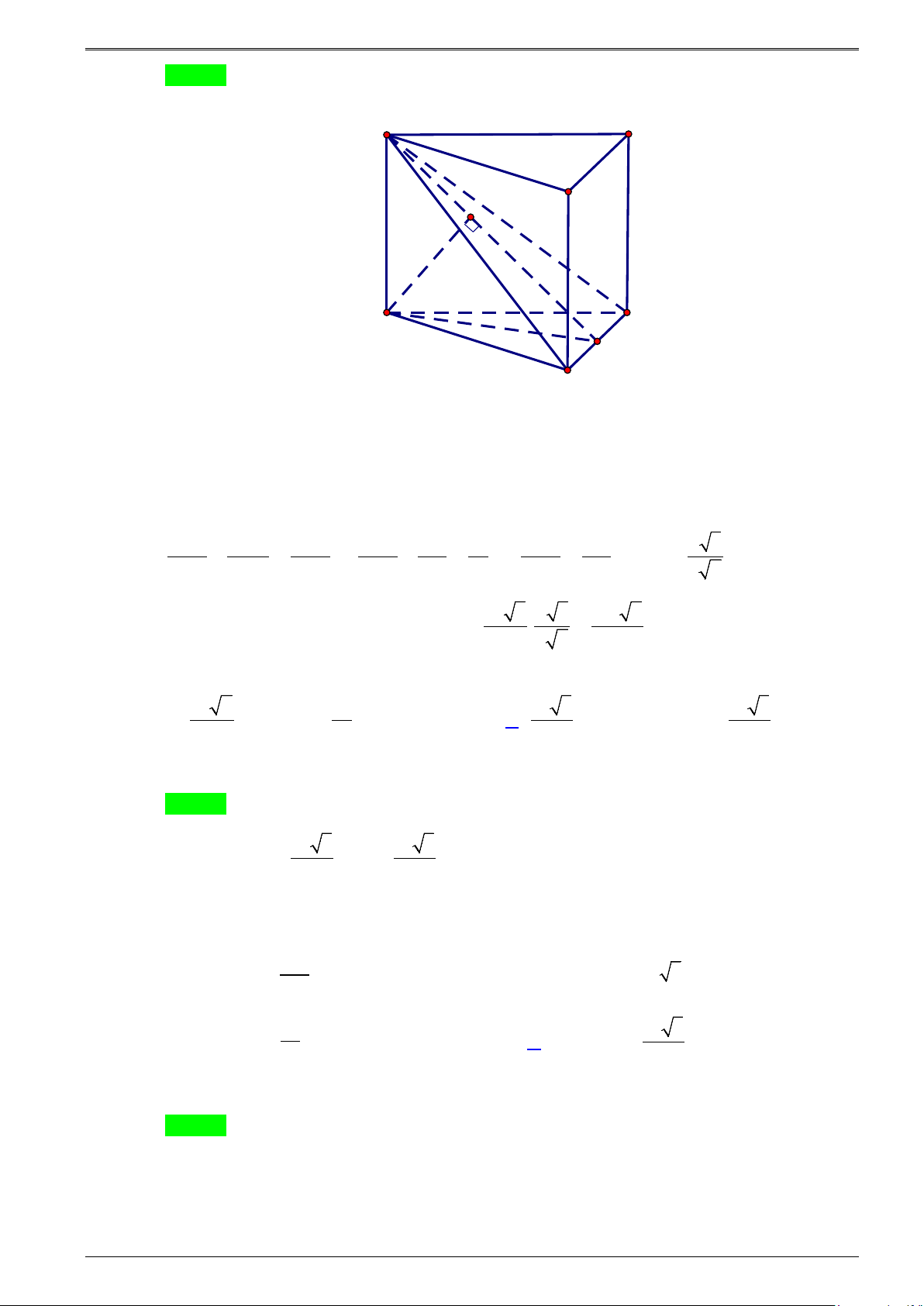
Câu 4.2: Cho khối lăng trụ tam giác đều
.ABC A B C
có cạnh đáy là
a
và khoảng cách từ
A
đến
mặt phẳng
A BC
bằng
2
a
. Tính thể tích của khối lăng trụ
.ABC A B C
.
A.
3
2
16
a
. B.
3
32
12a
. C.
3
32
16
a
. D.
3
32
48
a
.
Lời giải
Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 Trang 2
Website: tailieumontoan.com
Chọn C
Gọi
M
là trung điểm
BC
,
H
là hình chiếu của
A
trên
AM
. Nhận xét
,d A A BC AH
.
Tam giác
AA M
vuông tại
A
nên có:
222
111
A A AM AH
2 22
1 44
3AA a a
22
18 3
322
a
AA
AA a
.
Thể tích của lăng trụ
.ABC A B C
là
23
3 33 2
.
4 16
22
aa a
V
.
Câu 4.3: Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
bằng:
A.
3
2
3
a
. B.
3
3
a
. C.
3
3
4
a
. D.
3
3
6
a
.
Lời giải
Chọn C
Diện tích đáy là
23
33
44
aa
V
.
Câu 4.4: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
AB
tạo
với đáy một góc
0
45
Thể tích khối lăng trụ
.ABC A B C
là:
A.
3
.'''
23
ABC A B C
a
V
. B.
3
.'''
3
ABC A B C
Va
.
C.
3
.''' 6
ABC A B C a
V
. D.
3
.'''
3
4
ABC A B C
a
V
.
Lời giải
Chọn D
Ta có
AB
là hình chiếu vuông góc của
AB
lên
mp( )ABC
.
M
A
B
C
A'
B'
C'
H
Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 Trang 3
Website: tailieumontoan.com
0
,( ) 45A B ABC ABA
.
Khi đó tam giác
ABA
vuông cân tại
A AA AB a
.
Vậy
23
ABC.A B C
33
.
44
aa
Va
chọn phương án D.
Câu 4.5: Cho hình lăng trụ tứ giác đều
.ABCD A B C D
có cạnh đáy bằng
a
. Biết đường chéo của
mặt bên là
3a
. Khi đó, thể tích khối lăng trụ bằng:
A.
3
2a
. B.
3
3a
. C.
32a
. D.
32
3
a
.
Lời giải
Chọn B.
Ta có
AB a
,
3AB a
2
AA a
.
0
AA' .tan60
AC
23
..2
ABCD A B C D
V AA AB a
.
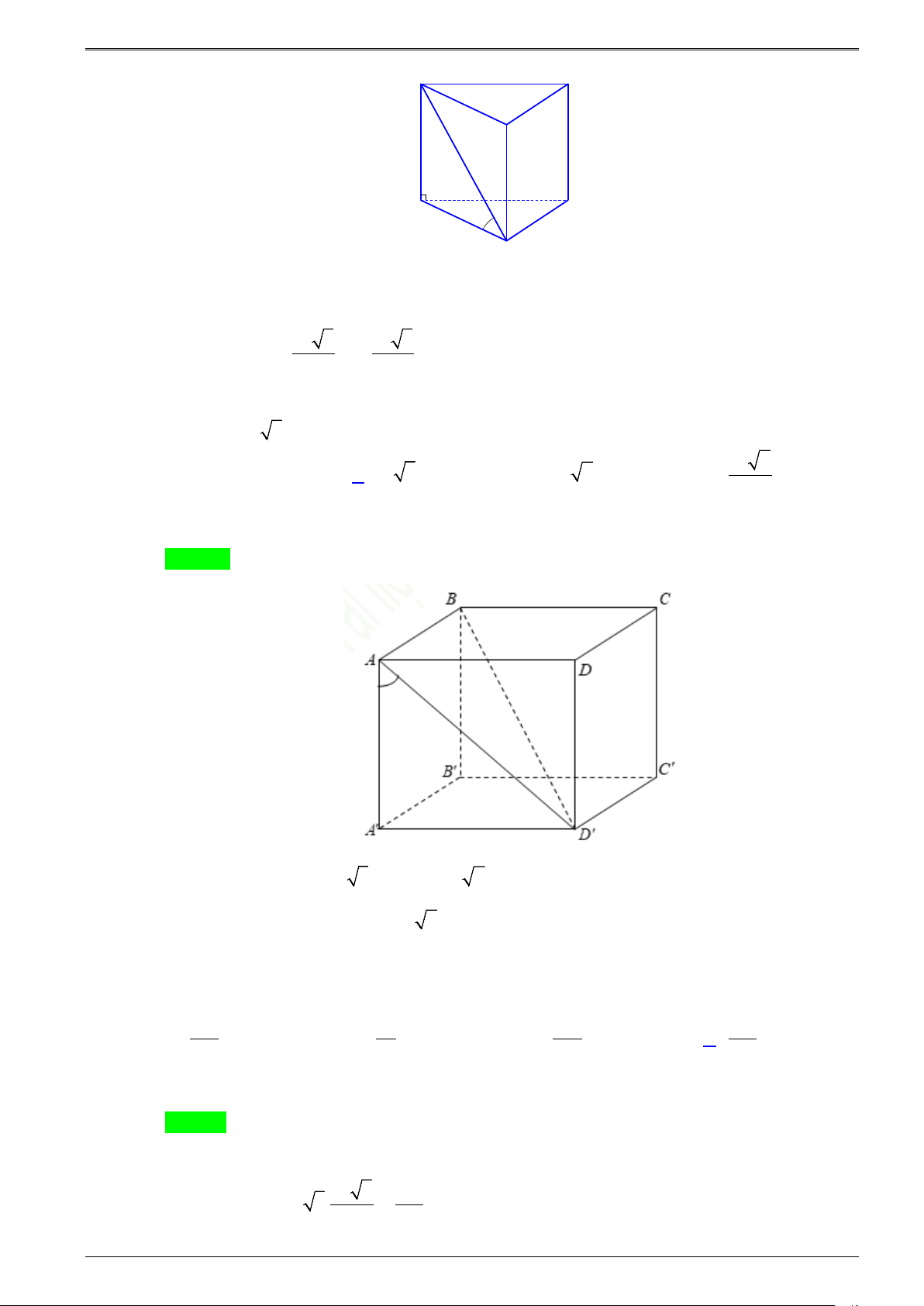
Câu 4.6: Cho hình lăng trụ đều
.ABC A B C
có cạnh đáy bằng
a
,
AC
hợp với mặt đáy
ABC
một
góc
60
. Thể tích của khối lăng trụ
.ABC A B C
bằng:
A.
3
38
a
. B.
3
4
a
. C.
3
23
a
. D.
3
34
a
.
Lời giải
Chọn D
0
AA' .tan60AC
.
23
33
' . 3. 44
ABC
aa
V A AS a
.
45
0
A
B
C
A′
B′
C′
Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 Trang 4


























