ĐỀ KIỂM TRA HỌC KÌ I
Môn: TOÁN - LỚP 12
Thời gian: 90 phút (không kể thời gian giao đề)
I. PHẦN CHUNG CHO TẤT CẢ HỌC SINH: ( 7 ĐIỂM )
Câu I: (2 điểm)
Cho hàm số y = x3 - 3x2 + 5 (1)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2. Dựa vào đồ thị (C) của hàm số (1), tìm tham số m để phương trình:
23t - 3.4t + 5 = m (t là ẩn) có nghiệm.
Câu II: (2 điểm)
1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x4 - 8x2 + 15 trên đoạn [-1; 3].
2. Tính đạo hàm của các hàm số sau:
a) y = x2.e4x b) y = ex.ln(2 + sinx)
Câu III: (1 điểm)
Giải các phương trình sau:
1) 2
x x 1
4 64
. 2) 3 3
log x log (x 2) 1
Câu IV: (2 điểm)
Cho hình lăng trụ đều tứ giác ABCD.A’B’C’D’ có độ dài cạnh đáy là 2a, cạnh bên là a.
1. Chứng minh hai khối tứ diện ABDA’ và CBDC’ bằng nhau.
2. Tính theo a thể tích của khối lăng trụ ABCD.A’B’C’D’.
3. Gọi M là trung điểm của cạnh A’D’, S là tâm của hình vuông ABCD. Tính theo a thể
tích của khối chóp S.MB’C’D’.
II. PHẦN RIÊNG: ( 3 ĐIỂM )
A. Phần dành cho học sinh học theo sách Toán 12 nâng cao
Câu Va: (3 điểm)
1. Viết phương trình tiếp tuyến của đồ thị hàm số
2
x x 2
y
x 2
biết tiếp tuyến song song
với đường thẳng 3x + y - 2 = 0.
2. Giải phương trình:
2
6 ln x
2 2
.
3. Cho hình chóp đều tứ giác S.ABCD có tất cả các cạnh đều bằng
a 2
. Tính theo a diện
tích của mặt cầu và thể tích của khối cầu ngoại tiếp hình chóp S.ABCD đã cho.
B. Phần dành cho học sinh học theo sách Toán 12 chuẩn
Câu Vb: (3 điểm)
1. Viết phương trình tiếp tuyến của đồ thị hàm số
x 4
y
x 1
biết tiếp tuyến song song với
đường thẳng 3x - 4y = 0.
2. Giải phương trình:
2x xlog 2
6 2 5.10 .
3. Cho hình chóp đều tứ giác S.ABCD có tất cả các cạnh đều bằng
a 2
. Tính theo a diện
tích xung quanh và thể tích của hình nón ngoại tiếp hình chóp S.ABCD đã cho.
………. Hết ……….
ĐÁP ÁN - THANG ĐIỂM
Câu
Nội dung Điểm
I 2,00
1 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = x
3
- 3x
2
+ 5.
1. Tập xác định:
฀
.
2. Sự biến thiên:
a)Giới hạn tại vô cực:
3
3 3
x x x x
3 5 3 5
lim y lim x (1 ) ; lim y lim (1 )
x x x x
   
 
.
0,25
b) Bảng biến thiên:
y’ = 3x2 - 6x = 3x(x - 2); y’ = 0 x = 0 hoặc x = 2 0,25
BBT: x -
0 2 +
y’ + 0 - 0 +
5 +
y -
1
Hàm số đồng biến trên (-; 0) và (2; +); nghịch biến trên (0; 2).
x
CT
= 2, y
CT
= 1; x
CĐ
= 0, y
CĐ
= 5.
0,50
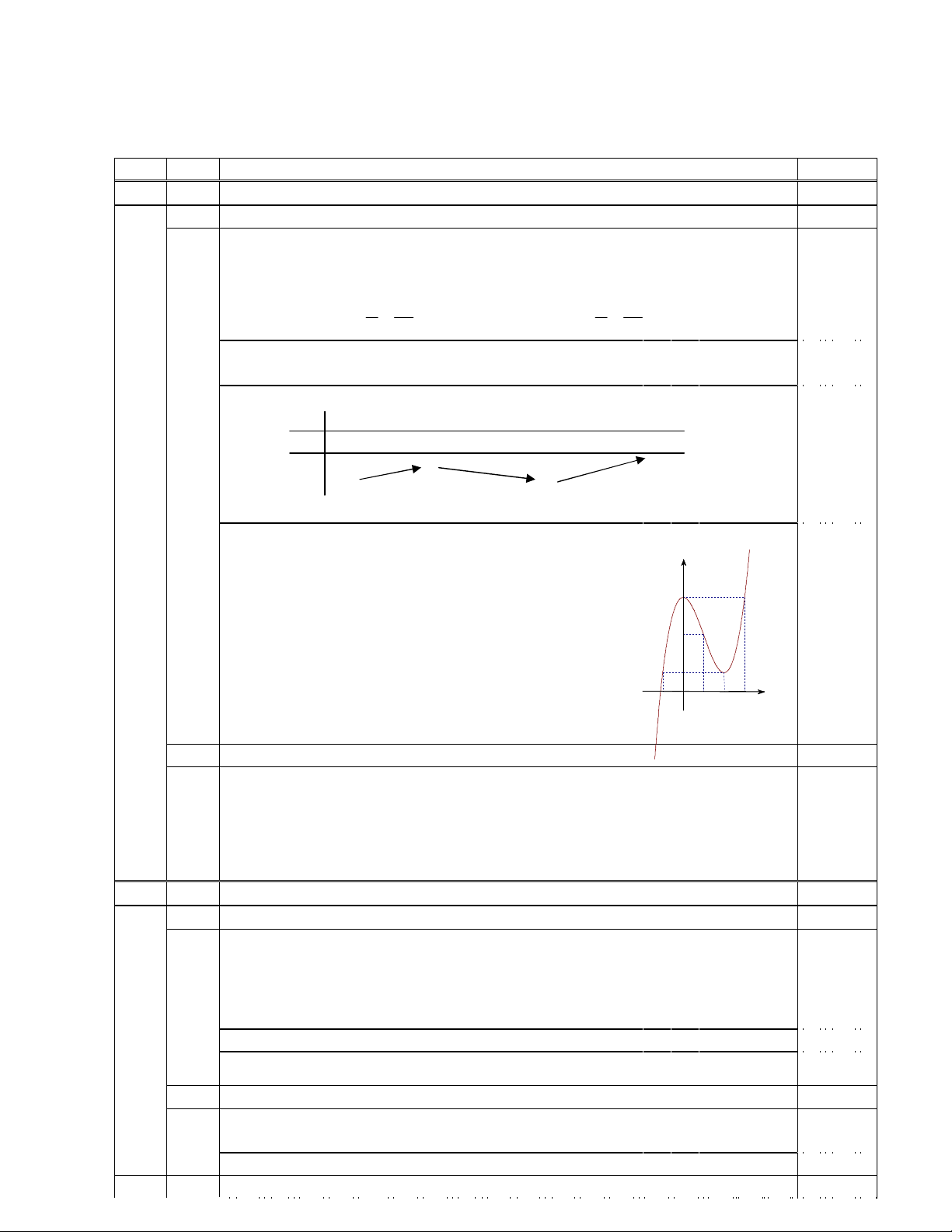
3. Đồ thị:
y’’ = 6x - 6; y’’ = 0 x = 1.
- Đồ thị nhận điểm uốn I(1; 3) làm tâm đối xứng.
- Đồ thị đi qua (-1; 1), (3; 5).
0,50
2 Dựa vào đồ thị (C) …..
Đặt x = 2
t
> 0, phương trình đã cho thành: x
3
- 3x
2
+ 5 = m.
Vậy phương trình đã cho có nghiệm khi và chỉ khi đường thẳng y = m có
điểm chung với đồ thị (C) của hàm số (1) trên khoảng (0; +).
Dựa vào đồ thị (C) của hàm số (1) trên khoảng (0; +) ta có các giá trị
của m cần tìm là: m 1.
0,50
II 2,00
1 Tìm giá trị nhỏ nhất và …..
Hàm số y = x
4
- 8x
2
+ 15 liên tục trên đoạn [-1; 3].
Ta có y’ = 4x3 - 16x = 4x(x2 - 4).
2
y ' 0 x 0, x 2 x 0
4x(x 4) 0
1 x 3 1 x 3 x 2
1 x 3
0,50
y(-1) = 8; y(0) = 15; y(2) = -1; y(3) = 24. 0,25
Vậy [-1; 3] [-1; 3]
Min y y(2) 1; Max y y(3) 24
. 0,25
2 Tính đạo hàm của các hàm số:
a) y = x
2
.e
4x
. Tập xác định:
฀
.
y’ = (x2)’.e4x + x2.(e4x)’. 0,25
= 2x.e
4x
+ x
2
.(4x)’.e
4x
= 2x.e
4x
(1 + 2x). 0,25
b) y = e
x
.ln(2 + sinx). Tập xác định:
฀
. 0,25
y
x
5
2 3 -1
O
3
1
1
y’ = (e
x
)’.ln(2 + sinx) + e
x
.(ln(2 + sinx))’
= ex.ln(2 + sinx) + ex.
(2 s inx)'
2 s inx
= ex.ln(2 + sinx) + ex.
cosx
2 sinx
0,25
III 1,00
1 Giải phương trình: 2
x x 1
4 64
.
Tập xác định:
฀
.
2
x x 1
4 64
2
x x 1 3
4 4
0,25
x
2
- x + 1 = 3
x = -1 hoặc x = 2. 0,25
2 Giải phương trình: 3 3
log x log (x 2) 1
.
Tập xác định: (2; +
).
3 3
log x log (x 2) 1
3
log [x(x 2)] 1
0,25
x(x - 2) = 3
x
2
- 2x - 3 = 0
x = -1 hoặc x = 3.
Vậy phương trình có nghiệm là x = 3. 0,25
IV 2,00
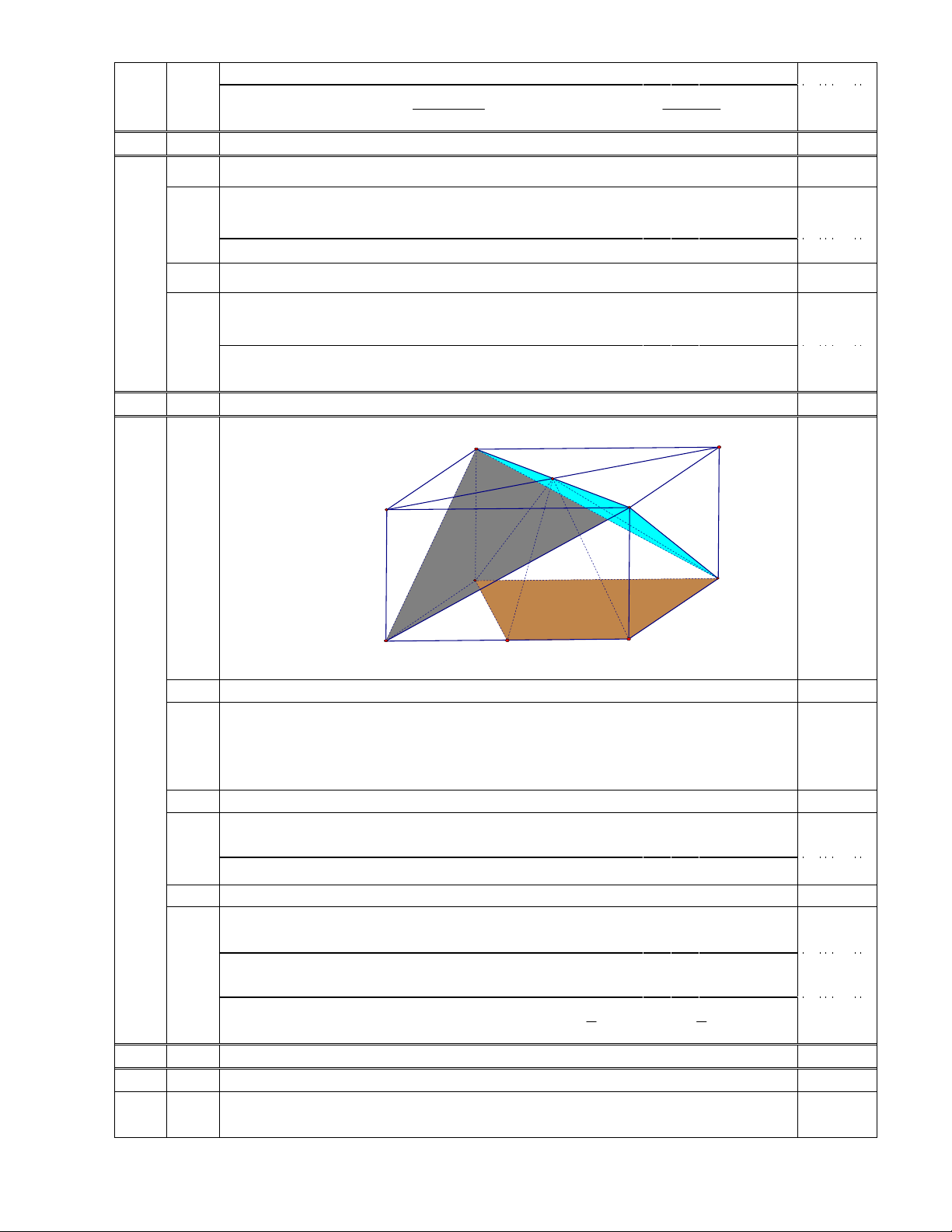
Hình vẽ
0,25
1 Chứng minh Chứng minh hai khối tứ diện ABDA’ và CBDC’ bằng nhau.
Ta có mp(BDD’B’) là mặt trung trực của hai đoạn thẳng AC và A’C’ nên
phép đối xứng qua mp(BDD’B’) biến bốn điểm A, B, D, A’ lần lượt
thành bốn C, B, D, C’.
Vậy hai khối tứ diện ABDA’ và CBDC’ bằng nhau.
0,25
2 Tính theo a thể tích của khối lăng trụ ABCD.A’B’C’D’.
Ta có đáy của khối lăng trụ là hình vuông ABCD có diện tích bằng 2a.2a
= 4a2. Chiều cao của khối lăng trụ bằng AA’ = a. 0,25
Vậy thể tích của khối lăng trụ là V = ABCD
S .AA'
= 4a
2
.a = 4a
3
0,50
3 Tính theo a thể tích của khối chóp S.MB’C’D’.
Ta có đáy của khối chóp S.MB’C’D’ có diện tích bằng:
S
MB’C’D’
= S
A’B’C’D’
- S
A’B’M
= 4a2 - a2 = 3a2. 0,25
Chiều cao của khối chóp S.MB’C’D’ bằng khoảng cách từ S đến
mp(A’B’C’D’) và bằng AA’ = a. 0,25
Vậy thể tích của khối chóp S.MB’C’D’ là V =
2 3
MB'C 'D'
1 1
S .AA' = .3a .a a
3 3
.
0,25
Va Phần dành cho học sinh học theo sách Toán 12 nâng cao 3,00
1 Viết phương trình tiếp tuyến …..
Tiếp tuyến
song song với đường thẳng 3x + y - 2 = 0 nên có hệ số góc
k = -3. Gọi (x
0
; y
0
) là tọa độ tiếp điểm, ta có k = -3 = y’(x
0
). 0,25
2a
a
M
S
C
D
A
D'
B' C'
A'
B
y = 2
4 4
x 3 y ' 1 , x 2
x 2 (x 2)
.
y’(x
0
) = -3 (x
0
+ 2)2 = 1 x
0
= -1 hoặc x
0
= -3.
0,25
Với x
0
= -1, y
0
= 0, ta có tiếp tuyến tại (-1; 0) là y = -3(x + 1). 0,25
Với x
0
= -3, y
0
= -10, ta có tiếp tuyến tại (-3; -10) là y = -3(x + 3) - 10. 0,25
2 Giải phương trình:
2
6 ln x
2 2
.
Điều kiện xác định của phương trình: x > 0.
2
6 ln x
2 2
2 2
6 ln x 5 6 ln x 5
2 2
log e log x e x
. 0,25
2 5 2
6 ln x ln x ln x 5ln x 6 0
lnx = 2 hoặc lnx = 3. 0,25
Với lnx = 2
x = e
2
(thỏa đk) 0,25
Với lnx = 3
x = e
3
(thỏa đk)
Vậy phương trình có hai nghiệm: x = e2, x = e3. 0,25
3 Tính diện tích mặt cầu và thể tích khối cầu …..
Gọi O là tâm hình vuông ABCD, ta có OA = OB = OC = OD = a;
OS2 = SA2 - OA2 = 2a2 - a2 = a2 OS = a. Vậy tâm của mặt cầu ngoại
tiếp hình chóp S.ABCD là O, bán kính R = a.
0,50
Diện tích mặt cầu S = 4
R
2
= 4
a
2
. 0,25
Thể tích khối cầu V =
3 3
4 4
R a
3 3
0,25
Vb Phần dành cho học sinh học theo sách Toán 12 chuẩn 3,00
1 Viết phương trình tiếp tuyến …..
Tiếp tuyến
song song với đường thẳng 3x - 4y = 0 nên có hệ số góc
k = 3/4. Gọi (x
0
; y
0
) là tọa độ tiếp điểm, ta có k = 3/4 = y’(x
0
). 0,25
0
2 2
0
3 3
y ' , x 1 y '(x )
(x 1) (x 1)
.
y’(x
0
) = 3/4 (x
0
- 1)2 = 4 x
0
= -1 hoặc x
0
= 3.
0,25
Với x0 = -1, y0 = 5/2, ta có tiếp tuyến tại (-1; 5/2) là y =
3 5
(x 1)
4 2
. 0,25
Với x0 = 3, y0 = -1/2, ta có tiếp tuyến tại (3; -1/2) là y =
3 1
(x 3)
4 2
. 0,25
2 Giải phương trình:
2x x log2
6 2 5.10
.
Tập xác định:
฀
.
2x xlog 2
6 2 5.10 x
2x log2 2x x
6 2 5.10 6 2 5.2
0,25
2x x
2 5.2 6 0
2x = 2 hoặc 2x = 3. 0,25
Với 2
x
= 2
x = 1. 0,25
….. Hết …..
Ghi chú: Trong từng câu, học sinh có thể làm theo cách khác, giáo viên tùy theo mức độ để
cho điểm hợp lí.
Với 2
x
= 3
x = log
2
3. 0,25
3
Gọi O là tâm của hình vuông ABCD, ta có hình nón ngoại tiếp hình chóp
S.ABCD có bán kính đường tròn đáy R = OA = a; chiều cao = SO = a;
đường sinh SA =
a 2
.
0,50
Diện tích xung quanh của hình nón S
xq
= R.SA = a2
2
. 0,25
Thể tích của hình nón V =
2 2 3
1 1 1
R .SO a .a a
3 3 3
. 0,25