ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
Đề số 21
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN: (3 điểm)
Khoanh tròn vào chữ cái đứng trước câu trả lời đúng.
Câu1: Góc nội tiếp chắn nửa đường tròn có số đo bằng?
0 0 0 0
. 30 . 90 . 60 . 180
A B C D
Câu 2: Cho đường tròn tâm O bán kính bằng 3cm, khi đó độ dài đường tròn là?
. 6 ( ) . 9 ( ) . 8 ( ) . 3 ( )
A cm B cm C cm D cm
Câu 3: Tổng hai góc đối của một tứ giác nội tiếp bằng?
0 0 0 0
. 90 . 270 . 180 . 360
A B C D
Câu 4: Trên đường tròn bán kính R, độ dài l của một cung n0 được tính theo công thức
2 2
. . . .
Rn R n Rn R n
A l B l C l D l
Câu 5: Diện tích hình quạt tròn bán kính R, cung
0
n
được tính theo công thức:
A.
360
Rn
S
B.
2
180
R n
S
C.
2
360
R n
S
D.
180
Rn
S
Câu 6: Diện tích hình tròn bán kính R được tính theo công thức:
A. 2
S R
B.
2
S R
C.
3
S R
D.
S R
PHẦN II: TỰ LUẬN (7 điểm)
Câu 7: (2 điểm)
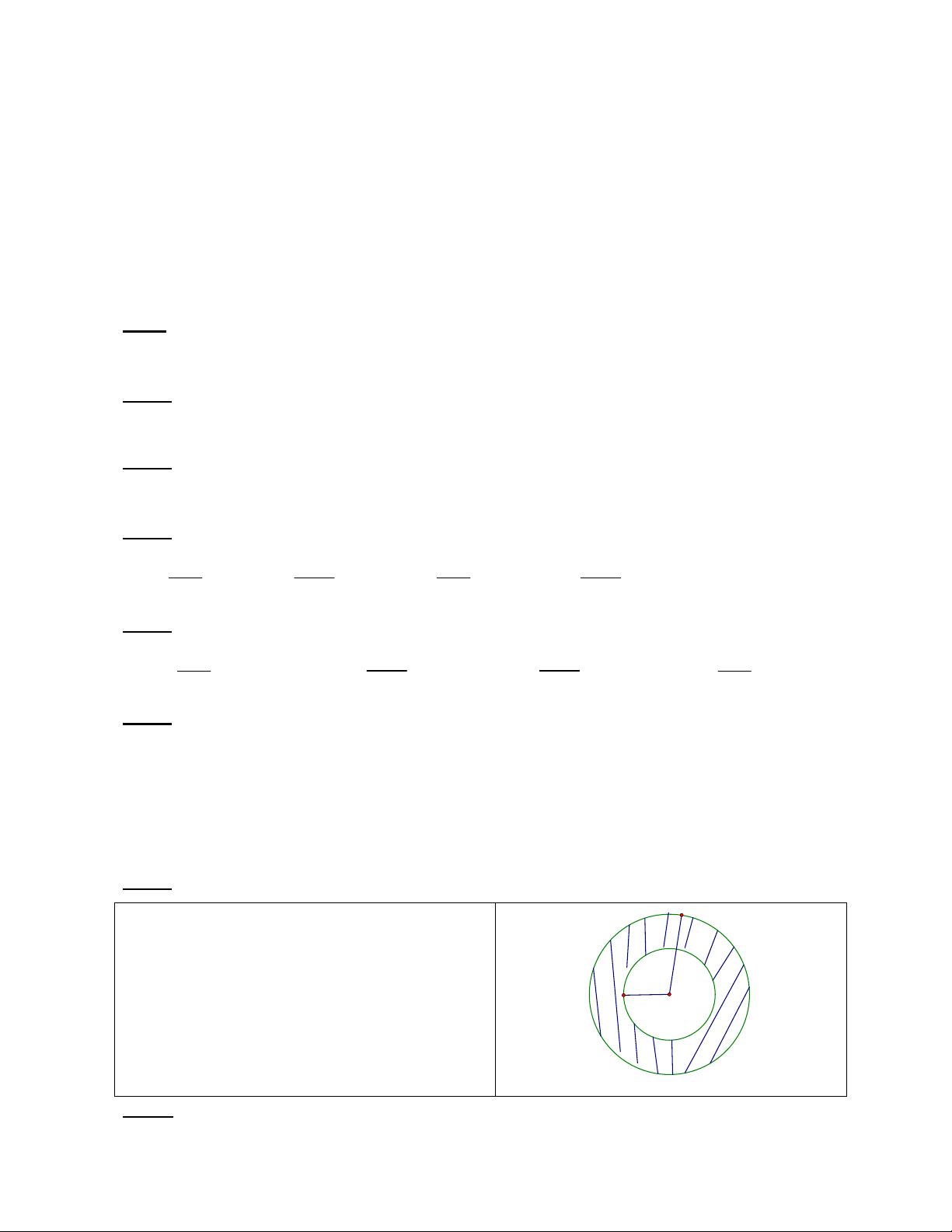
Trong hình vẽ, cho hai đường tròn đồng tâm O,
biết R = 3cm, r = 2cm. Tính diện tích miền
gạch sọc trong hình vẽ
R
r
Câu 8:(5 điểm) Cho tam giác ABC vuông tại A, điểm D nằm giữa A và B. Đường tròn đường
kính BD cắt BC tại E, đường thẳng CD cắt đường tròn tại điểm thứ hai là G.
Chứng minh rằng:
a) Tứ giác ADEC nội tiếp.
b) Tứ giác AGBC nội tiếp, xác định tâm và bán kính của đtròn ngoại tiếp tứ giác AGBC.
c) Ba đường thẳng AC, BG, DE đồng quy.
ĐÁP ÁN VÀ THANG ĐIỂM
Phần I: TNKQ ( 3 điểm ).
Câu 1 2 3 4 5 6
Đáp án B A C A C B
Thang điểm 0,5 0,5 0,5 0,5 0,5 0,5
Phần II: Tự luận ( 7 điểm).
Câu
Đáp án Điểm
Câu
7
(2đ)
-
gọi S, S1, S2 lần lượt là diện tích của miền gạch sọc, của hình tròn bán kính R
và hình tròn bán kính r
1,0
- ta có:
2 2
1 2
( )
S S S R r
0,5
Thay số
2 2 2
(3 2 ) 5 ( )
S cm
0,5
Câu
8
(5đ)
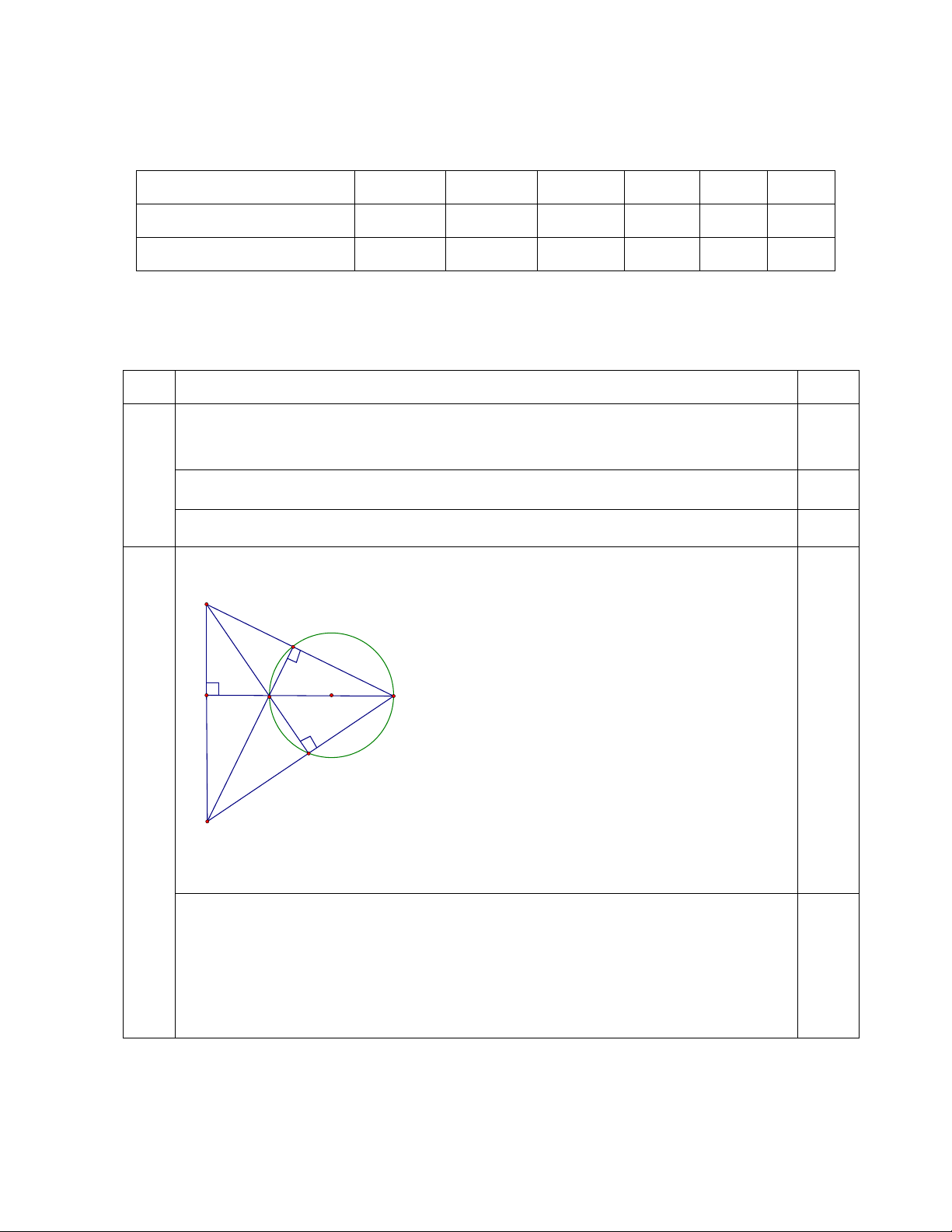
Vẽ hình chính xác, rõ ràng.
O
H
G
E
D
C
BA
1,0
a) ta có:
·
0
90
BED (góc nội tiếp chắn nửa đường tròn)
·
0
90
DEC (kề bù)
Xét tứ giác ADEC, ta có:
· ·
0 0 0
90 90 180
DEC DAC
Mà 2 góc này ở vị trí đối nhau nên tứ giác ADEC nội tiếp
1,5
b) ta có:
·
0
90
BGD (góc nội tiếp chắn nửa đtr)
·
0
90
BGC
xét tứ giác AGBC ta có:
·
·
0
90BAC BGC
2 điểm A, G cùng nhìn cạnh BC
dưới một góc vuông, nên A, G thuộc đường tròn có tâm là trung điểm của BC
và bán kính bằng BC/2
1,0
c) Tam giác CDB có CA, BG, DE là 3 đường cao nên chúng đồng quy. 1,5
ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
Đề số 22
Phần I: Trắc nghiệm khách quan: (4 điểm)
Hãy khoanh tròn vào chữ cái đứng trước câu trả lời đúng nhất:
1} Phương trình x – 3y = 2 cùng với phương trình nào trong các phương trình sau đây lập thành
một hệ phương trình vô nghiệm:
A. 2x – 6y = 4 B. 2x – 6y = 2 C. 2x + 3y = 1 D. x + 2y = 11
2) Cặp số ( 2 ; 1 ) là một nghiệm của phương trình nào sau đây:
A. x + y = 4 B. 2x + y = 5 C. 2x + y = 3 D. x + 2y = 3
3) Hệ phương trình :
4 5 3
3 5
x y
x y
có nghiệm là:
A. ( 2 ; 1 ) B. ( -2 ; -1 ) C. ( 2 ; -1 ) D. ( 3 ; 1 )
4) Hai đường thẳng y = ( k+1 ) x + 3 ; y = (3 – 2k) x + 1 song song khi :
A. k = 0 B. k =
2
3
C. k =
3
2
D. k =
4
3
5) Cặp số sau là 1 nghiệm của phương trình 3x – 2y = 5:
A. (1;-1) B.(5;-5) C.(1;1) D(-5;5).
6) Tập nghiệm của phương trình 2x – 0y = 5 được biểu diễn bởi đường thẳng
A. y = 2x – 5 B. y =
5
2
C. y = 5 – 2x D. x =
5
2
.
7) Hệ phương trình nào sau đây vô nghiệm ?
A.
x y 0
x y 0
ì
+ =
ï
ï
í
ï
- =
ï
î
B.
x y 0
x y 4
ì
- =
ï
ï
í
ï
+ =
ï
î
C.
x y 4
3x 2y 0
ì- =
ï
ï
í
ï
- =
ï
î
D.
x y 4
x y 0
ì- =
ï
ï
í
ï
- - =
ï
î
8) Hai hệ phương trình
3x 3y 3
kx 3y 3
;
y x 1
xy1
ì
ì + =
+ =
ï ï
ï ï
í í
ï ï - =
- + =
ï ï
îî
là tương đương khi k bằng:
A. 3 B. -3 C. 1 D. -1
Phần II: Tự luận: (6điểm)
Bài 1: (2điểm) Giải các hệ phương trình sau:
a)
2
2 3 9
x y
x y
b) 3 2 2 7
2 3 3 2 6
x y
x y
Bài 2: (3điểm) Giải bài toán bằng cách lập hệ phương trình: