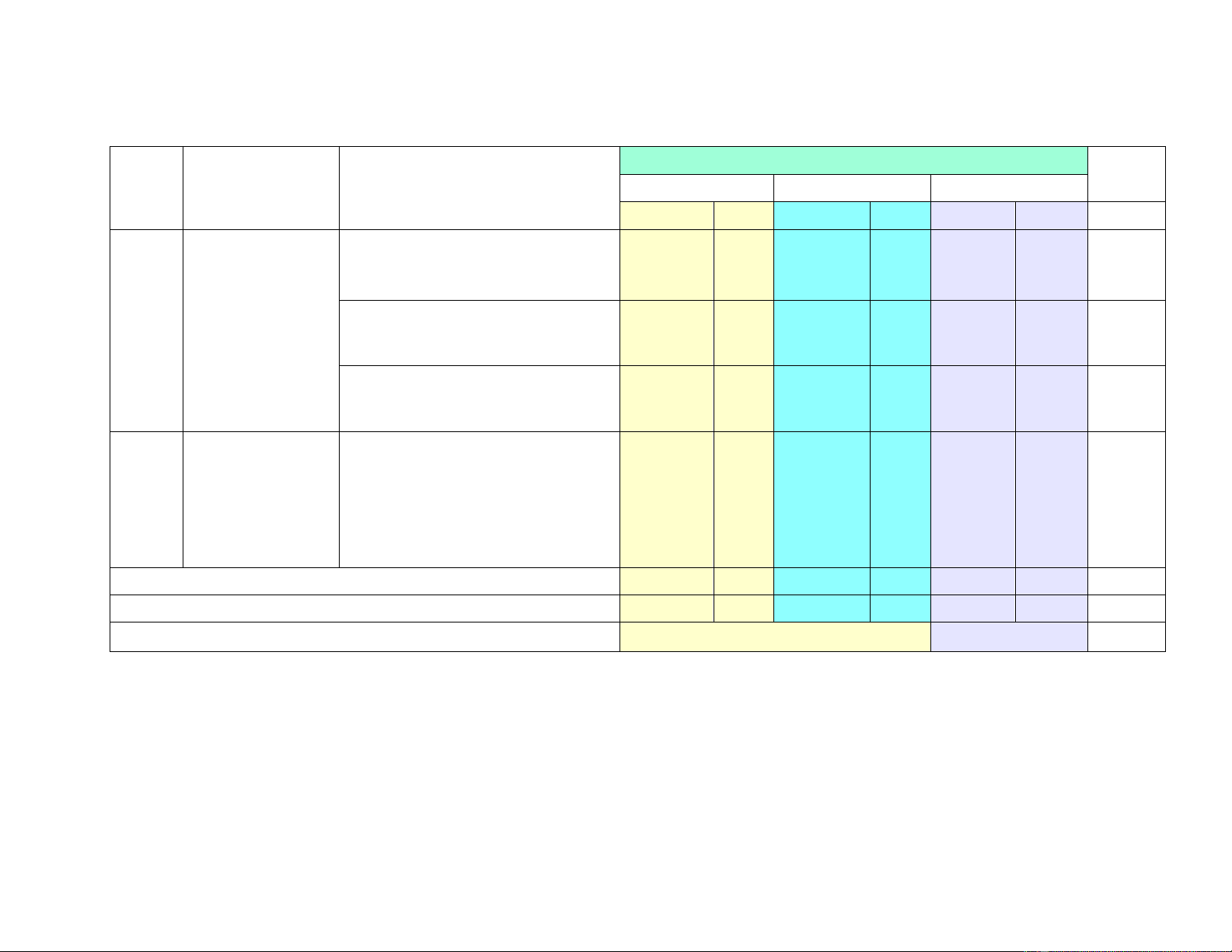
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ II_NĂM HỌC 2024-2025
MÔN: TOÁN 9
TT
Chủ đề
Nội dung/ Đơn vị kiến thức
Mức độ đánh giá
Tổng %
điểm
Nhận biết
Thông hiểu
Vận dụng
TL
TNKQ
TL
TNKQ
TL
1
Hàm số
y = ax
2
(a
≠
0 )
Phương trình
bậc hai
một ẩn
Hàm số
y = ax
2
(a
≠
0 )
và đồ
thị
1
0,5đ
1
1,0đ
Phương trình bậc hai một ẩn.
Định lí Viète.
1
1,0đ
3
2,0đ
Giải bài toán bằng cách lập
phương trình
1
1,0đ
2
Tần số và tần số
tương đối
Bảng tần số và biểu đồ tần số.
Bảng tần số tương đối và biểu
đồ tần số tương đối. Bảng tần
số, tần số tương đối ghép nhóm
và biểu đồ
1
0,5đ
2
1,0đ
Tổng
2
4
4
22
Tỉ lệ %
10
30
30
100%
Tỉ lệ chung
70%
30%
100%
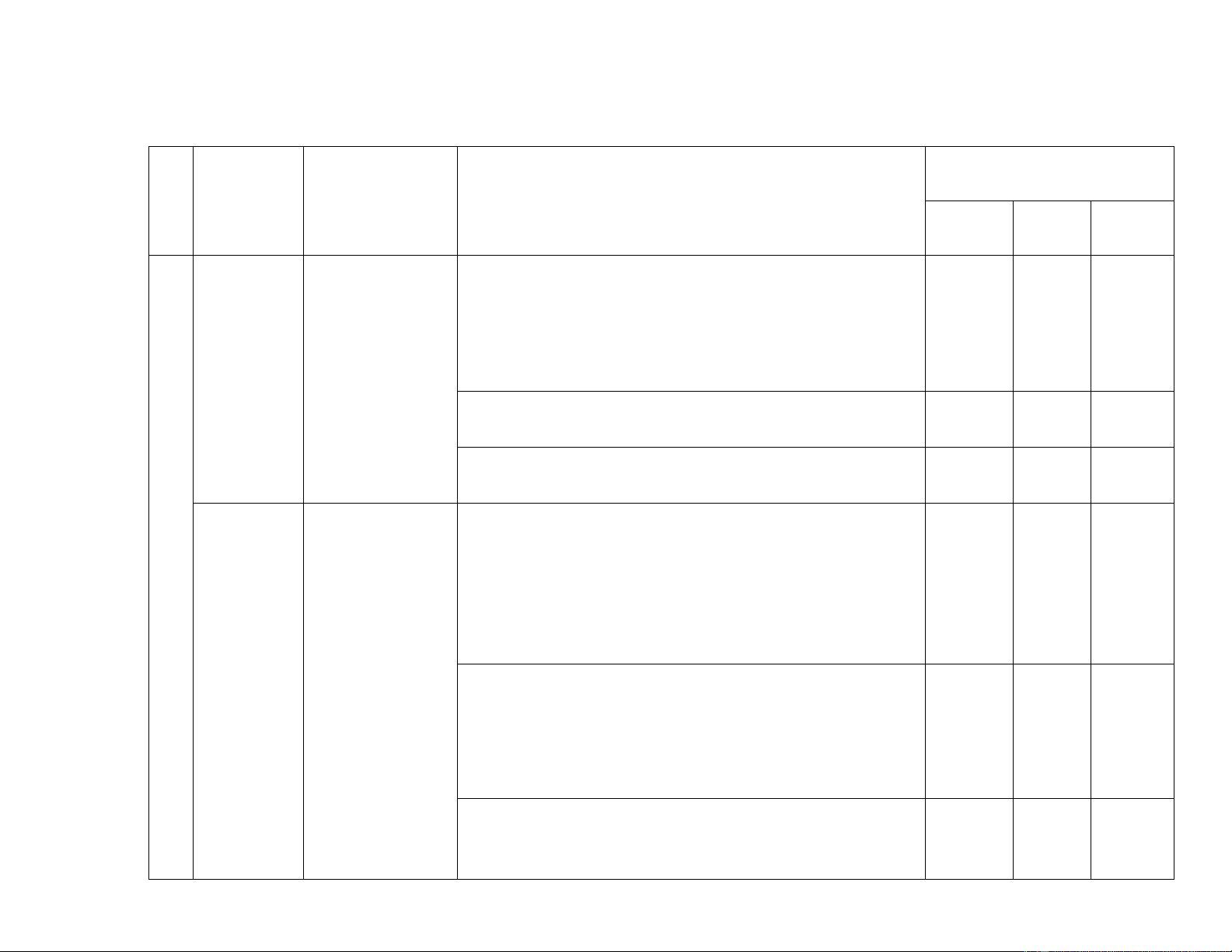
BẢN ĐẶC TẢ ĐỀ KIỂM TRA GIỮA HỌC KÌ II_NĂM HỌC 2024-2025
MÔN: TOÁN 9
TT
Chủ đề
Nội dung/ Đơn
vị kiến thức
Mc độ đánh giá
Số câu hỏi theo mc độ
nhận thc
Nhận
biêt
Thông
hiểu
Vận
dụng
1
Hàm số và
đồ thị
Hàm số y ax2
(a ≠ 0) và đồ thị
Nhận biết:
– Nhận biết được tính đối xứng (trục) và trục đối
xứng của đồ thị hàm số y ax2 (a ≠ 0).
– Xác định được giá trị của hàm số khi biết giá trị
của biến.
3TN
C1,2,3
1TL
B1a
Thông hiểu:
– Thiết lập được bảng giá trị của hàm số y ax2 (a ≠ 0).
1TL
B1b
Vận dụng:
– Vẽ được đồ thị của hàm số y = ax2 (a ≠ 0).
Phương
trình bậc
hai một
ẩn.
Phương trình
bậc hai một ẩn.
Định lí Viète.
Giải bài toán
bằng cách lập
phương trình
Nhận biết:
– Nhận biết được khái niệm phương trình bậc hai một ẩn.
– Xác định các hệ số a, b, c của phương trình bậc hai
một ẩn.
– Xác định được số nghiệm của phương trình khi biết
dấu của biệt thức/ biệt thức thu gọn.
6
C4,5,6,7
.8,9
Thông hiểu:
– Tính được nghiệm phương trình bậc hai một ẩn bằng
máy tính cầm tay.
– Giải được phương trình bậc hai một ẩn.
– Giải thích được định lí Viète.
1TL
B3a
Vận dụng:
– Giải được phương trình bậc hai một ẩn.
– Ứng dụng được định lí Viète vào tính nhẩm nghiệm của
2TL
B3b
B4
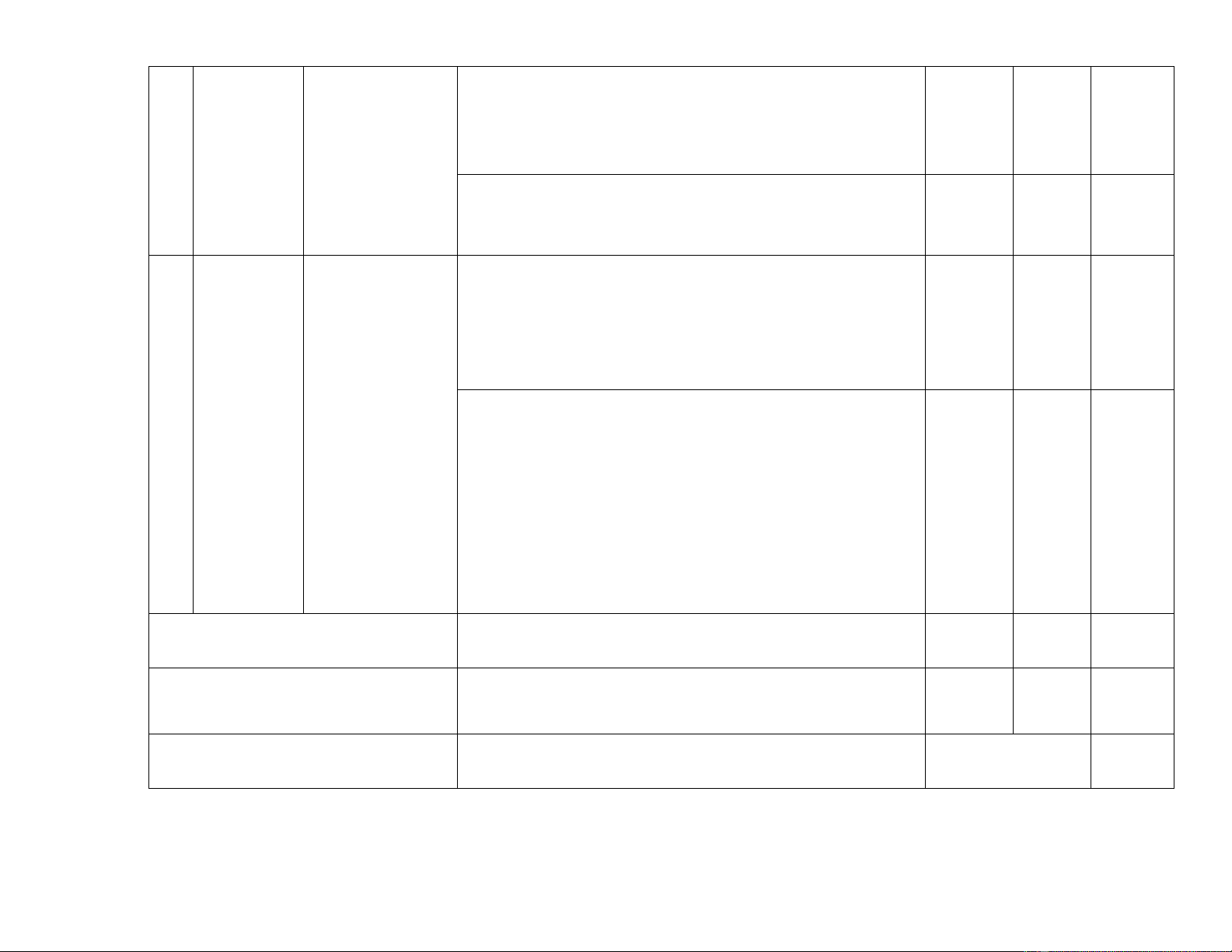
phương trình bậc hai, tìm hai số biết tổng và tích của
chúng, ...
– Vận dụng được phương trình bậc hai vào giải quyết bài
toán thực tiễn (đơn giản, quen thuộc).
Vận dụng cao:
– Vận dụng được phương trình bậc hai vào giải quyết bài
toán thực tiễn (phức hợp, không quen thuộc).
2TL
B5a,b
2
Tần số và
tần số
tương đối
Bảng tần số và
biểu đồ tần số.
Bảng tần số
tương đối và
biểu đồ tần số
tương đối. Bảng
tần số, tần số
tương đối ghép
nhóm và biểu đồ
Nhận biết:
– Nhận biết được mối liên hệ giữa thống kê với những
kiến thức của các môn học khác trong Chương trình
lớp 9 và trong thực tiễn.
3
C10,11,
12
1TL
2a
Thông hiểu:
– Giải thích được ý nghĩa và vai trò của tần số trong
thực tiễn.
– Giải thích được ý nghĩa và vai trò của tần số tương
đối trong thực tiễn.
– Thiết lập được bảng tần số, biểu đồ tần số (biểu diễn
các giá trị và tần số của chúng ở dạng biểu đồ cột hoặc
biểu đồ đoạn thẳng).
2TL
B2b,c
Tổng
14
(4đ)
4
(3đ)
4
(3đ)
Tỉ lệ %
40%
30%
30%
Tỉ lệ chung
70%
30%
UBND HUYỆN NÚI THÀNH
TRƯỜNG THCS NGUYỄN TRÃI
KIỂM TRA GIỮA KỲ II_ NĂM HỌC 2024-2025
Môn: Toán học – Lớp: 9
Thời gian: 90 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Lựa chọn 01 đáp án đúng nhất và ghi vào giấy làm bài.
Câu 1: Đồ thị của hàm số y = ax2 (a ≠ 0) luôn đi qua điểm nào sau đây?
A. (0; 1). B. (1; 0).
C. (0; 0). D. (1; 1).
Câu 2: Điểm đối xứng với điểm có tọa độ (–a; b) qua trục Oy là
A. (b; –a). B. (–b; a).
C. (a; –b). D. (a; b).
Câu 3: Hàm số y = ax2 (a≠ 0) có đồ thị nằm bên trên trục hoành khi
A.
a
>
0.
B.
a
<
0 .
C
. a
≤
0.
D.
a
=
0.
Câu 4: Phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆’ bằng
A. b’2 + ac. B. b’2 – ac.
C. b’2 + 4ac. D. b’2 – 4ac.
Câu 5: Tổng hai nghiệm của phương trình x2 – 5x + 2 = 0 là
A.
5.
B.
–5.
C
.
2
5
.
D.
−
2
5
.
Câu 6: Phương trình nào sau đây là phương trình bậc hai một ẩn ?
A. 3x2 + 2y = -1. B. 3x2 + 4x – 3 = 0.
C. 3x – 2y = 0 . D. 0x2 + 2x + 3 = 0.
Câu 7. Nếu hai số u, v có tổng là S và tích là P thì hai số u, v là nghiệm của phương trình.
A. x2 – Sx + P = 0. B. x2 + Sx + P = 0.
C. x2 – Sx – P = 0. D. x2 + Sx – P = 0.
Câu 8. Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ = b2 – 4ac > 0. Khi đó
phương trình có hai nghiệm là
A. x1 = x2 = b
2a. B. x1 = −b
2a ; x2 = b
2a.
C. x1 = −𝑏+√∆
2𝑎 ; x2 = −𝑏−√∆
2𝑎 . D. x1 = x2 = −b
2a.
Câu 9: Phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0), có a + b + c = 0. Khi đó, hai nghiệm của
phương trình là
A. x1 = –1; x2 = - c
a. B. x1= 1; x2 = c
a.
C. x1 = –1; x2 = 𝑐
𝑎. D. x1 = 1; x2 = - c
a
Câu 10: Tần số của một giá trị là
A. biểu đồ biểu diễn bảng tần số.
B. bảng thống kê cho biết tần số của các giá trị trong mẫu dữ liệu.
C. số giá trị của mẫu dữ liệu.
D. số lần xuất hiện giá trị đó trong mẫu dữ liệu.
ĐỀ CHÍNH THỨC
MÃ ĐỀ: A
Câu 11: Cho x1 là một trong các giá trị khác nhau của mẫu dữ liệu cỡ n = 20. Biết rằng tần
số của giá trị này là m1= 8. Khi đó tần số tương đối f1 của giá trị x1 là
A.
15%.
B.
20%.
C
. 40%.
D.
60%.
Câu 12: Số đo cung tương ứng của hình quạt biểu diễn tần số tương đối f3 = 20% là
A. 27°. B. 74°.
C. 36°. D. 72°.
II. PHẦN TỰ LUẬN (7 điểm)
Bài 1. (1,5 điểm) Cho hàm số y = ax2(a ≠ 0).
a) Tìm a đề đồ thị hàm số đi qua điểm A( 2; 2)
b) Vẽ đồ thị hàm số với a vừa tìm được ở câu a.
Bài 2. (1,5 điểm)
Bảng thống kê sau cho biết kết quả bài kiểm tra cuối học kì 1 môn toán của lớp 9A như sau:
Điểm số
7
8
9
10
Số học sinh
6
15
6
3
a) Hỏi lớp 9A đó có bao nhiêu học sinh.
b) Lập bảng tần số tương đối cho bảng thống kê trên.
c) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối thu được ở câu b.
Bài 3. (2,0 điểm)
a) Giải phương trình x2 + 7x – 8 = 0.
b) Tìm hai số u, v biết u + v = –8; uv = 12.
Bài 4. (1,0 điểm) Giải bài toán sau bằng cách lập phương trình:
Khoảng cách giữa hai bến sông A và B là 54 km. Một ca nô chạy xuôi dòng từ bến A
đến bến B rồi chạy ngược dòng từ bến B về bến A hết tất cả 7 giờ 30 phút. Tính vận tốc thực
của ca nô (tức là vận tốc của ca nô khi nước yên lặng), biết vận tốc dòng nước là 3 km/h.
Bài 5. (1,0 điểm)
Cho phương trình: x2 – (m – 2)x – 2m = 0 (1), x là ẩn, m là tham số.
a) Chứng minh phương trình (1) luôn có hai nghiệm với mọi giá trị của
b) Tìm m để phương trình có hai nghiệm x1, x2 sao cho biểu thức A = x12 + x22 đạt giá
trị nhỏ nhất.
..………………….HẾT……………………
.m