5 ĐỀ THI HỌC SINH GIỎI
MÔN TOÁN LỚP 7
NĂM 2017-2018 (CÓ ĐÁP ÁN)
1. Đề thi chọn học sinh giỏi cấp huyện môn Toán 7 năm 2017-2018
có đáp án - Phòng GD&ĐT Hậu Lộc
2. Đề thi chọn học sinh giỏi cấp huyện môn Toán 7 năm 2017-2018
có đáp án - Phòng GD&ĐT huyện Than Uyên
3. Đề thi chọn học sinh giỏi cấp huyện môn Toán 7 năm 2017-2018
có đáp án - Phòng GD&ĐT huyện Trực Ninh
4. Đề thi chọn học sinh giỏi cấp huyện môn Toán 7 năm 2017-2018
có đáp án - Phòng GD&ĐT huyện Vĩnh Bảo
5. Đề thi chọn học sinh giỏi cấp huyện môn Toán 7 năm 2017-2018
có đáp án - Phòng GD&ĐT Tam Dương
PHÒNG GD&ĐT
ĐỀ THI GIAO LƯU HỌC SINH GIỎI
MÔN: TOÁN 7
NĂM HỌC 2017 – 2018
Ngày thi: 26/3/2018
(Thời gian làm bài: 120 phút)
Bài 1. (4,0 điểm).
a) Tính: A =
2
13 8 19 23
1 . 0,5 .3 1 :1
15 15 60 24




b) So sánh:
20
16
và
100
2
Bài 2. (3,0 điểm).
a) Tìm
x
biết:
11
2 7 1
22
x
b) Tìm số tự nhiên n biết:
15
3 .3 4.3 13.3
nn
Bài 3. (4,5 điểm).
a) Cho dãy tỉ số bằng nhau:
d
dcba
c
dcba
b
dcba
a
dcba 2222
Tính giá trị biểu thức Q, biết Q =
cb
ad
ba
dc
ad
cb
dc
ba
b) Cho biểu thức
x y z t
Mx y z x y t y z t x z t
với x, y, z, t là các số
tự nhiên khác 0. Chứng minh
10 1025M
.
Bài 4. (6,5 điểm).
1) Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC, D là điểm thuộc
đoạn BM (D khác B và M). Kẻ các đường thẳng BH, CI lần lượt vuông góc với đường
thẳng AD tại H và I. Chứng minh rằng:
a)
BAM = ACM
và BH = AI.
b) Tam giác MHI vuông cân.
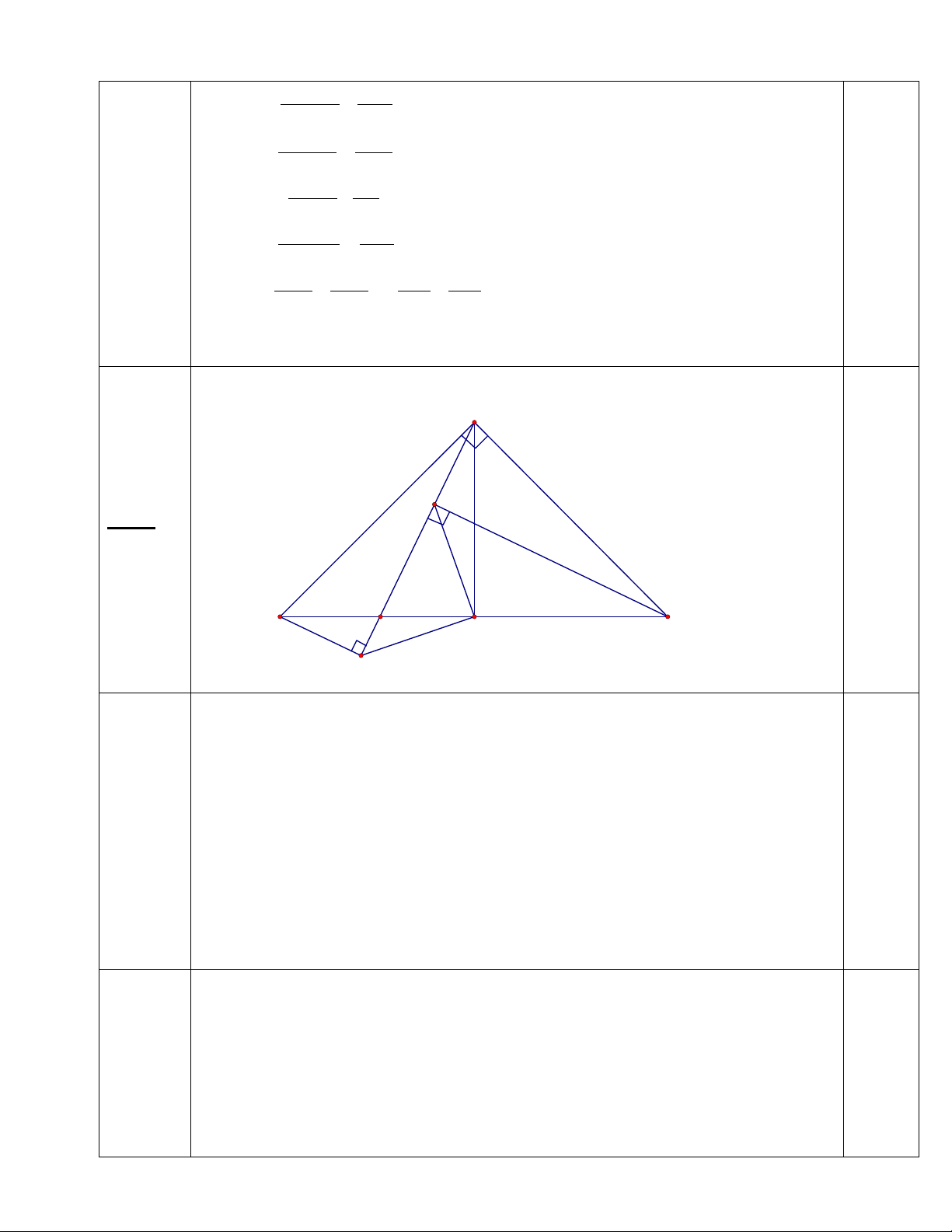
2) Cho tam giác ABC có góc  = 900. Kẻ AH vuông góc với BC (H thuộc BC). Tia
phân giác của góc HAC cắt cạnh BC ở điểm D và tia phân giác của góc HAB cắt cạnh
BC ở E. Chứng minh rằng AB + AC = BC + DE.
Bài 5. (2,0 điểm).
Cho x, y, z là 3 số thực tùy ý thỏa mãn x + y + z = 0 và
11x
,
11y
,
11z
. Chứng minh rằng đa thức
2 4 6
x y z
có giá trị không lớn hơn 2.
-----Hết-----
Họ và tên thí sinh: …………………………….. Số báo danh: ..............
Thí sinh không được sử dụng máy tính cầm tay khi làm bài.
ĐỀ HSG TOÁN 7
HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
Bài 1.
4,0 đ
a) 2,0 đ
+ Biến đổi:
7 47 47
:
5 60 24
A
=
72
55
= 1
1,0
0,50
0,50
b) 2,0 đ
+ Biến đổi:
20 4.20 80
16 2 2
+ Có
80 100
22
vì (1 < 2 ; 80 < 100)
Vậy
20 100
16 2
0,5
1,0
0,5
Bài 2.
3,0 đ
a) 2,0 đ
+ Ta có
11
2 7 1
22
x
=>
2 7 1x
=>
2 7 1x
hoặc
2 7 1x
=>
4x
hoặc
3x
Vậy
4x
hoặc
3x
.
0,5
0,5
0,5
0,5
b) 1,0 đ
+ Biến đổi được
15
3 .(3 4) 13.3
n
=>
6
33
n
=> n = 6
KL: Vậy n = 6
0,25
0,25
0,25
0,25
Bài 3.
4,5 đ
a)
(2,5 đ)
+ Biến đổi:
d
dcba
c
dcba
b
dcba
a
dcba 2222
2 2 2 2
1111
a b c d a b c d a b c d a b c d
a b c d
a b c d a b c d a b c d a b c d
a b c d

+ Nếu a + b + c + d
0 thì a = b = c = d => Q = 1 + 1 +1 +1 = 4
+ Nếu a + b + c + d = 0
thì a + b = - (c + d); b + c = - (d + a); c + d = - (a + b); d + a = - (b + c)
=> Q = (-1) + (-1) + (-1) +(-1) = - 4
+ KL : Vậy Q = 4 khi a + b + c + d
0
Q = - 4 khi a + b + c + d = 0
0,5
0,25
0,25
1,0
0,25
0,25
b)
(2,0 đ)
+ Ta có:
xx
x y z x y
yy
x y t x y
zz
y z t z t
tt
x z t z t
M <
)
tz
t
tz
z
()
yx
y
yx
x
(
=> M < 2
+ Có M10 < 210 (Vì M > 0) mà 210 = 1024 < 1025
Vậy M10 < 1025
0,1
0,25
0,5
0,25
Bài 4.
0,25
1.a/
2,75 đ
* Chứng minh:
BAM ACM
+ Chứng minh được: ABM = ACM (c-c-c)
+ Lập luận được:
0
45BAM CAM
+ Tính ra được
0
45ACM
=>
BAM ACM
* Chứng minh: BH = AI.
+ Chỉ ra:
BAH ACI
(cùng phụ
DAC
)
+ Chứng minh được AIC = BHA (Cạnh huyền – góc nhọn)
=> BH = AI (2 cạnh tương ứng)
0,5
0,25
0,25
0,25
0,5
0,75
0,25
1.b/
2,0 đ
b) Tam giác MHI vuông cân.
+ Chứng minh được
AM BC
+ Chứng minh được AM = MC
+ Chứng minh được
HAM ICM
+ Chứng minh được HAM = ICM (c-g-c)
=> HM = MI (*)
+ Do HAM = ICM =>
HMA IMC
=>
HMB IMA
(do
0,25
0,25
0,25
0,25
0,25
0,25
I
H
A
M
B C
D