Bài giảng biến đổi năng lượng điện cơ chương 2

Chia sẻ: Nguyễn Phước Lộc | Ngày: | Loại File: PDF | Số trang:18

Thêm vào BST

Báo xấu

131
lượt xem 14
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'bài giảng biến đổi năng lượng điện cơ chương 2', kỹ thuật - công nghệ, năng lượng phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng biến đổi năng lượng điện cơ chương 2

408001 Bi n ñ i năng lư ng ñi n cơ TS. Nguy n Quang Nam HK2, 2009 – 2010 http://www4.hcmut.edu.vn/~nqnam/lecture.php nqnam@hcmut.edu.vn Bài gi ng 2 1 Gi i thi u Lý thuy t ñi n t : n n t ng gi i thích s ho t ñ ng c a t t c các h th ng ñi n và ñi n t . T n t i các h th ng v i t trư ng và ñi n trư ng, bài gi ng ch ñ c p ñ n các h th ng ng d ng t trư ng. D ng tích phân c a các phương trình Maxwell ∫ ∫J H • dl = • n da ð nh lu t Ampere f C S ∂B ∫ E • dl = − ∫ • n da ð nh lu t Faraday ∂t C S ∫ J • n da = 0 Nguyên t c b o toàn ñi n tích f S ∫ B • n da = 0 ð nh lu t Gauss S Bài gi ng 2 2
M ch t tĩnh Trong các m ch t tĩnh không có các ph n t chuy n ñ ng. Xét m ch t hình xuy n: N vòng dây qu n ñ u. r0 và r1 các bán kính trong và ngoài. Xét ñư ng s c tương ng v i bán kính trung bình r = (r0 + r1) / 2, gi s cư ng ñ t trư ng Hc là ñ u bên trong lõi. Theo ñ nh lu t Ampere, Hc(2πr) = Ni. Hay, H c l c = Ni v i lc = 2πr là chi u dài trung bình c a lõi. Gi thi t B là hàm tuy n tính theo H trong lõi, t c m c a lõi s là (Wb )/m 2 Ni Bc = µH c = µ lc Bài gi ng 2 3 M ch t tĩnh (tt) T thông cho b i µNi Ni φ c = Bc Ac = Ac = Wb l c µAc lc v i µ là ñ th m t c a v t li u lõi, Ac là ti t di n c a lõi. ð nh nghĩa Ni là s c t ñ ng (mmf), t tr có th ñư c tính b i Ni mmf l = = c = R (Av/Wb) φc flux µAc P = 1/R ñư c g i là t d n. T ñó, t thông móc vòng ñư c ñ nh nghĩa là λ = Nφc = PN2i. Theo ñ nh nghĩa, t c m L c a m t cu n dây cho b i λ N2 L = = PN = 2 R i Bài gi ng 2 4
M ch t tĩnh (tt) Có s tương ñ ng gi a m ch ñi n và m ch t S c t ñ ng ⇔ ði n áp T thông ⇔ Dòng ñi n T tr ⇔ ði n tr T d n ⇔ ði n d n Xét lõi xuy n có khe h (không có t t n): T n t i cư ng ñ t trư ng H trong c khe h l n lõi thép. lg – chi u dài khe h , lc – chi u dài trung bình c a lõi thép. Áp d ng ñ nh lu t Ampere d c ñư ng s c c Bg Bc Ni = H g l g + H c lc = lg + lc µ0 µ r µ0 v i µ0 = 4π x 10−7 H/m là ñ th m t c a không khí, và µr ñ th m t tương ñ i c a v t li u lõi. Bài gi ng 2 5 M ch t tĩnh (tt) Áp d ng ñ nh lu t Gauss cho m t kín s bao ph m t c c t , BgAg = BcAc. Không xét t t n, Ag = Ac. Do ñó, Bg = Bc. Chia s c t ñ ng cho t thông ñ xác ñ nh t tr tương ñương lg lc Ni = + = R g + Rc φ µ 0 Ag µAc V i Rg và Rc tương ng là t tr c a khe h và lõi t . Trong m ch t tương ñương, các t tr này n i ti p nhau. Gi s có “t t n”, t c là không ph i toàn b t thông b gi i h n b i di n tích gi a hai m t lõi t . Trong trư ng h p này, Ag > Ac, nghĩa là, di n tích khe h hi u d ng tăng lên. Có th xác ñ nh b ng th c nghi m, Ac = ab, Ag = (a + l g )(b + l g ) Bài gi ng 2 6
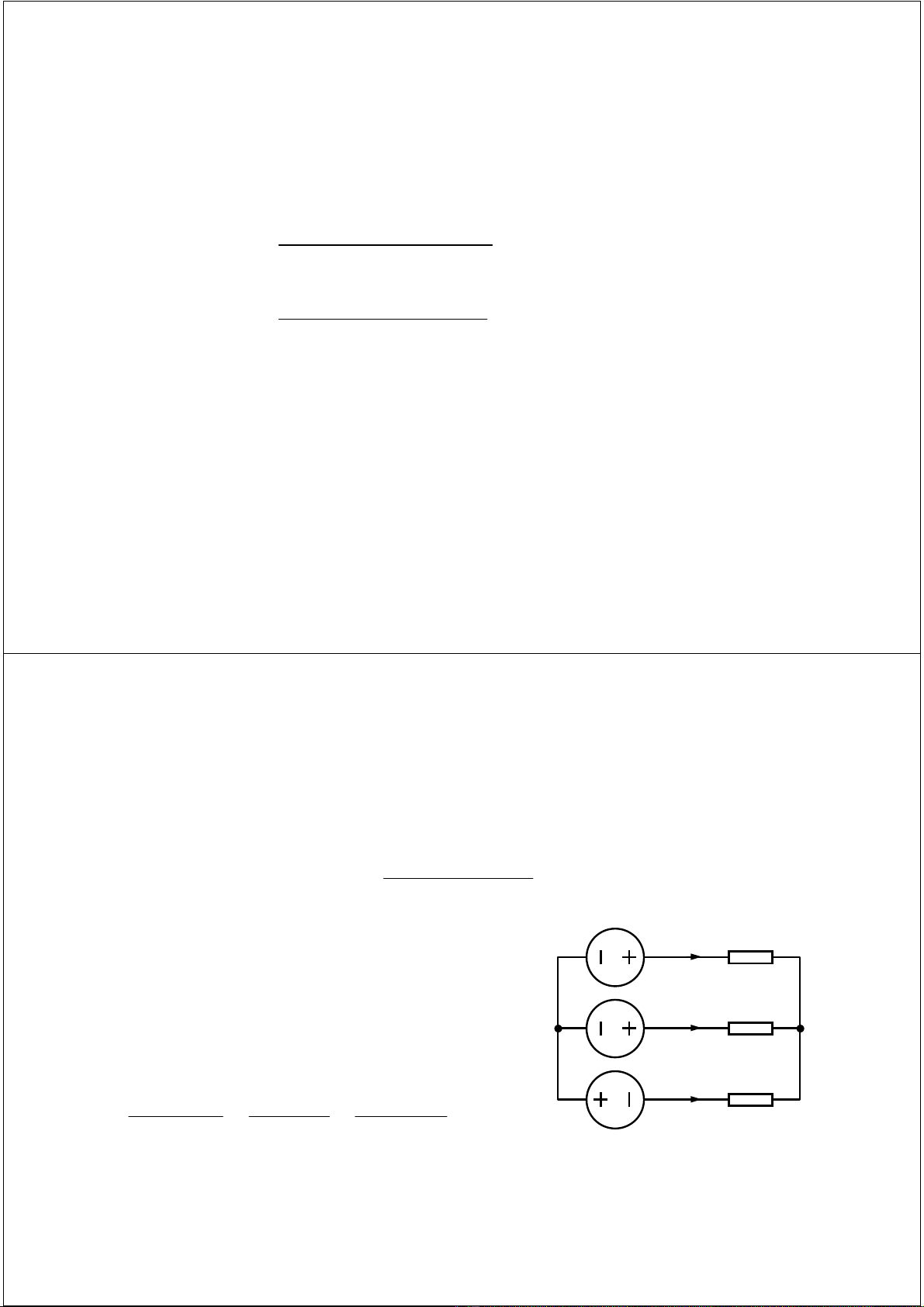
Ví d t i l p Vd. 3.1: Tìm s c t ñ ng c n thi t ñ t o ra m t t thông cho trư c. Chi u dài khe h và lõi t ñã bi t. 0,06 Rc = = 47,7 × 103 Av/Wb ( )( )( ) 10 4π × 10 10−7 −4 4 0,001 Rg = = 7,23 ×106 Av/Wb ( )( ) 4π × 10 1,1× 10 −7 −4 φ = Bg Ag = (0,5)(1,1×10 − 4 ) = 5,5 ×10 −4 Wb Do ñó, Ni = (Rc + R g )φ = (47,7 + 7230)×103 × 5,5 ×10−5 = 400 Av Bài gi ng 2 7 Ví d t i l p (tt) Ex. 3.2: Tìm t thông xuyên qua cu n dây. T t c khe h có cùng chi u dài và ti t di n. T th m c a lõi thép là vô cùng l n và b qua t t n. (0,1×10 ) = 1,989 ×10 −2 R1 = R2 = R3 =R = 6 (4π ×10 )(4 ×10 ) At/Wb −7 −4 2500 Trong m ch tương ñương th hi n chi u R dương c a φ1, φ2, và φ3. T ng ñ i s c a φ1 500 các t thông nút a ph i b ng 0. R b a φ2 G i s c t ñ ng gi a a và b là F, khi ñó 1500 R 2500 − F 500 − F F + 1500 + − =0 φ3 R R R Do ñó, F = 500, φ1 = 10 −3 Wb, φ 2 = 0, φ3 = −10 −3 Wb Bài gi ng 2 8
H cm H c m: tham s liên quan ñ n ñi n áp c m ng trong 1 cu n dây v i dòng ñi n bi n thiên theo th i gian trong 1 cu n khác. Xét 2 cu n dây qu n trên cùng m ch t , cu n 1 ñư c kích thích còn cu n 2 h m ch. T thông t ng c a cu n 1 là φ11 = φl1 + φ 21 v i φl1 (g i là t thông t n) ch móc vòng v i cu n 1; còn φ21 là t thông tương h móc vòng v i c hai cu n dây, cũng là t thông trong cu n 2 do dòng ñi n trong cu n 1 t o ra. Th t c a các ch s là quan tr ng. Vì cu n 2 h m ch, t thông móc vòng v i nó là λ2 = N 2φ 21 Bài gi ng 2 9 H c m (tt) λ2 = N 2φ21 = M 21i1 φ21 t l tuy n tính v i i1, do ñó ði n áp c m ng v2 (do s thay ñ i c a t thông móc vòng) cho b i dλ2 di v2 = = M 21 1 dt dt M21 ñư c g i là h c m gi a các cu n dây. Tương t , có th xác ñ nh ñi n áp c m ng v1 trong cu n 1 như sau. φ11 t l v i i1, do ñó λ1 = N1φ11 = L1i1, khi ñó dλ1 di v1 = = L1 1 dt dt v i L1 là t c m c a cu n 1, như ñã bi t. Bài gi ng 2 10
H c m (tt) Bây gi xét trư ng h p cu n 1 h m ch và cu n 2 ñư c kích thích. Có th dùng cùng quy trình ñ tính các ñi n áp c m ng. dλ1 di φ22 = φl 2 + φ12 v1 = = M 12 2 λ1 = N1φ12 = M 12i2 dt dt dλ2 di λ2 = N 2φ22 = L2i2 v2 = = L2 2 dt dt v i L2 là t c m c a cu n 2, như ñã bi t. Xét v m t năng lư ng, có th ch ng minh r ng M21 = M12 = M. Sau cùng, xét trư ng h p c hai cu n dây cùng ñư c kích thích. φ1 = φl1 + φ 21 + φ12 = φ11 + φ12 φ 2 = φ 21 + φl 2 + φ12 = φ 21 + φ 22 Bài gi ng 2 11 H c m (tt) Chý ý r ng M21 = M12 = M λ1 = N1φ11 + N1φ12 = L1i1 + Mi2 λ2 = N 2φ 21 + N 2φ 22 = Mi1 + L2 i2 B ng cách l y ñ o hàm, có th tính ñư c các ñi n áp c m ng di1 di di1 di v1 = L1 +M 2 v2 = M + L2 2 dt dt dt dt M k= H s ghép gi a hai cu n dây ñư c ñ nh nghĩa là L1 L2 Có th ch ng minh 0 ≤ k ≤ 1, hay, 0 ≤ M ≤ L1 L2 H u h t máy bi n áp lõi không khí ñư c ghép y u (k < 0,5), còn máy bi n áp lõi thép ñư c ghép m nh (k > 0,5, có th ti n ñ n 1). Bài gi ng 2 12
Ví d t i l p Vd. 3.4: Cho t tr c a 3 khe h trong m ch t . V m ch tương ñương và tính các t thông móc vòng và ñi n c m. N1i1 = R3 (φ1 − φ 2 ) + R1φ1 N 2 i2 = R 2φ 2 − R 3 (φ1 − φ 2 ) φ1 100i1 = (5φ1 − 2φ 2 ) × 10 6 100i2 = (− 2φ1 + 4φ 2 ) × 10 6 N1i1 Gi i các phương trình này theo φ1 và φ2 R1 φ2 = (12,5i1 + 31,25i2 )×10 −6 R3 φ1 = (25i1 + 12,5i2 )×10 −6 λ1 = N1φ1 = (25i1 + 12,5i2 )×10 −4 R2 T N2i2 λ2 = N 2φ2 = (12,5i1 + 31,25i2 )×10 −4 φ2 −4 L1 = 25 ×10 H = 2,5 mH Có th th y M = 12,5 × 10 −4 H = 1,25 mH L2 = 31,25 ×10 −4 H = 3,125 mH Bài gi ng 2 13 ðánh d u c c tính (quy ư c d u ch m) ð nh lu t Lenz: ñi n áp c m ng theo chi u sao cho dòng ñi n ñư c sinh ra s t o ra t thông ch ng l i t thông gây c m ng ñi n áp. D u c a các ñi n áp c m ng ñư c theo dõi nh quy ư c ñánh d u ch m. M t dòng ñi n i ñi vào c c có (không có) d u ch m 1 dây qu n s c m ng 1 ñi n áp Mdi/dt v i c c tính dương ñ u có (không có) d u ch m c a cu n dây kia. Hai lo i bài toán: (1) cho bi t c u hình cu n dây, xác ñ nh các d u ch m. (2) cho bi t các d u ch m c c tính, vi t các phương trình m ch. Bài gi ng 2 14
Xác ñ nh c c tính Các bư c xác ñ nh: Ch n tùy ý 1 c c c a 1 cu n dây và gán d u ch m. Gi s 1 dòng ñi n ch y vào ñ u có d u ch m và xác ñ nh t thông trong lõi. Ch n m t c c b t kỳ c a cu n th hai và gán 1 dòng ñi n dương cho nó. Xác ñ nh chi u t thông do dòng ñi n này. So sánh chi u c a các t thông. N u c hai c ng tác d ng, d u ch m ñư c ñ t c c có dòng ñi n ñi vào c a cu n th hai. N u các t thông ngư c chi u, d u ch m ñư c ñ t c c có dòng ñi n ñi ra kh i cu n th hai. Bài gi ng 2 15 Cách xác ñ nh c c tính th c t V i các máy bi n áp, không có cách nào ñ bi t các cu n dây ñư c qu n ra sao, do ñó ngư i ta s d ng phương pháp th c t sau. Dùng 1 ngu n DC ñ kích thích m t cu n dây, xem hình bên. + ðánh d u ch m vào c c n i v i _ c c dương c a ngu n DC. ðóng công t c: Kim vôn k nhích theo chi u dương => d u ch m cho cu n dây kia n m c c n i v i c c dương c a vôn k . Kim vôn k nhích theo chi u âm => d u ch m n m c c n i v i c c âm c a vôn k . Bài gi ng 2 16
Vi t phương trình cho các cu n dây có h c m Cho hai cu n dây có h c m ñã ñánh d u c c tính, vi t phương trình. Ch n chi u b t kỳ cho các dòng ñi n. Quy t c: Dòng ñi n tham chi u ñi vào c c có (không có) d u ch m, ñi n áp c m ng trong cu n kia là dương (âm) ñ u có (không có) d u ch m. Dòng ñi n tham chi u r i kh i c c có (không có) d u ch m, ñi n áp c m ng t i c c có (không có) d u ch m c a cu n kia là âm. di1 di2 R1 R2 v1 = i1 R1 + L1 +M M dt dt i1 i2 di2 di1 v2 v1 v 2 = i 2 R 2 + L2 +M dt dt Bài gi ng 2 17 Ví d t i l p Vd 3.6: Vi t các phương trình m ch vòng cho m ch có h c m. Gi thi t ñi n áp ban ñ u trên t b ng 0 L2 R1 i1 v1 = i1 R1 + (i1 − i2 )R2 C R2 v1 M i2 + L1 (i1 − i2 ) − M 2 di d L1 dt dt (i1 – i2) di i2 dt + L2 2 − M (i1 − i2 ) + L1 (i2 − i1 ) 1t d d C ∫0 0= dt dt dt di + M 2 + (i2 − i1 )R2 dt Bài gi ng 2 18
Máy bi n áp – Gi i thi u Truy n t i ñi n năng t m t m ch sang m t m ch khác thông qua t trư ng. ng dung: c lĩnh v c năng lư ng l n truy n thông. Trong truy n t i, phân ph i, và s d ng ñi n năng: tăng hay gi m ñi n áp t n s c ñ nh (50/60 Hz), công su t hàng trăm W ñ n hàng trăm MW. Trong truy n thông, máy bi n áp có th ñư c dùng ñ ph i h p tr n kháng, cách ly DC, và thay ñ i c p ñi n áp công su t vài W trên m t d i t n s r t r ng. Môn h c này ch xem xét các máy bi n áp công su t. Bài gi ng 2 19 Máy bi n áp lý tư ng Xét m t m ch t có qu n 2 cu n dây như φ i1 i2 hình v . B qua các t n hao, ñi n dung ký + + v1 N1 N2 v2 sinh, và t thông rò. – – ð th m t vô cùng l n hay t tr b ng 0. v1 (t ) N1 dφ dφ v 2 (t ) = N 2 v1 (t ) = N 1 = =a ⇒ v 2 (t ) N 2 dt dt a ñư c g i là t s vòng dây. S c t ñ ng t ng cho b i mmf = N1i1 + N 2 i2 = Rφ = 0 i1 (t ) N 1 =− 2 =− ⇒ i2 (t ) N1 a Bài gi ng 2 20
Máy bi n áp lý tư ng (tt) i1 i2 v1 N1 i1 N Ideal 1 = =a =− 2 =− + + v2 N 2 i2 N1 a v1 v2 v1 (t )i1 (t ) + v2 (t )i2 (t ) = 0 – – N1:N2 i1 i2 v1 N1 i1 N 2 1 Ideal = =a = = + + v2 N 2 i2 N1 a v1 v2 v1 (t )i1 (t ) = v2 (t )i2 (t ) – – N1:N2 Có th th y r ng, v i m t máy bi n áp lý tư ng L2 i1 v 1 k =1 =− =− 2 =− L1 N 2 = L2 N 12 2 ⇒ i2 v1 a L1 Bài gi ng 2 21 Tính ch t thay ñ i tr kháng c a MBA lý tư ng Xét 1 MBA lý tư ng v i t i ñi n tr n i vào dây qu n 2 v2 = RL Theo ñ nh lu t Ohm i1 i2 i2 Ideal + + Thay v 2 = v1 a và i2 = ai1 RL v1 v2 2 N  v1 – – = a 2 RL =  2  RL N  N1:N2 i1  1 Có th d dàng m r ng k t qu trên cho các h th ng có t i ph c. Có th ch ng minh r ng 2 2 V1  N 2  V2  N 2  = =  ZL = a2ZL  I1  N1  I 2  N1      Bài gi ng 2 22
Ph i h p tr kháng Tính ch t thay ñ i tr kháng có th ñư c dùng ñ c c ñ i hóa vi c truy n công su t gi a các dây qu n, hay ph i h p tr kháng. M t MBA lý tư ng ñư c ñ t gi a ngu n công su t (tr kháng Zo) và t i (tr kháng ZL). T s vòng dây ñư c ch n sao cho Z o ≈ (N1 N 2 ) Z L 2 Vd. 3.7: Hai MBA lý tư ng (m i máy có t s 2:1) và m t ñi n tr R ñư c dùng ñ c c ñ i hóa vi c truy n công su t. Tìm R. ði n tr t i 4 Ω k t h p v i R ñư c quy ñ i v ngõ vào thành (R + 4(2)2)(2)2. ð có công su t truy n c c ñ i, R = 13,5 Ω 10 + 4 R = 64 ⇒ Bài gi ng 2 23 Máy bi n áp công su t Hai dây qu n trên m t lõi t , ñ gi m thi u t thông rò. Dây qu n “Sơ c p” (N1 vòng) n i vào ngu n ñi n, dây qu n “th c p” (N2 vòng) n i vào m ch t i. Gi thi t máy bi n áp là lý tư ng: không có t thông rò, b qua ñi n tr dây qu n, m ch t có ñ th m t vô cùng l n, và không t n hao. G i v1(t) = Vm1cosωt là ñi n áp ñ t vào dây qu n sơ c p, có th ch ng minh ñư c Vm1 = 2πfN 1φ max hay V1 = 4,44 fN1φmax Bài gi ng 2 24
M t s hình nh Công su t nh 3 pha nh ði u khi n Lo i khô 110 kV, ngâm d u 10 kV, ngâm d u 500 kV, ngâm d u Bài gi ng 2 25 Ví d t i l p Vd. 3.8: Cho bi t N1, N2, ti t di n lõi, chi u dài trung bình lõi, ñư ng cong B-H, và ñi n áp ñ t vào. Tìm t c m c c ñ i, và dòng ñi n t hóa c n thi t. V1 = 4,44 fN1φmax V1 = 230 V, f = 60 Hz, N1 = 200 vi 230 φmax = = 4,32 × 10 −3 Wb V y, 4,44 × 60 × 200 4,32 ×10 −3 Bm = = 0,864 Wb/m 2 Do ñó, 0,005 C n có H m = 0,864 × 300 = 259 A/m , giá tr ñ nh c a dòng ñi n t hóa là (259)(0,5)/200 = 0,6475 A. V y, Irms = 0,46 A là dòng ñi n t hóa phía sơ c p. Bài gi ng 2 26
M ch tương ñương c a MBA v i m ch t tuy n tính Xét m t MBA v i t thông rò và ñi n tr dây qu n. M ch tương ñương rút tr c ti p t mô hình v t lý là ñơn gi n nhưng không có ích l m. Các phương trình phía th c p ñư c nhân v i a (= N1/N2) và i2 ñư c thay th b i i2/a, ñ rút ra m t m ch tương ñương có ích hơn. 2 L1 – aM a2R2 a L2 – aM R1 i1 i2 + + + + i1 i2/a av2 a2RL RL v1 v2 v1 aM – – – – N1:N2 L1 – aM ñư c g i là ñi n kháng t n c a dây qu n 1, a2L2 – aM ñư c g i là ñi n kháng t n “quy ñ i” c a dây qu n 2. aM là ñi n kháng t hóa, và dòng ñi n ñi cùng v i nó ñư c g i là dòng ñi n t hóa. Bài gi ng 2 27 M ch tương ñương c a MBA v i m ch t tuy n tính (tt) T n t i t n hao công su t trong lõi t do t tr và dòng xoáy. Các t n hao này r t khó tính toán b ng gi i tích. T ng các t n hao này bi u di n t n hao t ng trong m ch t c a máy bi n áp, và ch ph thu c vào giá tr Bm. Chúng ñư c g i là t n hao (lõi) thép. M t ñi n tr có th ñư c m c song song v i ñi n kháng t hóa aM ñ k ñ n các t n hao này. 2 L1 – aM a2R2 a L2 – aM i1 R1 i2 Ideal + + + RL v1 av2 v2 Rc1 (aM)1 – – – N1:N2 T i th c RL và ñi n áp/dòng ñi n ñi cùng v i nó có th có ñư c b ng cách quy ñ i ngư c v phía th c p, qua m t MBA lý tư ng. Bài gi ng 2 28
Máy bi n áp v n hành xác l p hình sin Khi v n hành xác l p, các tr kháng và vectơ pha có th ñư c dùng trong m ch tương ñương. ja2xl2 jxl1 a2R2 R1 I2 Ideal + + + I1 I2 a ZL Rc1 jXm1 V1 aV2 V2 – – – N1:N2 vi ω (L1 − aM ) = xl1 = ði n kháng t n c a dây qu n 1 ω (aM ) = X m1 = ði n kháng t hóa quy ñ i v dây qu n 1 ω ( L2 − M a ) = x l 2 = ði n kháng t n c a dây qu n 2 ω (a 2 L2 − aM ) = a 2 xl 2 = ði n kháng t n c a d/qu n 2 quy ñ i v d/qu n 1 Bài gi ng 2 29 Máy bi n áp v n hành xác l p hình sin (tt) T t c các ñ i lư ng có th ñư c quy ñ i v dây qu n 1 ja2xl2 jxl1 a2R2 R1 + + I1 I2 a a2ZL Rc1 V1 aV2 jXm1 – – Ho c có th quy ñ i v dây qu n 2 jxl1/a2 jxl2 R1/a2 R2 + + aI1 I2 ZL Rc1/a2 V1 a V2 jXm1/a2 – – Bài gi ng 2 30
M ch tương ñương g n ñúng Nhánh t hóa khi n vi c tính toán khá khó khăn, do ñó nhánh này ñư c chuy n lên phía ñ u dây qu n 1, t o thành m t m ch tương ñương g n ñúng, v i sai s không ñáng k . ja2xl2 jxl1 a2R2 R1 + + I1 I2 a a2ZL aV2 V1 Rc1 jXm1 – – jx1eq R1eq + + R1eq = R1 + a 2 R2 I1 I2 a a2ZL aV2 V1 Rc1 jXm1 x1eq = xl1 + a 2 xl 2 – – Bài gi ng 2 31 Thí nghi m h m ch và ng n m ch c a MBA Các thông s trong m ch tương ñương có th ñư c xác ñ nh nh hai thí nghi m ñơn gi n: thí nghi m h m ch and thí nghi m ng n m ch. Trong các MBA công su t, các dây qu n còn ñư c g i là dây qu n cao áp (HV) và dây qu n h áp (LV). I oc W A Voc Voc IX IR V Xm Rc LV HV Thí nghi m h m ch M ch tương ñương Bài gi ng 2 32
Thí nghi m h m ch Thí nghi m ñư c th c hi n v i t t c d ng c ño phía h áp còn phía cao áp ñư c h m ch. ð t ñi n áp ñ nh m c vào phía h áp. ðo ñư c Voc, Ioc, và Poc b ng các d ng c ño. 2 Voc Voc IR = Rc = I oc = I R + I X Rc Poc I oc I X = I oc − I R 2 2 V y, Voc IX IR Voc Xm Rc Xm = IX Rc và Xm là các giá tr quy ñ i v phía h áp. Bài gi ng 2 33 Thí nghi m ng n m ch T t c d ng c ño n m phía cao áp. C p dòng ñi n ñ nh m c vào phía cao áp. ðo ñư c Vsc, Isc, và Psc b ng các d ng c ño. Xeq Req I sc W A Vsc Vsc V HV LV Psc Vsc Req = Z eq = X eq = Z eq − Req 2 2 2 I sc I sc Req và Xeq ñư c quy ñ i v phía cao áp. Bài gi ng 2 34
Ví d t i l p Vd. 3.9: Cho bi t các giá tr ño ñ c t thí nghi m h m ch và ng n m ch. Tìm các thông s m ch tương ñương quy v phía cao áp. T thí nghi m h m ch (220)2 220 IR = = 0,227 A = = 968 Ω Rc 968 50 220 I X = 12 − (0,227) = 0,974 A Xm = = 225,9 Ω 2 0,974 T thí nghi m ng n m ch 60 15 Z eq = = 0,882 Ω Req = = 0,2076 Ω (17 )2 17 X eq = 0,8822 − 0,20762 = 0,8576 Ω Bài gi ng 2 35 Hi u su t và ñ n ñ nh ñi n áp Hi u su t ñư c ñ nh nghĩa là t s gi a công su t ra và công su t vào. Pout Pout Pout η= = ×100% = ×100% Pin Pout + losses Pout + Pc + Pi Các t n hao (losses) bao g m t n hao ñ ng Pc và t n hao s t (thép) Pi. Cách khác, n u ñã bi t công su t vào, Pin − Pc − Pi η= × 100% Pin ð n ñ nh ñi n áp ñư c ñ nh nghĩa là −V Vno load – ñi n áp không t i V %∆V = no load load ×100% Vload Vload – ñi n áp khi có t i Bài gi ng 2 36