CBGD: TS. TRẦN THÀNH LONG
BÀI GIẢNG
CƠ LƯU CHẤT
TRƯỜNG ĐẠI HỌC BÁCH KHOA TP. HCM
BỘ MÔN CƠ LƯU CHẤT
I. Các khái niệm
II.Phương trình cơ bản của dòng chảy đều
III.Tổn thất năng lượng dọc đường
IV. Tổn thất năng lượng cục bộ
V.Tính toán thủy lực đường ống
CHƯƠNG 5: DÒNG CHẢY ỔN ĐỊNH TRONG ỐNG CÓ ÁP
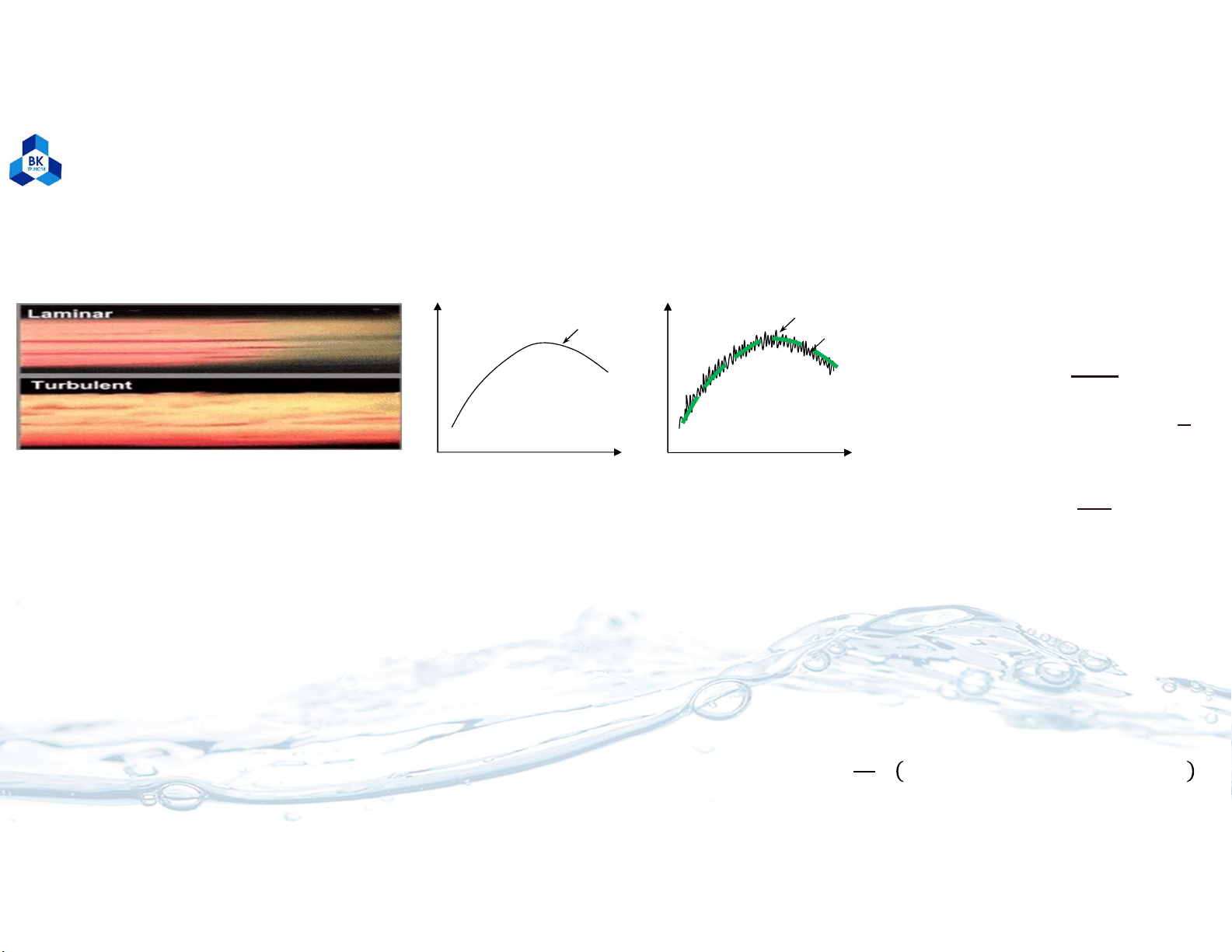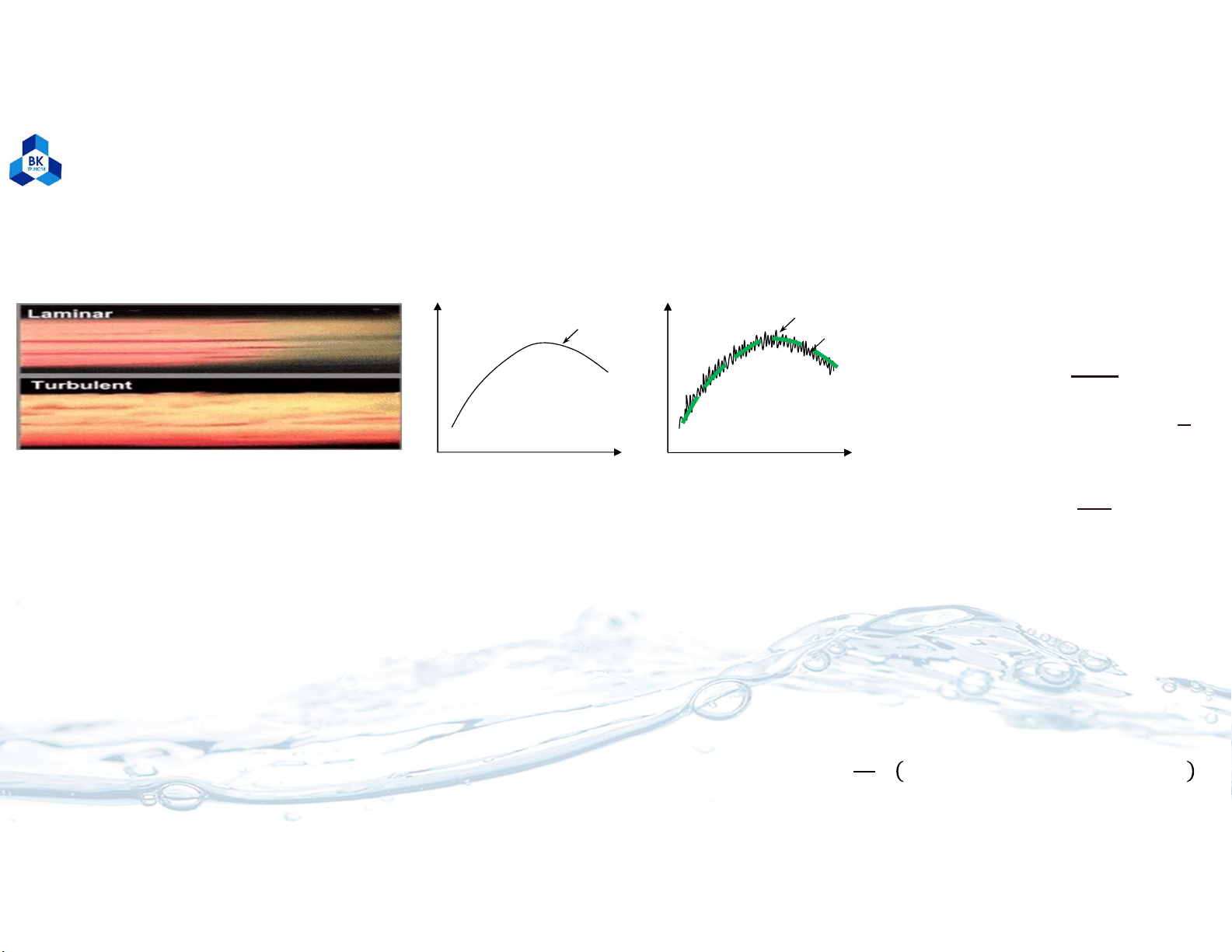
I. CÁC KHÁI NIỆM
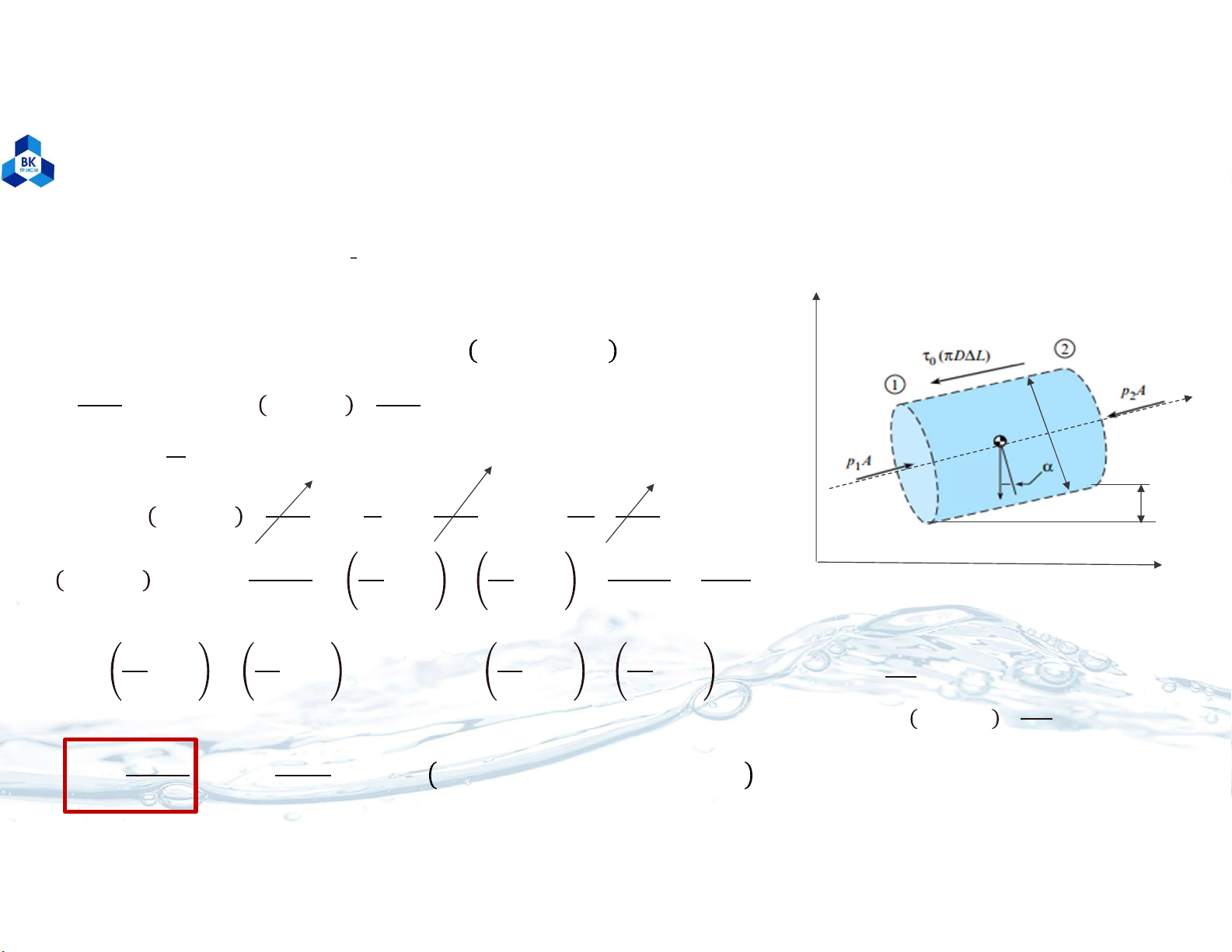
CHƯƠNG 5: DÒNG CHẢY ỔN ĐỊNH TRONG ỐNG CÓ ÁP
Chảy tầng (Laminar flow) : Re 2300
Chảy rối (Turbulent flow): Re > 2300
Với ống không phải hình tròn
𝑅𝑒 = 4𝑉𝑅
𝑣
R là bán kính thủy lực R =
Với ống không phải hình tròn
𝑅𝑒 = 𝑉𝐷
𝑣
I.1 Hai trạng thái chảy
I.2 Mô hình Boussinesq
• Phép phân tích Reynolds:
𝑢 = 𝑢 + 𝑢󰆒
(𝑢 - vận tốc trung bình thời gian; u’ – vận tốc mạch động)
•Mô hình Boussinesq:
•Các đại lượng tính toán trong dòng chảy rối là đại lượng trung bình thời gian.
•Dòng chảy rối có độ nhớt:
•𝜇 = 𝜇 + 𝜇(
eff – độ nhớt hiệu dụng ;
t– độ nhớt rối)
•Mô hình rối Prandtl (1925)
𝜇
=
𝜌
𝑙


𝑙
=
𝜅𝑦
−
𝑐ℎ𝑖ề𝑢
𝑑à𝑖
𝑥á𝑜
𝑡𝑟ộ𝑛
𝒖
t
u
(Chảy rối)
u
t
u
(Chảy tầng)
u
I.3 Lớp mỏng chảy tầng.
• Hai chế độ chảy:
–>-> chế độ chảy thành trơn thủy lực
– -> chế độ chảy thành nhám thủy lực
I. CÁC KHÁI NIỆM
CHƯƠNG 5: DÒNG CHẢY ỔN ĐỊNH TRONG ỐNG CÓ ÁP
(Lõi rối)
(Lớp mỏng chảy tầng)
𝑑,
Áp dụng phương trình năng lượng ta có
𝒑𝟏
𝜸+ 𝒛𝟏=𝒑𝟐
𝜸+ 𝒛𝟐+ 𝒉𝒇⇒ 𝒉𝒇=𝒑𝟏
𝜸+ 𝒛𝟏−𝒑𝟐
𝜸+ 𝒛𝟐
Thế hf vào phương trình động năng
𝒉
𝒇
=
𝟒∆𝑳𝝉𝟎
𝑫𝜸
⇒
𝝉
𝟎
=
𝑫𝒉𝒇𝜸
𝟒
∆
𝑳
=
𝜸
𝑹
𝑱
𝐽
=
ℎ
∆
𝑙
⁄
→
đ
ộ
𝑑ố𝑐
𝑡ℎủ𝑦
𝑙ự𝑐
⇒ 𝜸 𝝅𝑫𝟐
𝟒∆𝑳 ∗ 𝐬𝐢𝐧 ∝ + 𝒑𝟏− 𝒑𝟐∗𝝅𝑫𝟐
𝟒− 𝝉𝟎𝝅𝑫∆𝑳 = 𝟎
Ta có 𝐬𝐢𝐧 ∝= ∆𝒛
∆𝑳
𝒑𝟏− 𝒑𝟐∗𝝅𝑫𝟐
𝟒− 𝝉𝟎
𝟒
𝑫∆𝑳 ∗ 𝝅𝑫𝟐
𝟒− 𝜸∆𝑳 ∗ ∆𝒛
∆𝑳 ∗𝝅𝑫𝟐
𝟒= 𝟎
II. PHƯƠNG TRÌNH CƠ BẢN CỦA DÒNG CHẢY ĐỀU
CHƯƠNG 5: DÒNG CHẢY ỔN ĐỊNH TRONG ỐNG CÓ ÁP
Phương trình biến thiên động lượng của thể tích kiểm soát giới hạn bởi 2 mặt
cắt 1 và 2 trên phương S
𝐺+ 𝑃− 𝑃− 𝐹
 = 𝜌𝑄 𝛽𝑉− 𝛽𝑉
= 0
z
x
h
Ngoại lực tác dụng trên phương chuyển động:
•Gs=𝜸𝝅𝑫𝟐
𝟒∆𝑳 ∗ 𝐬𝐢𝐧 ∝ - trọng lực
•P1- P2=𝒑𝟏− 𝒑𝟐∗𝝅𝑫𝟐
𝟒– áp lực
•Fms =𝝉𝟎𝝅𝑫∆𝑳– lực msát trên vỏ ống
𝝉
𝟎
ứng suất ma sát tại vỏ ống
s
𝒑𝟏− 𝒑𝟐− 𝜸∆𝒛 = 𝟒∆𝑳𝝉𝟎
𝑫⇒𝒑𝟏
𝜸+ 𝒛𝟏−𝒑𝟐
𝜸+ 𝒛𝟐=𝟒∆𝑳𝝉𝟎
𝜸𝑫 =∆𝑳𝝉𝟎
𝜸𝑹
II.1 Phương trình cơ bản.
Gsz
D