CBGD: TS. TRẦN THÀNH LONG
BÀI GIẢNG
CƠ LƯU CHẤT
TRƯỜNG ĐẠI HỌC BÁCH KHOA TP. HCM
BỘ MÔN CƠ LƯU CHẤT
I. Các khái niệm.
II. Các chuyển động có thế phẳng cơ bản.
III.Một số chuyển động được tạo bởi phép chồng chất
CHƯƠNG 7: CHUYỂN ĐỘNG PHẲNG CÓ THẾ
CHƯƠNG 7: CHUYỂN ĐỘNG PHẲNG CÓ THẾ
1.1 Chuyển động có thế
Đn: Chuyển động của lưu chất được gọi là có thế khi tồn tại một hàm sao cho:
𝑢 = 𝑔𝑟𝑎𝑑 𝜑
- hàm thế vận tốc; Đường cong (x,y) = const – Đường đẳng thế
• Tính chất:
𝜔 = 1
2𝑟𝑜𝑡 𝑢 = 0
• Phương trình:
xuyu yx
;
2112
q
1.2 Hàm dòng
Đn: Hàm (x,y) sao cho được gọi là hàm dòng.
Đường cong (x,y) = const là đường dòng
• Tính chất:
• Phương trình:
q12
ψ1
ψ2
I. Các khái niệm
;
CHƯƠNG 7: CHUYỂN ĐỘNG PHẲNG CÓ THẾ
I. Các khái niệm
1.3 Hàm thế phức.
• Hàm dòng và hàm thế có tính trực giao do:
𝑔𝑟𝑎𝑑 𝜑 • 𝑔𝑟𝑎𝑑 𝜓 =
+
= 0
1.4 Tính chồng chất.
𝑓 𝑧 = 𝑓
𝑧 + 𝑓
𝑧
𝜙 𝑥, 𝑦 = 𝜙𝑥, 𝑦 + 𝜙𝑥, 𝑦
𝜓 𝑥, 𝑦 = 𝜓𝑥, 𝑦 + 𝜓𝑥, 𝑦
𝑢 𝑥, 𝑦 = 𝑢𝑥, 𝑦 + 𝑢𝑥, 𝑦
mô tả chuyển động có thế bằng hàm thế phức:
𝑓 𝑧 = ϕ + 𝑖𝜓 = 𝑟𝑒
•Các đại lượng:
𝑉 𝑧 = 𝑢𝑥, 𝑦 + 𝑖𝑢𝑥, 𝑦 → 𝒗ậ𝒏 𝒕ố𝒄 𝒑𝒉ứ𝒄
𝑉
𝑧 =
= 𝑢𝑥, 𝑦 − 𝑖𝑢𝑥, 𝑦 → vận tốc liên hợp với vận tốc phức
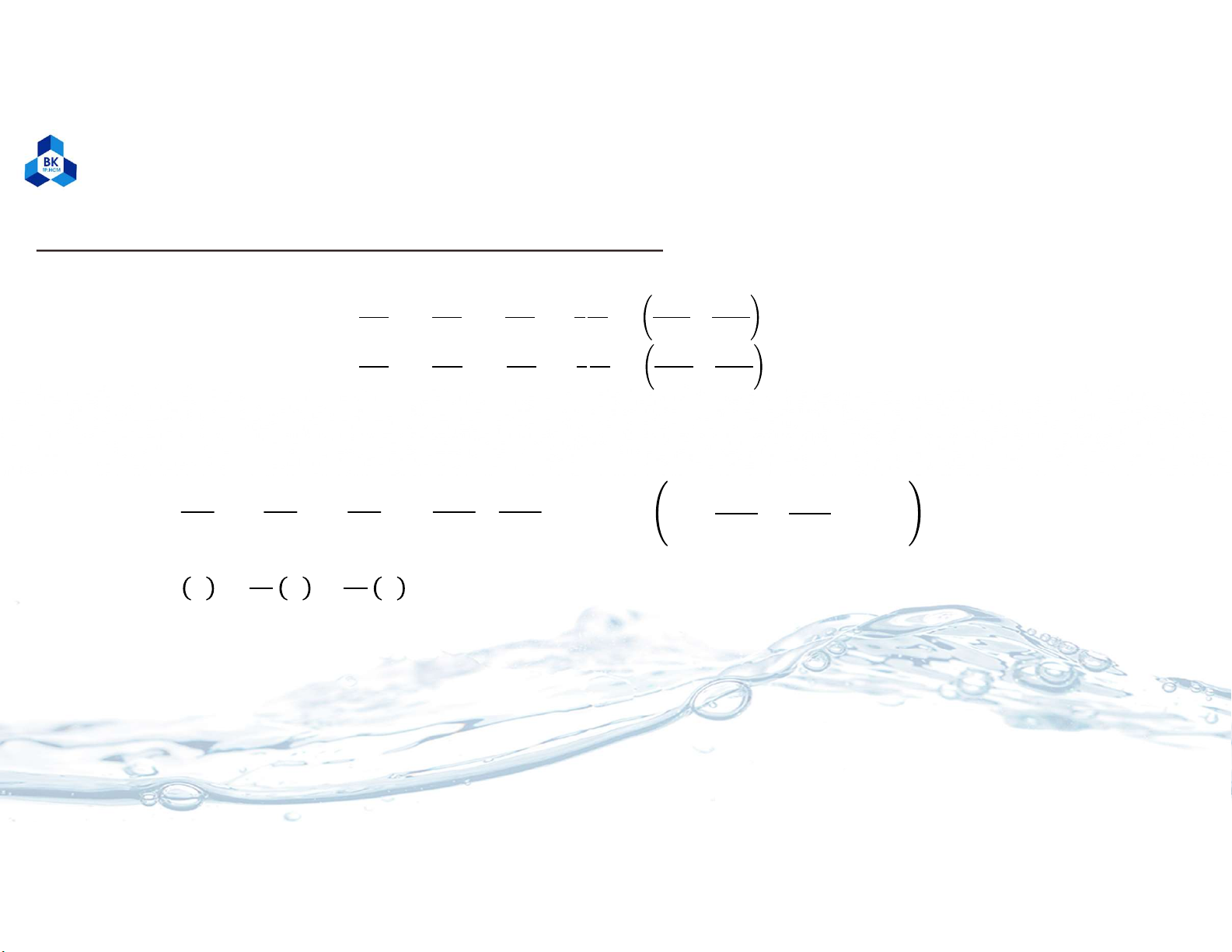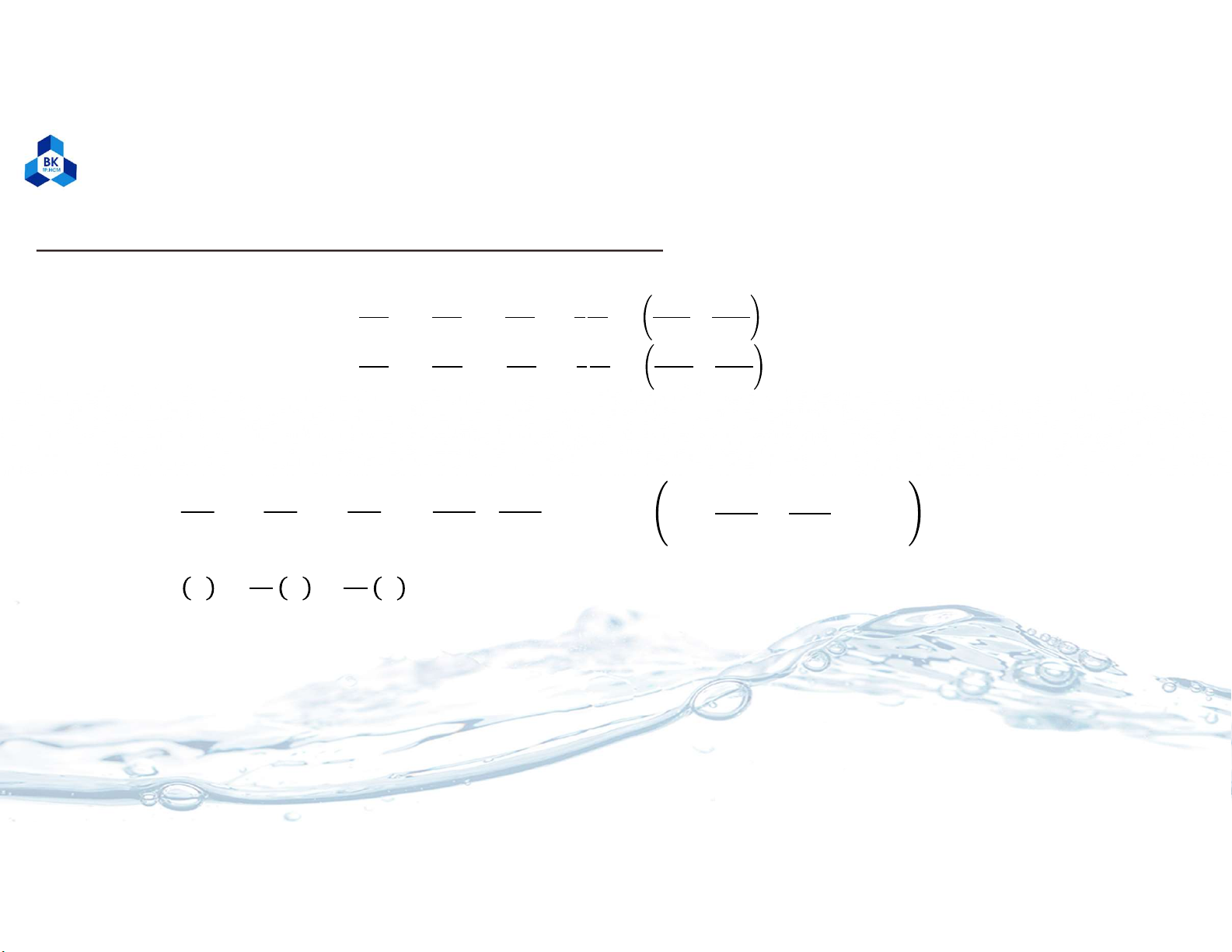
CHƯƠNG 7: CHUYỂN ĐỘNG PHẲNG CÓ THẾ
I. Các khái niệm
1.5 Phương trình Navier-Stokes dạng hàm xoáy – hàm dòng.
• Phương trình Navier-Stokes 2 chiều:
𝜕𝑢
𝜕𝑡 + 𝑢
𝜕𝑢
𝜕𝑥 + 𝑢
𝜕𝑢
𝜕𝑦 = − 1
𝜌
𝜕𝑝
𝜕𝑥 + 𝜈 𝜕𝑢
𝜕𝑥+𝜕𝑢
𝜕𝑦+ 𝐹
𝜕𝑢
𝜕𝑡 + 𝑢
𝜕𝑢
𝜕𝑥 + 𝑢
𝜕𝑢
𝜕𝑦 = − 1
𝜌
𝜕𝑝
𝜕𝑦 + 𝜈 𝜕𝑢
𝜕𝑥+𝜕𝑢
𝜕𝑦+ 𝐹
• Khi chuyển động là có thế: 0
(3) thỏa mãn tự động;
(4) thành pt Laplace cho hàm dòng
• Dạng hàm xoáy – hàm dòng:
2
2
2
2
yxy
u
x
u
tyx
𝜁 = 𝜕𝑢
𝜕𝑥 −𝜕𝑢
𝜕𝑦 = 2𝜔(3)
• Phương trình cho hàm xoáy:
• Phương trình cho hàm dòng:
Δ𝜓 = −𝜁 (4)
(3 =
2 −
1cùng đk: lực khối có thế).
(1)
(2)
