150
Chương 7: Dự trữ ổn định của hệ thống điều khiển
Các khái niệm về dự trữ ổn định
•Dự trữ ổn định của một hệ thống điều khiển là khái niệm phản ánh mức
độ dự phòng nhằm đảm bảo cho hệ thống ổn định chắc chắn.
•Về mặt toán học, dự trữ ổn định là một đại lượng đảm bảo cho các
nghiệm đặc tính của hệ thống nằm lùi về bên trái trục ảo một khoảng
nhất định
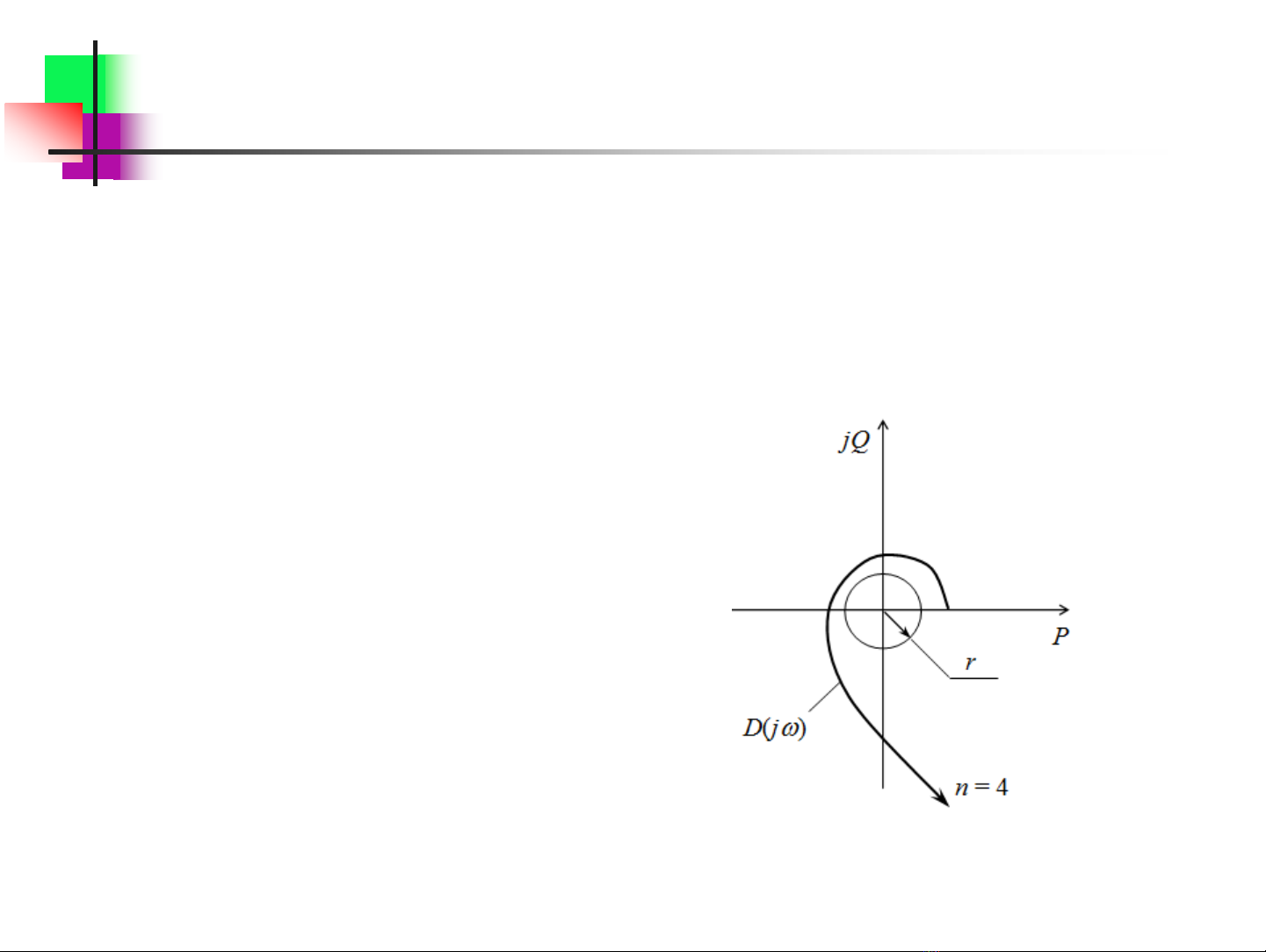
Ví dụ, theo tiêu chuẩn Hurvit, hệ thống có
dự trữ ổn định nếu các định thức Hurvit
thoả mãn điều kiện i – 0, i =1,2, ...,n,
trong đó i là các định thức Hurvit; n - bậc
của đa thức đặc tính
151
Chương 7: Dự trữ ổn định của hệ thống điều khiển
Dự trữ ổn định theo Pha và Biên độ của hệ
a gọi là dự trữ biên độ
gọi là dự trữ pha
Cách xác định dự trữ ổn định của hệ thống
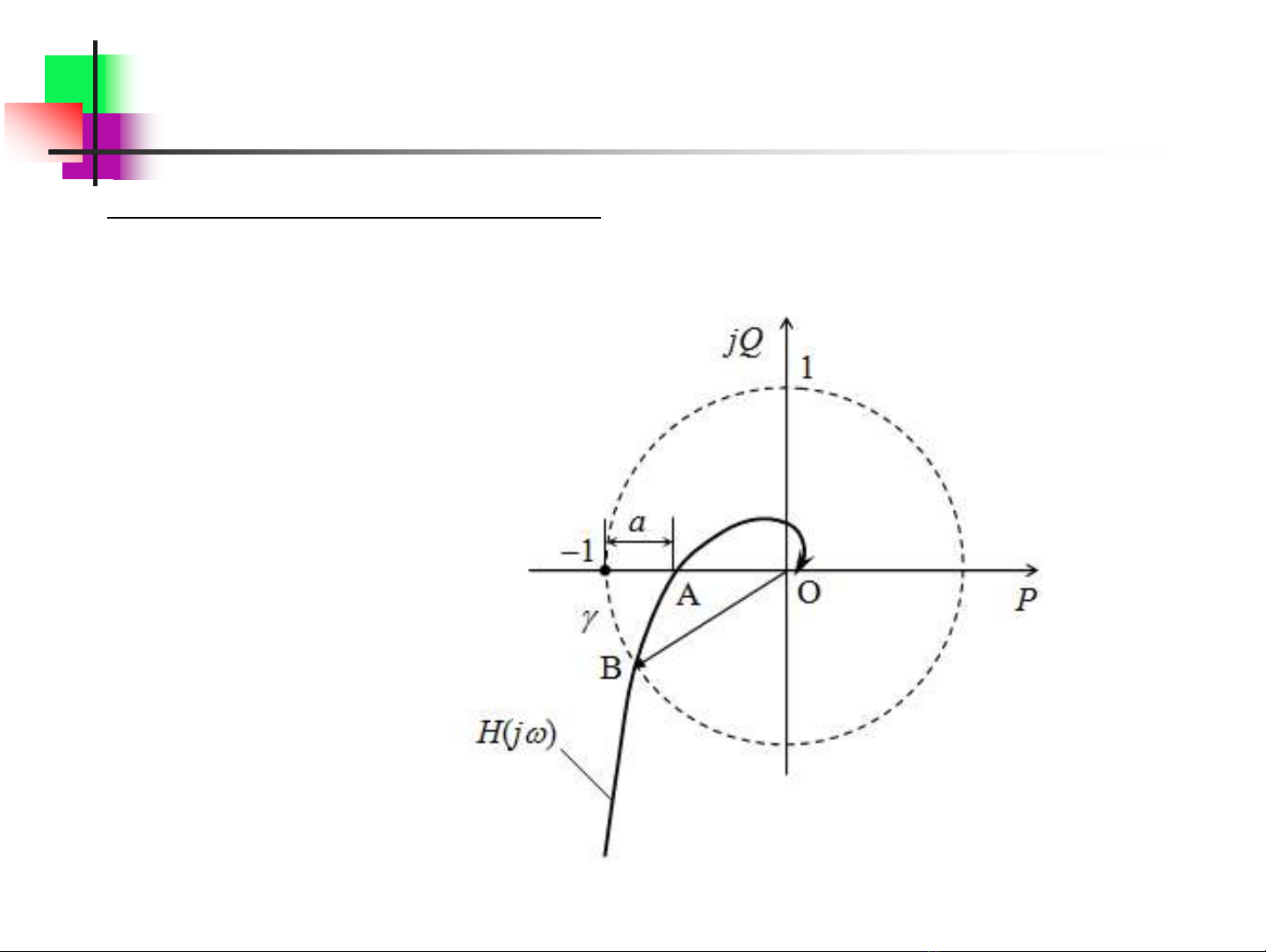
Hệ quả của tiêu chuẩn ổn định Nyquist:
Một hệ thống ổn định ở trạng thái hở, thì sẽ ổn định ở trạng thái kín, nếu đặc tính tần
số H(j
) của hệ hở không bao điểm (
1,j0).
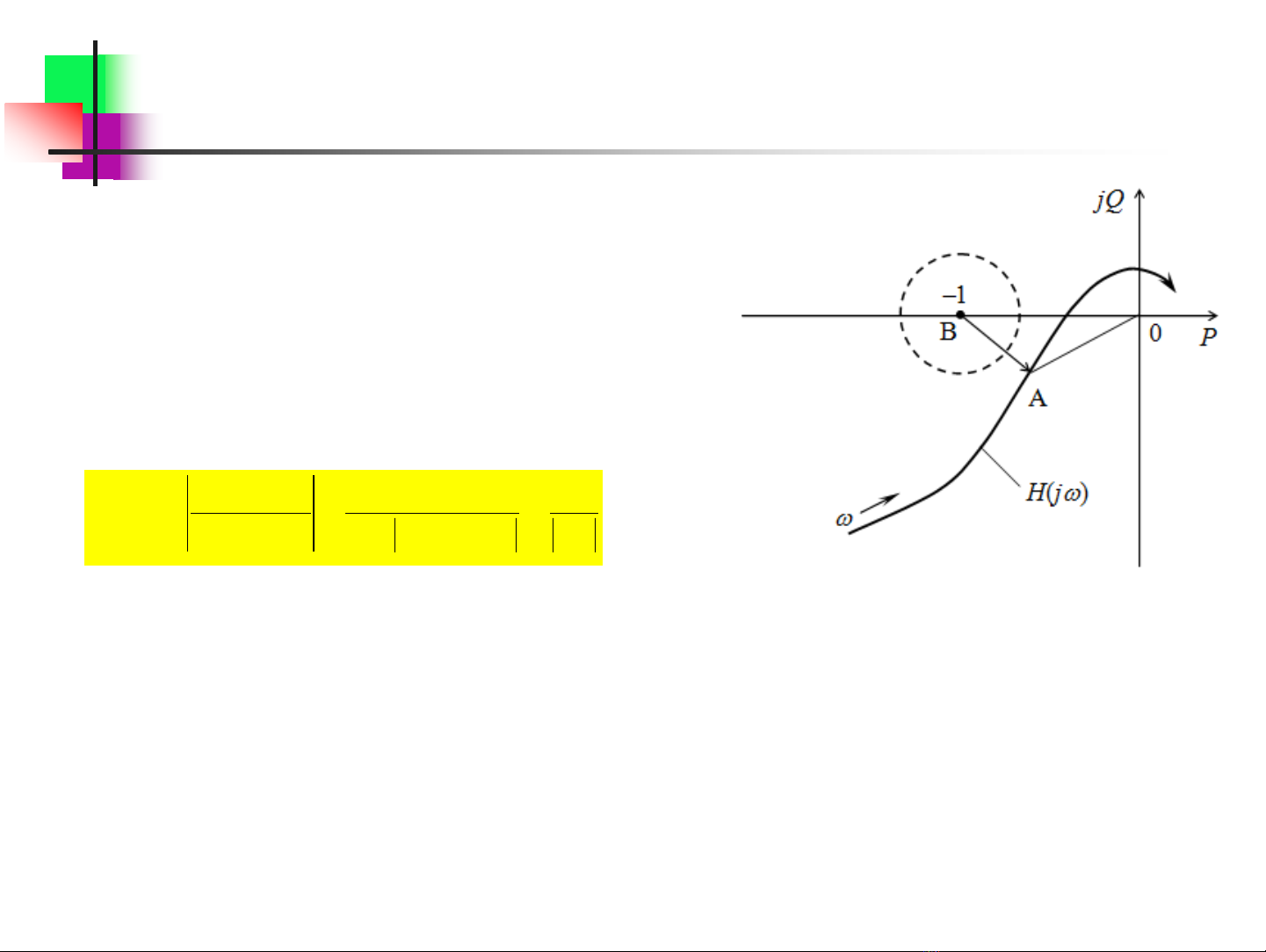
Độ nhạy của hệ thống là độ khuếch đại lớn nhất
của hệ thống, ứng với tần số cộng hưởng.
Tín hiệu đầu vào dao động với tần số cộng
hưởng sẽ gây ra sai số điều chỉnh lớn nhất
Giả sử hệ hở là ổn định, độ nhạy của hệ thống
kín:
152
Chương 7: Dự trữ ổn định của hệ thống điều khiển
Dự trữ ổn định theo độ nhạy của hệ thống
ABjHjH
S1
)(1min
1
)(1
1
max
Đặc tính tần số biên độ pha của hệ hở
Điều kiện để hệ kín thống có độ nhạy hữu hạn là đặc tính H(j
) của hệ hở
không bao và không cắt vòng tròn “cấm” nhất định với tâm là điểm tới hạn
153
Chương 7: Dự trữ ổn định của hệ thống điều khiển
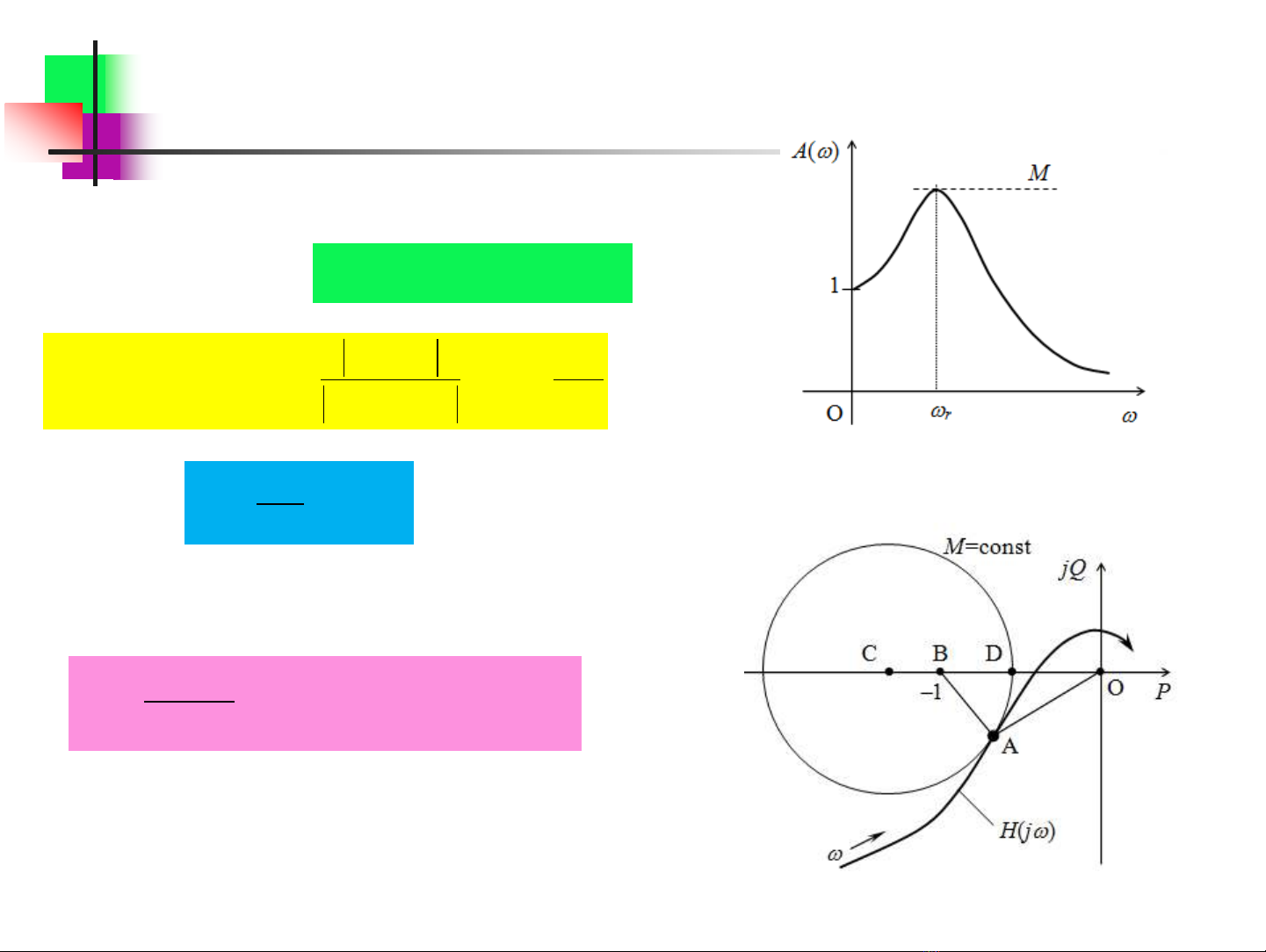
Dự trữ ổn định theo chỉ số biên độ
Đặc tính biên độ của hệ kín
Đặc tính biên độ pha của hệ hở
)()(max r
AAM
BA
OA
max
)(1
)(
sup)(sup
jH
jH
AM
const
OB
OA
M
•Điều kiện đảm bảo dự trữ ổn định theo chỉ
số biên độ cho trước
() ,
(0 0
)
rZ Z
AM constMM
A
•Đối với đa số các hệ điều khiển trong công
nghiệp: |H(j0)| = ; A(0) = 1
•Điểm cộng hưởng được đặc trưng bởi chỉ số
biên độ được tính:
Chương 7: Dự trữ ổn định của hệ thống điều khiển
Dự trữ ổn định theo độ ổn định
154
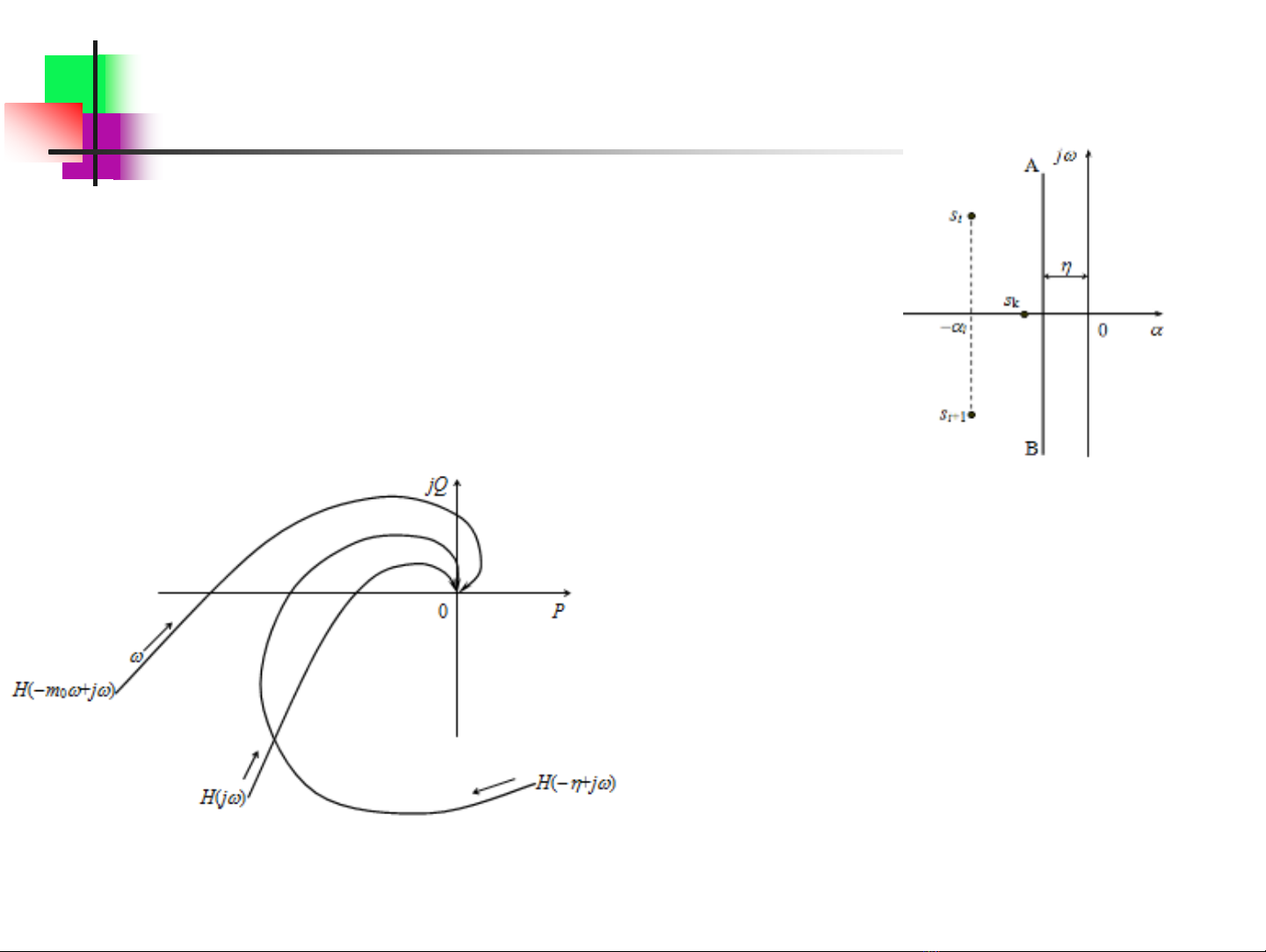
Sự phân bố các nghiệm
đặc tính của hệ thống
Thay s =
+ j
vào hàm truyền của hệ hở, ta được
đặc tính tần số mở rộng loại I:
H(
+ j
)
gọi là đặc tính mở rộng của hệ hở theo độ
ổn định
Các đường cong ánh xạ trên hệ tọa độ cực từ
các đường biên giới hạn nghiệm
Tiêu chuẩn dự trữ ổn định dựa trên tiêu chuẩn
ổn định Nyquist : Điều kiện cần và đủ để các
nghiệm đặc tính của hệ kín nằm bên trái đường
thẳng đứng AB (cách trục ảo một khoảng
), là
đặc tính mở rộng H(

+j
) của hệ hở bao
điểm (
1;j0) ngược chiều kim đồng hồ q/2 lần,
khi
=0
+
, trong đó, q - số nghiệm nằm
bên phải AB