Cây AVL
Đánh giá tìm ki mế
1
1, 2, 3, 4, 5 1
2
3
4
5
Cây AVL
Gi i thi u AVL Treeớ ệ
Ph ng pháp chèn ươ trên CNPTK có th có nh ng bi n d ng ể ữ ế ạ
m t cân đi nghiêm tr ngấ ố ọ
Chi phí cho vi c tìm ki m ệ ế trong tr ng h p x u nh t đt t i ườ ợ ấ ấ ạ ớ
n
VD: 1 tri u ệnút ⇒chi phí tìm ki m =ế 1.000.000 nút
N u có m t cây tìm ki m nh phân cân b ng hoàn toàn, ế ộ ế ị ằ chi
phí cho vi c tìm ki m ệ ế ch x p x ỉ ấ ỉ log2n
VD: 1 tri u ệnút ⇒chi phí tìm ki m =ế log21.000.000 20 nút≈
G.M. Adelson-Velsky và E.M. Landis đã đ xu t m t tiêu ề ấ ộ
chu n cân b ng (sau này g i là cân b ng ẩ ằ ọ ằ AVL)
Cây AVL có chi u cao O(logề2(n))
2
Cây AVL
AVL Tree - Đnh nghĩaị
3
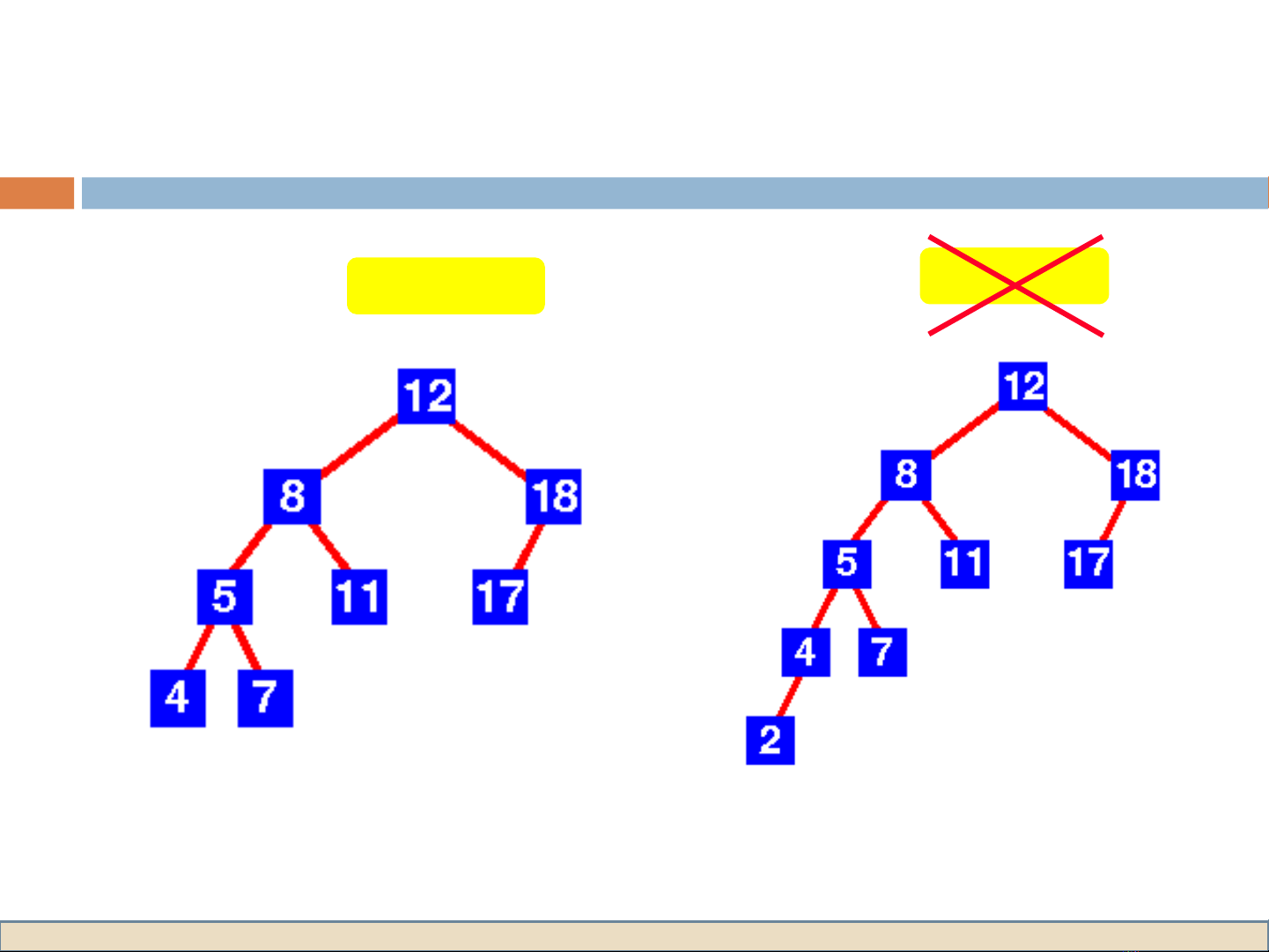
Cây nh phân tìm ki m cân b ng (AVL) là cây mà ị ế ằ t i m i ạ ỗ
nút đ cao ộc a cây con trái và c a cây con ph i ủ ủ ả chênh l ch ệ
không quá m tộ44
23 88
13 37 59 108
15 30 40 55 71
Cây AVL
AVL Tree – Ví dụ
4
AVL Tree ? AVL Tree?
Cây AVL
AVL Tree
Ch s cân b ng c a m t nút: ỉ ố ằ ủ ộ
Đnh nghĩaị: Ch s cân b ng c a m t nút là ỉ ố ằ ủ ộ hi uệ c a chi u cao ủ ề
cây con ph i và cây con trái c a nóả ủ
Đi v i m t cây cân b ng, ch s cân b ng (CSCB) c a m i ố ớ ộ ằ ỉ ố ằ ủ ỗ
nút ch có th mang m t trong ba giá tr sau đây: ỉ ể ộ ị
CSCB(p) = 0 Đ cao cây ph i (p) = Đ cao cây trái (p)ộ ả ộ
CSCB(p) = 1 Đ cao cây ph i (p) > Đ cao cây trái (p)ộ ả ộ
CSCB(p) = -1 Đ cao cây ph i (p) < Đ cao cây trái (p)ộ ả ộ
5