
(c) SE/FIT/HUT 2002
Đường cong trong không gian
3D CURVE
(c) SE/FIT/HUT 2002 2
Đường cong - Curve
Why use curves? Quỹ đạo chuyển động của 1 điểm trong
không gian
Đường cong biểu diễnĐiểm-curve represents points:
ĐiểmBiểu diễnvà kiểm soát đường cong -Points represent-
and control-the curve.
Cách tiếp cận này là cơ sởcủa lĩnh vực Computer Aided Geometric
Design (CAGD).
(c) SE/FIT/HUT 2002 3
Phân loại
Trên cơ sởràng buộc giữa điểm và đường trong cảứng dụng khoa học và
thiết kếta co thểphân làm 2 loại:
Xấp xỉ-Approximation -
Được ứng dụng trong mô hình hoá hình học
Nội suy-Interpolation
Trong thiết kếnôi suy là cần thiết với các đối tượng nhưng không phù hợp
với các đối tượng có hình dáng bất kỳ"free form“.
(c) SE/FIT/HUT 2002 4
Biểu diễn Đường cong
Tường minh y=f(x)
y = f(x), z = g(x)
impossible to get multiple values for a single
x
•break curves like circles and ellipses
into segments
not invariant with rotation
•rotation might require further segment
breaking
problem with curves with vertical tangents
•infinite slope is difficult to represent
Không tường minh f(x,y)=0 - Implicit equations:
f(x,y,z) = 0
equation may have more solutions than we
want
•circle: x² + y² = 1, half circle: ?
problem to join curve segments together
•difficult to determine if their tangent
directions agree at their joint point
(c) SE/FIT/HUT 2002 5
Đường cong tham biến
Biểu diễn các đường cong tham biến Parametric representation:
x = x(t), y = y(t), z = z(t)
overcomes problems with explicit and implicit forms
no geometric slopes (which may be infinite)
parametric tangent vectors instead (never infinite)
a curve is approximated by a piecewise polynomial curve
Define a parameter space
1D for curves
2D for surfaces
Define a mapping from parameter space to 3D points
A function that takes parameter values and gives back 3D points
The result is a parametric curve or surface
0t
1
Mapping F :t →(x, y, z)
(c) SE/FIT/HUT 2002 6
Parametric Curves
We have seen the parametric form for a line:
Note that x, y and z are each given by an equation that
involves:
The parameter t
Some user specified control points, x0and x1
This is an example of a parametric curve
10
10
10
)1(
)1(
)1(
zttzz
yttyy
xttxx
−+=
−+=
−+
=

(c) SE/FIT/HUT 2002 7
Đường cong đa thức bậc ba
Phảiđảmbảolàđường cong không gian với3 trụctoạđộx, y, z
tránh đượcnhững tính toán phứctạpvànhững phầnnhấp nhô ngoài ý
muốnxuấthiệnởnhững đường đathứcbậc cao
Why cubic?
(c) SE/FIT/HUT 2002 8
P0
P1 p2
p3
P0
P'0 P1
P'1
Đường cong bậc3
x= a1+ b1u+ c1u2+ d1u3
y= a2+ b2u+ c2u2+ d2u3
z= a3+ b3u+ c3u2+ d3u3
Với3 điểmP0, P1, P2, P3 phương trình
xác định
(c) SE/FIT/HUT 2002 9
Hermite Spline
A spline is a parametric curve defined by control points
The term spline dates from engineering drawing, where a spline was a piece
of flexible wood used to draw smooth curves
The control points are adjusted by the user to control the shape of the curve
Phương pháp Hermite dựa trên cơ sởcủa cách biểu diễn Ferguson hay Coons
năm 60
AHermite spline is a curve for which the user provides:
The endpoints of the curve
The parametric derivatives of the curve at the endpoints
•The parametric derivatives are dx/dt, dy/dt, dz/dt
That is enough to define a cubic Hermite spline, more derivatives are required
for higher order curves
(c) SE/FIT/HUT 2002 10
Đường cong Hermite
p = p(u) = k0+ k1u + k2u2+ k3u3
p(u) = ∑kiui i∈n
p0 và p1ta có hai độ dốc p0’vàp
1’với u = 0 và u = 1 tại hai
điểm đầu cuối của đoạn [0,1].
We have constraints:
The curve must pass through p0when u=0
The derivative must be p’0when u=0
The curve must pass through p1when u=1
The derivative must be p’1when u=1
(c) SE/FIT/HUT 2002 11
Basis Functions
A point on a Hermite curve is obtained by multiplying each control point
by some function and summing
The functions are called basis functions
(c) SE/FIT/HUT 2002 12
Thay vào:
p= p(u) = p0(1-3u2+2u3) + p1(3u2-2u3)
+ p0’(u-2u2+u3) + p1’(-u2+u3)
p = p(u) = [ 1 u u2 u3]

(c) SE/FIT/HUT 2002 13
Đường cong Bezier
Sửdụng điểm và các vector kiểmsoátđượcđộ dốccủađường
cong tạinhưng điểmmànóđiqua.(Hermit)
không đượcthuậnlợi cho việcthiếtkếtương tác, không tiếpcận
vào các độ dốccủađường cong bằng các giá trịsố(Hermite).
Paul Bezier,RENAULT, 1970 đường và bềmặt UNISURF
(c) SE/FIT/HUT 2002 14
po, p3 tương đương với p0, p1 trên đường Hermite. diểm trung
gian p1, p2 được xác định bằng 1/3 theo độ dài của vector tiếp
tuyến tại điểm po và p3
p0’= 3(p
1–p
0)
p3’= 3(p
3–p
2)
p = p(u) = p0(1-3u2+2u3) + p1(3u2-2u3) + p0’(u-2u2+u3) + p1’(-
u2+ u3)
p = p(u) = p0(1 - 3u + 3u2-u
3) + p1(3u-6u2-3u3)
+ p2(3u2-3u
3) + p3u3
(c) SE/FIT/HUT 2002 15
Biểu diễn Ma trận
p = p(u) = [ 1 u u2u3]
−−
−
−
3
2
1
0
1331
0363
0033
0001
p
p
p
p
0
0.2
0.4
0.6
0.8
1
1.2
B0
B1
B2
B3
(c) SE/FIT/HUT 2002 16
Ưuđiểm
dễdàng kiểm soát hi`nh dạng của đường cong hơn vector tiếp
tuyến tại p0’vàp
1’của Hermite.
Nằm trong đa giác kiểm soát với số điểm trung gian tuỳý( số
bậc tuỳ ý)
đi qua điểm đầu và điểm cuối của đa giác kiểm soát, tiếp xúc với
cặp hai vector của đầu cuối đó
(c) SE/FIT/HUT 2002 17
Example
Bezier Curves
[UW]
(c) SE/FIT/HUT 2002 18
Sub-Dividing Bezier Curves
P0
P1P2
P3
M01
M12
M23
M012 M123
M0123
(c) SE/FIT/HUT 2002 19
Sub-Dividing Bezier Curves
P0
P1P2
P3
(c) SE/FIT/HUT 2002 20
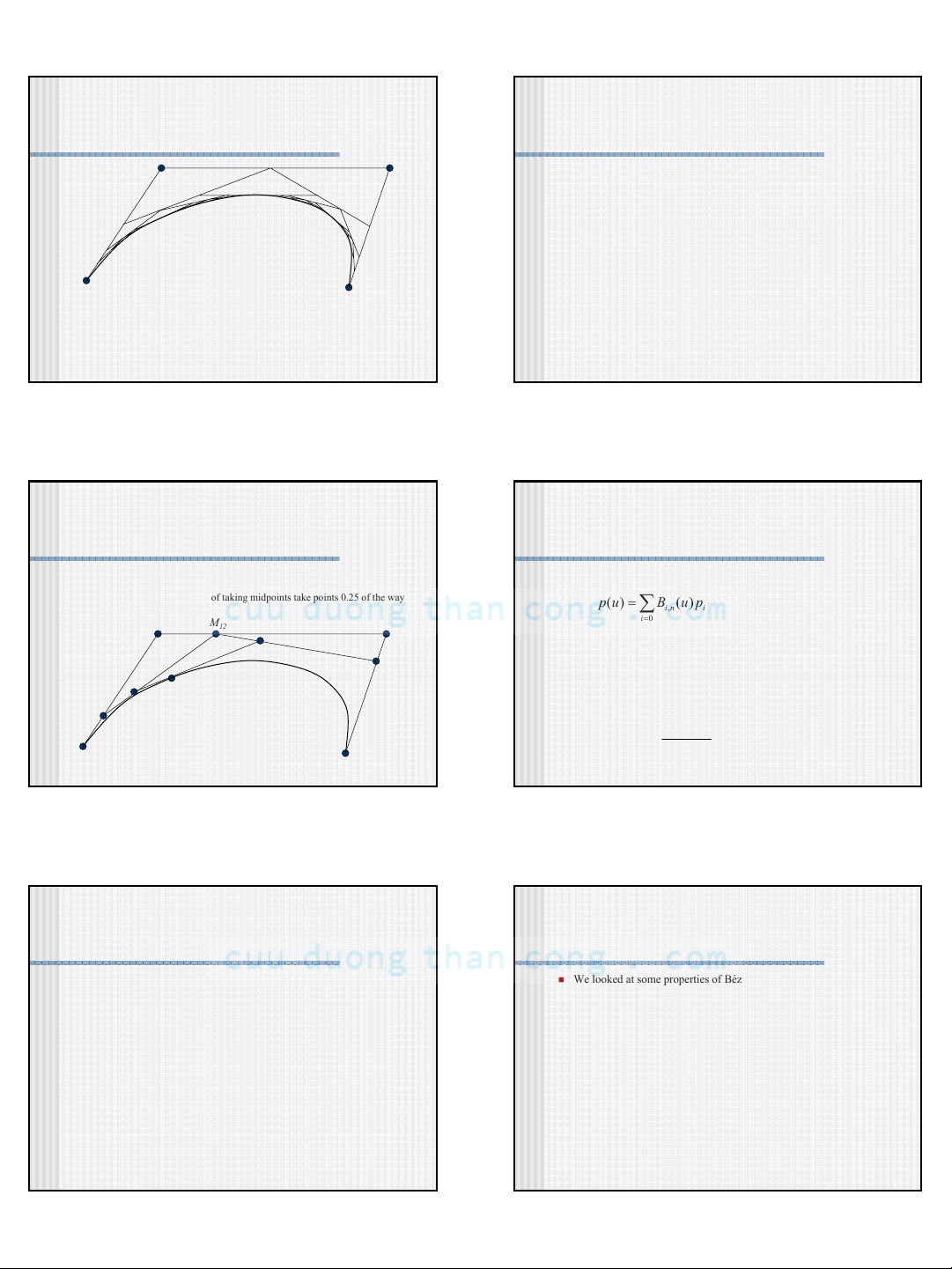
Sub-Dividing Bezier Curves
Step 1: Find the midpoints of the lines joining the original control vertices.
Call them M01, M12, M23
Step 2: Find the midpoints of the lines joining M01, M12 and M12, M23. Call
them M012, M123
Step 3: Find the midpoint of the line joining M012, M123. Call it M0123
The curve with control points P0, M01, M012 and M0123 exactly follows the
original curve from the point with t=0 to the point with t=0.5
The curve with control points M0123 , M123 , M23 and P3exactly follows the
original curve from the point with t=0.5 to the point with t=1
(c) SE/FIT/HUT 2002 21
de Casteljau’s Algorithm
You can find the point on a Bezier curve for any parameter value twith a similar
algorithm
Say you want t=0.25, instead of taking midpoints take points 0.25 of the way
P0
P1P2
P3
M01
M12
M23
t=0.25
(c) SE/FIT/HUT 2002 22
BiểuthứcBezier-Bernstain
Tổng quát hoá vớin+1 điểmkiểm soát
p0... pn : vector vịtrí củađagiácn+1 đỉnh
))(()(
)()(
1
0
1,
0
,
ii
n
i
ni
i
n
i
ni
PpuBnup
puBup
−=
′
=
+
=
−
=
∑
∑
ini
ni uuinCuB −
−= )1(),()(
,
)!in(!i
!n
)i,n(C −
=
(c) SE/FIT/HUT 2002 23
Tính chất
P0 và Pn nằm trên đường cong.
Đường cong liên tục và có đạo hàm liên tục tất cảcác bậc
Tiếp tuyến của đường cong tại điểm P0 là đường P0P1 và tại
Pn là đường Pn-1Pn .
Đường cong nằm trong đường bao lồi convex hull của các
điểm kiểm soát.
This is because each successive Pi(j) is a convex
combination of the points Pi(j-1) and Pi-1(j-1) .
P1 ,P2 , … ,Pn-1 nằm trên đường cong khi và chỉ khi
đường cong là đoạn thẳng.
(c) SE/FIT/HUT 2002 24
Review:
Bézier Curve Prop’s [1/6]
We looked at some properties of Bézier curves.
Generally “Good” Properties
Endpoint Interpolation
Smooth Joining
Affine Invariance
Convex-Hull Property
Generally “Bad” Properties
Not Interpolating
No Local Control

(c) SE/FIT/HUT 2002 25
Problem with Bezier Curves
To make a long continuous curve with Bezier segments
requires using many segments
Maintaining continuity requires constraints on the control
point positions
The user cannot arbitrarily move control vertices and automatically
maintain continuity
The constraints must be explicitly maintained
It is not intuitive to have control points that are not free
(c) SE/FIT/HUT 2002 26
Invariance
Translational invariance means that translating the control points and then
evaluating the curve is the same as evaluating and then translating the curve
Rotational invariance means that rotating the control points and then evaluating
the curve is the same as evaluating and then rotating the curve
These properties are essential for parametric curves used in graphics
It is easy to prove that Bezier curves, Hermite curves and everything else we will
study are translation and rotation invariant
Some forms of curves, rational splines, are also perspective invariant
Can do perspective transform of control points and then evaluate the curve
(c) SE/FIT/HUT 2002 27
Longer Curves
A single cubic Bezier or Hermite curve can only capture a small class of curves
At most 2 inflection points
One solution is to raise the degree
Allows more control, at the expense of more control points and higher degree
polynomials
Control is not local, one control point influences entire curve
Alternate, most common solution is to join pieces of cubic curve together into
piecewise cubic curves
Total curve can be broken into pieces, each of which is cubic
Local control: Each control point only influences a limited part of the curve
Interaction and design is much easier
(c) SE/FIT/HUT 2002 28
Piecewise Bezier Curve
“knot”
P0,0
P0,1 P0,2
P0,3
P1,0
P1,1
P1,2
P1,3
(c) SE/FIT/HUT 2002 29
Continuity
When two curves are joined, we typically want some degree of continuity
across the boundary (the knot)
C0, “C-zero”, point-wise continuous, curves share the same point where they
join
C1, “C-one”, continuous derivatives, curves share the same parametric
derivatives where they join
C2, “C-two”, continuous second derivatives, curves share the same parametric
second derivatives where they join
Higher orders possible
Question: How do we ensure that two Hermite curves are C1across a
knot?
Question: How do we ensure that two Bezier curves are C0, or C1, or C2
across a knot?
(c) SE/FIT/HUT 2002 30
Đường bậc ba Spline
Spline đi qua n điểm cho trước mà mỗi đoạn là đường bậc ba
độc lập có độ dốc và độ cong liên tục tại mỗi điểm kiểm soát
hay điểm nút
Với n điểm:n-1 đoạn với mỗi đoạn 4 vector hệsố 4(n-1) cho
n-1 đoạn, và 2(n-1) điều kiện biên và n-2 điều kiện về độ dốc
cùng n-2 về độ cong
Spline dùng để chỉ phương pháp biểu diễn đường cong mềm
thông qua các đoạn cong tham biến bậc ba với các điều kiện
liên tục tại các điểm đầu nút




![Bài giảng Đồ hoạ kỹ thuật 1: Phần 1 - Trường ĐH Thuỷ Lợi [Mới Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230131/baphap06/135x160/672431589.jpg)


![Bài giảng Lập trình trực quan: Tổng hợp kiến thức [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20221025/minhtam37847/135x160/684443159.jpg)











![SQL: Ngôn Ngữ Truy Vấn Cấu Trúc và DDL, DML, DCL [Hướng Dẫn Chi Tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250812/kexauxi10/135x160/13401767990844.jpg)




![Hệ Thống Cơ Sở Dữ Liệu: Khái Niệm và Kiến Trúc [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250812/kexauxi10/135x160/89781767990844.jpg)
![Hệ Cơ Sở Dữ Liệu: Tổng Quan, Thiết Kế, Ứng Dụng [A-Z Mới Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250812/kexauxi10/135x160/61361767990844.jpg)
