Bài giảng Giải tích 1 (Calculus 1): Hàm số lượng giác ngược - TS. Đào Huy Cường

Tài liệu này cung cấp một cái nhìn tổng quan về các khái niệm cơ bản trong Giải tích 1, tập trung vào định nghĩa và tính chất của các loại hàm số quan trọng cùng với khái niệm giới hạn.

Sinh viên và học viên đang theo học môn Giải tích 1 hoặc các khóa học liên quan đến toán ứng dụng, đặc biệt là những người cần tài liệu tham khảo về hàm số lượng giác ngược, hàm số hyperbolic và giới hạn hàm số.

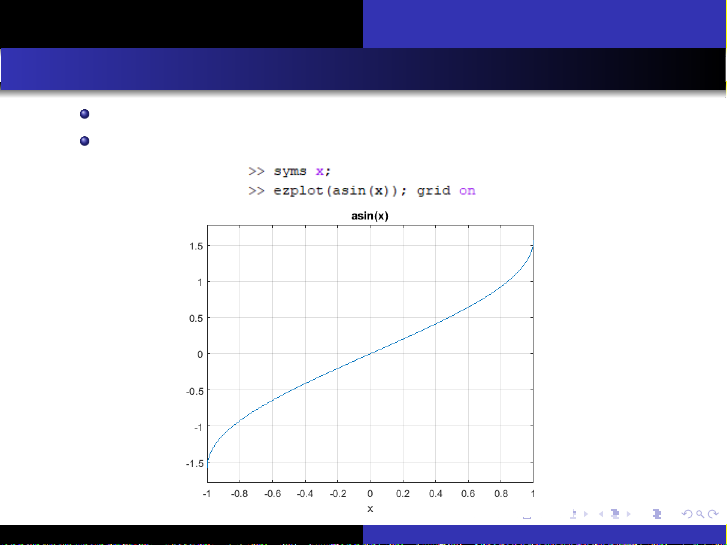
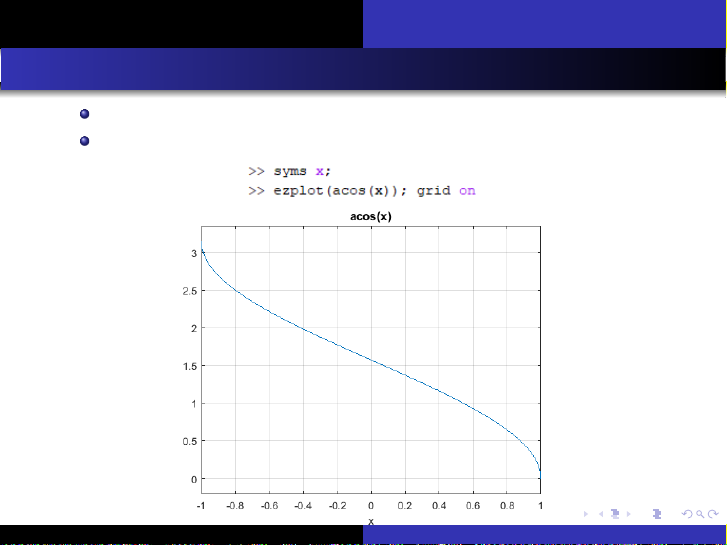
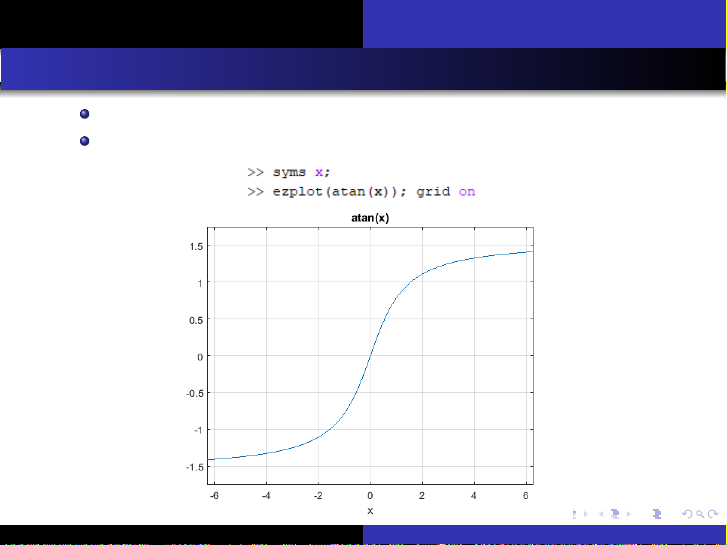
Tài liệu này trình bày chi tiết các nội dung cốt lõi của môn Giải tích 1, bắt đầu với việc giới thiệu các hàm số lượng giác ngược như arcsin x, arccos x và arctan x. Đối với mỗi hàm, tài liệu định nghĩa rõ ràng, chỉ ra tập xác định và tập giá trị, đồng thời minh họa bằng đồ thị để người đọc dễ hình dung. Tiếp theo, tài liệu đi sâu vào các hàm số hyperbolic bao gồm sinh x, cosh x, tanh x và coth x, cung cấp định nghĩa, công thức tính toán, và phân tích các đặc trưng về tập xác định, tập giá trị qua các biểu đồ trực quan. Phần cuối cùng tập trung vào khái niệm giới hạn của hàm số, một nền tảng quan trọng trong giải tích. Tài liệu giới thiệu định nghĩa giới hạn theo epsilon-delta, đồng thời đề cập đến các khái niệm liên quan như các giới hạn cơ bản, đại lượng vô cùng bé và đại lượng vô cùng lớn, giúp người học xây dựng nền tảng vững chắc cho các chủ đề giải tích nâng cao.