PGS.TS. Phan Huy Kh
PGS.TS. Phan Huy Khá
ánh
nh
khanhph@vnn.vn
khanhph@vnn.vn
H
Hệ
ệ
chuyên gia
chuyên gia
(
(Expert System
Expert System)
)
Chương 2
Biểu diễn tri thức
nhờ
logic vị
từ
bậc một
2.3
2/
2/69
69
Chương
Chương 2
2
Bi
Biể
ểu di
u diễ
ễn tri th
n tri thứ
ức nh
c nhờ
ờ
logic v
logic vị
ị
t
từ
ừ
b
bậ
ậc m
c mộ
ột
t
a
aPh
Phầ
ần 2.3 :
n 2.3 :
V
VLôgic v
Lôgic vị
ịt
từ
ừb
bậ
ậc m
c mộ
ột
t
V
VBi
Biể
ểu di
u diễ
ễn tri th
n tri thứ
ức nh
c nhờ
ờlogic v
logic vị
ịt
từ
ừb
bậ
ậc m
c mộ
ột
t
3/
3/69
69
Limitations of Propositional Logic 2
Limitations of Propositional Logic 2
a
aCan't directly talk about properties of individuals
Can't directly talk about properties of individuals
or relations between individuals
or relations between individuals
V
VE.g.,
E.g., how to represent the fact that John is tall?
how to represent the fact that John is tall?
a
aWe have no way to conclude that
We have no way to conclude that John is good at
John is good at
basketball
basketball!
!
a
aGeneralizations, patterns, regularities can't easily be
Generalizations, patterns, regularities can't easily be
represented
represented
V
VE.g.,
E.g., all triangles have 3 sides
all triangles have 3 sides
4/
4/69
69
Predicate Logic Overview
Predicate Logic Overview
a
aPredicate Logic
Predicate Logic
V
VPrinciples
Principles
V
VObjects
Objects
V
VRelations
Relations
V
Vproperties
properties
a
aSyntax
Syntax
a
aSemantics
Semantics
a
aExtensions and Variations
Extensions and Variations
a
aProof in Predicate Logic
Proof in Predicate Logic
a
aImportant
Important Concepts and Terms
Concepts and Terms
5/
5/69
69
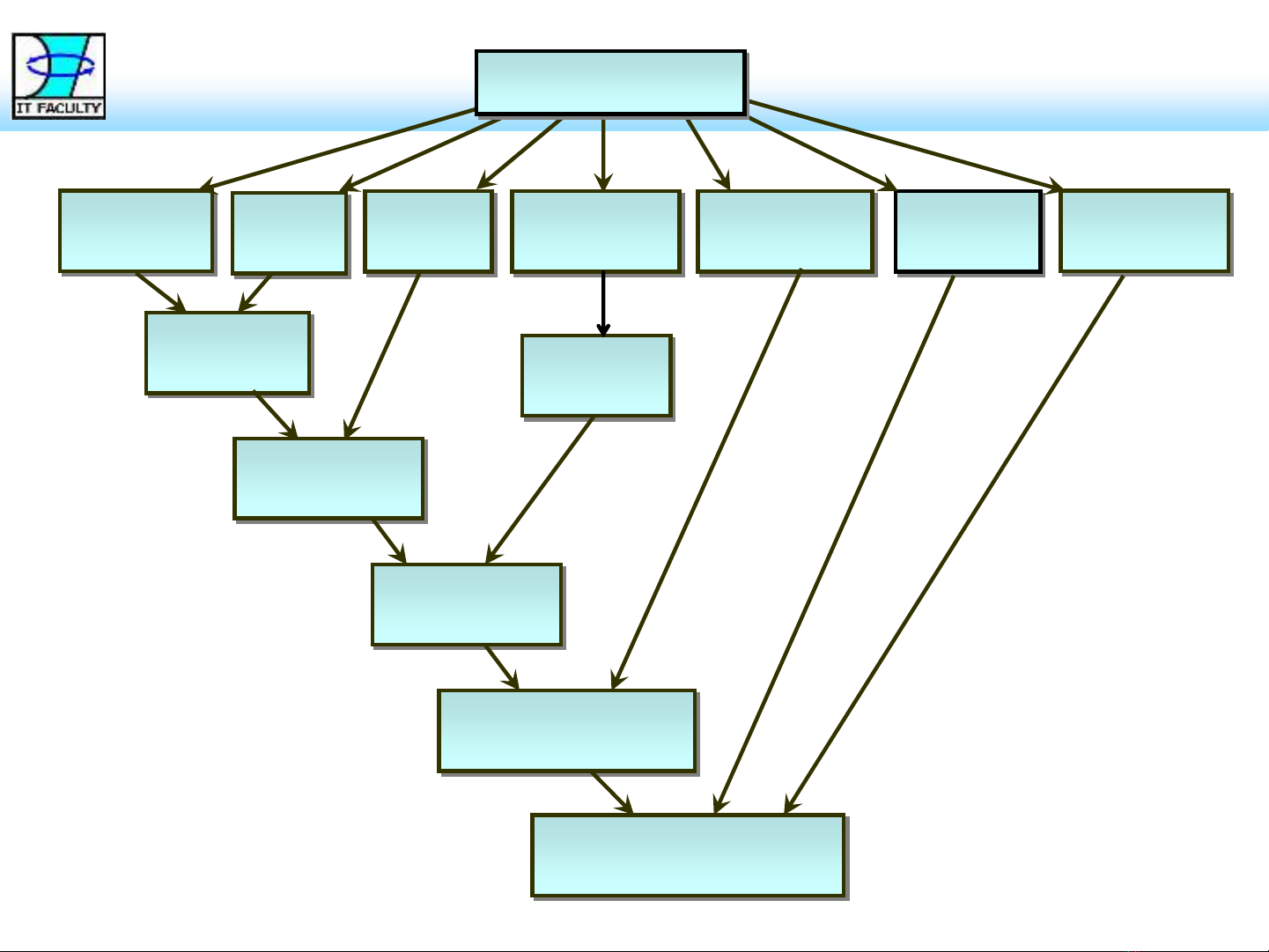
Delimiters
, ( )
Delimiters
, ( )
Constants
a..z
Constants
a..z Variale
A..Z
Variale
A..Z Function
f g h
Function
f g h Predicate
P0
P Q R
Predicate
P0
P Q R Connective
¬∧∨→↔
Connective
¬∧∨→↔
Quantifier
∀∃
Quantifier
∀∃
Term
ti
Term
ti
Term
f(t1
, …tn
)
Term
f(t1
, …tn
)
Atom
P Q R
Atom
P Q R
Atom
P(t1
, …tn
)
Atom
P(t1
, …tn
)
Wff
P∧
Q →
R
Wff
P∧
Q →
R
Wff
∃X ∀Y (P(X, Y) →
R(Y))
Wff
∃X ∀Y (P(X, Y) →
R(Y))
Alphabet
Alphabet